bzoj 4321 queue2 dp

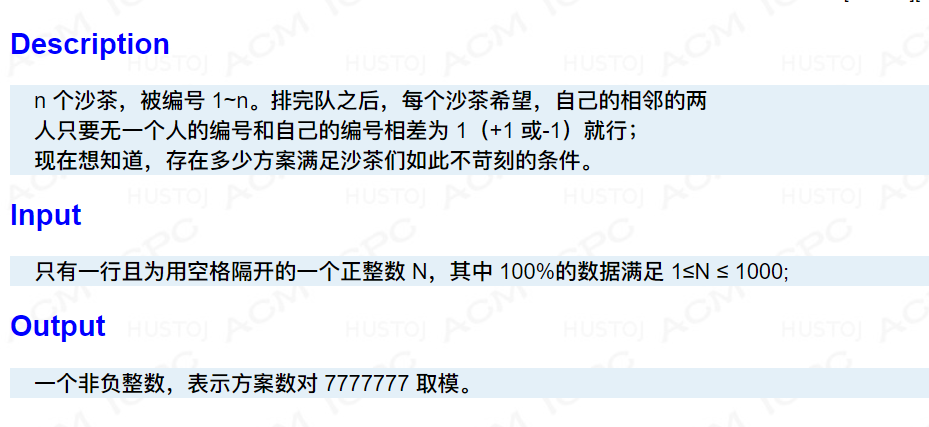
简单$dp$，考虑从大到小插入

设个状态$f[i][j][0 / 1]$表示$i$和$i - 1$是否相邻即可

转移看代码就能看懂吧...

复杂度$O(n^2)$

#include <set>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
namespace remoon {
    #define ri register int
    #define rep(iu, st, ed) for(ri iu = st; iu <= ed; iu ++)
    #define drep(iu, ed, st) for(ri iu = ed; iu >= st; iu --)    
    #define gc getchar
    inline int read() {
        int p = 0, w = 1; char c = gc();
        while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); }
        while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc();
        return p * w;
    }
    int wr[50], rw;
    #define pc(iw) putchar(iw)
    tpr inline void write(ra o, char c = '\n') {
        if(!o) pc('0');
        if(o < 0) o = -o, pc('-');
        while(o) wr[++ rw] = o % 10, o /= 10;
        while(rw) pc(wr[rw --] + '0');
        pc(c);
    }
}
using namespace std;
using namespace remoon;

namespace mod_mod {
    #define mod 7777777
    inline void inc(int &a, int b) { a += b; if(a >= mod) a -= mod; }
    inline void dec(int &a, int b) { a -= b; if(a < 0) a += mod; }
    inline int Inc(int a, int b) { return (a + b >= mod) ? a + b - mod : a + b; }
    inline int Dec(int a, int b) { return (a - b < 0) ? a - b + mod : a - b; }
    inline int mul(int a, int b) { return 1ll * a * b % mod; }
}
using namespace mod_mod;

#define sid 1005
int n;
int f[sid][sid][2];

int main() {
    n = read();
    f[1][0][0] = 1;
    rep(i, 0, n) rep(j, 0, i - 1) {
        
        inc(f[i + 1][j][0], mul(f[i][j][0], i - j - 1));
        if(j) inc(f[i + 1][j - 1][0], mul(f[i][j][0], j));
        inc(f[i + 1][j + 1][1], mul(f[i][j][0], 2));
        
        inc(f[i + 1][j][1], f[i][j][1]);
        inc(f[i + 1][j + 1][1], f[i][j][1]);
        inc(f[i + 1][j][0], mul(f[i][j][1], i - j));
        if(j) inc(f[i + 1][j - 1][0], mul(f[i][j][1], j - 1));

    }
    write(f[n][0][0]);
    return 0;
}

 

打表可$O(1)$