P1354 房间最短路问题

题目链接

思路：

​ 看到此题，第一个想到的是贪心：要从(0.0,5.0)走到(10.0,5.0),就要绕过一些墙,那就会经过一些墙的端点(下文称之为节点),单从样例看来,就会说走到离当前节点距离最小的点就行了,但真的是这样吗?

​ 显然不是,原因有二:

1. 如果起点到终点没有障碍,那么走其它节点是不是就会走了冗余的路?是的,在某些最优方案中,确实会出现从间隙中穿过的情况.

2. 即使没有出现上述情况,试观察下图,贪心的路径为红色,正解为蓝色.

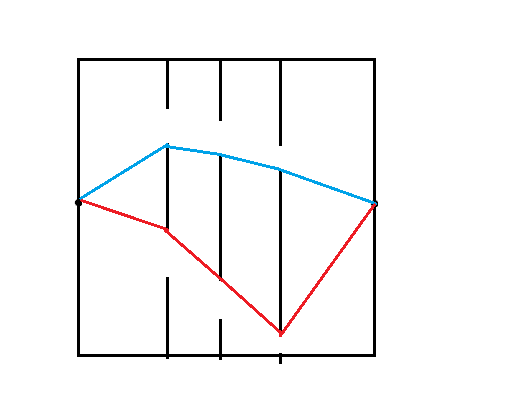
​ 这个贪心思路看来是不行了,但它带给我们一些小提示:路径可能会穿过某堵墙空隙而非落在这堵墙的节点上;路径中只存在线段且每条线段的两端都是落在节点上的,换种说法就是路径只会在节点拐弯.(想想为什么?戳我看解答)

​ 既然数据范围\(n\le20\),那么考虑暴力如何?

​ 于是很快想到了暴力流程:

1. 从起点(0.0,5.0)出发并作为当前节点;
2. 对于当前节点u,遍历下一个要到达的节点v,判断它能否到达
   1. 如果能够到达,那么跳到v,将v作为u进行下一轮dfs.
   2. 如果不能到达,考虑下一个点.
3. 如果遇到终点则记录路径然后回溯重复上一步骤.

明确了思路后,就开始编代码吧.

历程:

暴力代码段打出来如下:

_{(为了突出被执行语段,注释与背景主题近色,如需查看,请选中语段或者放入IDE)}

double dis(double x1,double y1,double x2,double y2){//两点距离
	return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
bool check(int u,int v,double x1,double y1,double x2,double y2){//判断是否可达,若可达,则返回值为1,否则为0
	double kk=(y1-y2)/(x1-x2);
	double bb=y1-kk*x1;
    /*y=kx+b*/
	for(int i=u+1;i<v;i++){
		double sth=kk*w[i][0]+bb;
		if(!((w[i][1]<=sth&&sth<=w[i][2])||(w[i][3]<=sth&&sth<=w[i][4])))return 0;//如果被挡住了
	}
	return 1;
}
void dfs(int u,double yy,double cost){
	if(u==n+1){//终点的墙编号为n+1
		ans=min(ans,cost);
		return ;
	}
	for(int v=u+1;v<=n+1;v++){
		if(u!=n){
			for(int i=1;i<=4;i++){
				if(check(u,v,w[u][0],yy,w[v][0],w[v][i])){
					dfs(v,w[v][i],cost+dis(w[u][0],yy,w[v][0],w[v][i]));
				}
			}
		}else{
			if(check(u,v,w[u][0],yy,10.0,5.0)){//终点特判一下,提高效率
				dfs(n+1,5.0,cost+dis(w[u][0],yy,10.0,5.0));
			}
		}
	}
}

放进题目写出来是这样的(注释的语段为调试功能):

_{(为了突出被执行语段,注释与背景主题近色,如需查看,请选中语段或者放入IDE)}

#include <bits/stdc++.h>
using namespace std;
int n;
double ans=99999999.0;
double w[30][5];
double dis(double x1,double y1,double x2,double y2){
	return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
bool check(int u,int v,double x1,double y1,double x2,double y2){
	double kk=(y1-y2)/(x1-x2);
	double bb=y1-kk*x1;
	for(int i=u+1;i<v;i++){
		double sth=kk*w[i][0]+bb;
//		cout<<i<<endl;
//		for(int j=0;j<=4;j++)printf("%g ",w[i][j]);
//		puts("");
//		printf("%g ",w[v][0]);
//		cout<<' '<<i<<endl;
//		cout<<(w[i][1]<=sth&&sth<=w[i][2]);
		if(!((w[i][1]<=sth&&sth<=w[i][2])||(w[i][3]<=sth&&sth<=w[i][4])))return 0;
	}
	return 1;
}
void dfs(int u,double yy,double cost){
//	printf("%d %g\n",u,yy);
//	getchar();
	if(u==n+1){
		ans=min(ans,cost);
		return ;
	}
	for(int v=u+1;v<=n+1;v++){
		if(u!=n){
			for(int i=1;i<=4;i++){
				if(check(u,v,w[u][0],yy,w[v][0],w[v][i])){
					dfs(v,w[v][i],cost+dis(w[u][0],yy,w[v][0],w[v][i]));
				}
			}
		}else{
			if(check(u,v,w[u][0],yy,10.0,5.0)){
				dfs(n+1,5.0,cost+dis(w[u][0],yy,10.0,5.0));
			}
		}
	}
}
int main() {
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=4;j++)cin>>w[i][j];
	}
	/*
	for(int i=1;i<=n;i++){
		for(int j=0;j<=4;j++)printf("%g ",w[i][j]);
		puts("");
	}
	*/
//	cout<<check(0,2,0.0,5.0,7.0,4.5)<<endl;
	w[0][0]=0.0;
	w[n+1][0]=10.0;
	for(int i=1;i<=4;i++)w[0][i]=5.0,w[n+1][i]=5.0;
	dfs(0,5.0,0.0);
	printf("%.2lf",ans);
	return 0;
}

作为暴力,还是超时了,能拿到80分(还是不错了),

​

​ 这时候就要用上暴力的救星——记忆化了,令\(f_{i,j}\)表示到达第i堵墙的第j个节点所用的最小距离,那么只要当前路径超过这个值自然是走不下去的了,将其放进代码中优化一下就AC了:

AC💯代码(注释语段为调试功能):

_{(为了突出被执行语段,注释与背景主题近色,如需查看,请选中语段或者放入IDE)}

#include <bits/stdc++.h>
using namespace std;
int n;
double ans=99999999.0;
double w[30][5],f[30][5];
double dis(double x1,double y1,double x2,double y2){
	return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
bool check(int u,int v,double x1,double y1,double x2,double y2){
	double kk=(y1-y2)/(x1-x2);
	double bb=y1-kk*x1;
	for(int i=u+1;i<v;i++){
		double sth=kk*w[i][0]+bb;
//		cout<<i<<endl;
//		for(int j=0;j<=4;j++)printf("%g ",w[i][j]);
//		puts("");
//		printf("%g ",w[v][0]);
//		cout<<' '<<i<<endl;
//		cout<<(w[i][1]<=sth&&sth<=w[i][2]);
		if(!((w[i][1]<=sth&&sth<=w[i][2])||(w[i][3]<=sth&&sth<=w[i][4])))return 0;
	}
	return 1;
}
void dfs(int u,int u2,double cost){
	double yy=w[u][u2];
	if(cost>f[u][u2])return ;
	f[u][u2]=cost;
//	printf("%d %g\n",u,yy);
//	getchar();
	if(u==n+1){
		ans=min(ans,cost);
		return ;
	}
	for(int v=u+1;v<=n+1;v++){
		if(u!=n){
			for(int i=1;i<=4;i++){
				if(check(u,v,w[u][0],yy,w[v][0],w[v][i])){
					dfs(v,i,cost+dis(w[u][0],yy,w[v][0],w[v][i]));
				}
			}
		}else{
			if(check(u,v,w[u][0],yy,10.0,5.0)){
				dfs(n+1,1,cost+dis(w[u][0],yy,10.0,5.0));
			}
		}
	}
}
int main() {
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=4;j++)cin>>w[i][j],f[i][j]=99999999.0;
	}
	for(int i=1;i<=n+1;i++){
		for(int j=0;j<=4;j++)f[i][j]=99999999.0;
	}
	/*
	for(int i=1;i<=n;i++){
		for(int j=0;j<=4;j++)printf("%g ",w[i][j]);
		puts("");
	}
	*/
//	cout<<check(0,2,0.0,5.0,7.0,4.5)<<endl;
	w[0][0]=0.0;
	w[n+1][0]=10.0;
	for(int i=1;i<=4;i++)w[0][i]=5.0,w[n+1][i]=5.0;
	dfs(0,1,0.0);
	printf("%.2lf",ans);
	return 0;
}

大功告成!

​ 后记:这道题不止暴力一个做法,但暴力是最容易想出来的,暴力的优化也更是不止记忆化,还可以看看其它更为优秀的算法.