LeetCode98. 验证二叉搜索树

 验证二叉搜索树

 *

 * https://leetcode-cn.com/problems/validate-binary-search-tree/description/

 *

 * algorithms

 * Medium (27.95%)

 * Likes:    340

 * Dislikes: 0

 * Total Accepted:    53K

 * Total Submissions: 189.7K

 * Testcase Example:  '[2,1,3]'

 *

 * 给定一个二叉树，判断其是否是一个有效的二叉搜索树。

 * 

 * 假设一个二叉搜索树具有如下特征：

 * 

 * 

 * 节点的左子树只包含小于当前节点的数。

 * 节点的右子树只包含大于当前节点的数。

 * 所有左子树和右子树自身必须也是二叉搜索树。

 * 

 * 

 * 示例 1:

 * 

 * 输入:

 * ⁠   2

 * ⁠  / \

 * ⁠ 1   3

 * 输出: true

 * 

 * 

 * 示例 2:

 * 

 * 输入:

 * ⁠   5

 * ⁠  / \

 * ⁠ 1   4

 * / \

 * 3   6

 * 输出: false

 * 解释: 输入为: [5,1,4,null,null,3,6]。

 * 根节点的值为 5 ，但是其右子节点值为 4 。

 * 

 * 

 */

根据二叉搜索树的定义 其中序遍历是递增的

//中序遍历
class Solution {
public:
    TreeNode* pre;
    bool isValidBST(TreeNode* root) {
        if(!root) return true;
        stack<TreeNode*>ss;
        TreeNode* cur=root;
        while(ss.size()||cur)
        {
            while (cur)
            {
                ss.push(cur);
                cur=cur->left;
            }
            cur=ss.top();
            ss.pop();
            if(pre&&pre->val >= cur->val) return false;
            pre=cur;
            cur=cur->right;
        }
        return true;
        
    }
};

//递归我是真的想不开啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
//啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
//啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
//啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
class Solution{
private:
     bool anotherBST(TreeNode* root,int* lower,int* upper)
     {
          if(root==NULL) return true;
          if(lower!=NULL&&root->val<=(*lower)) return false;
          if(upper!=NULL&&root->val>=(*upper)) return false;
          if(!anotherBST(root->left,lower,&(root->val))) return false;
          if(!anotherBST(root->right,&(root->val),upper)) return false;
          return true;
     }

public:
     bool isValidBST(TreeNode* root)
          {
               return anotherBST(root,NULL,NULL);
          }
};

直觉
乍一看，这是一个平凡的问题。只需要遍历整棵树，检查 node.right.val > node.val 和
node.left.val < node.val 对每个结点是否成立。

 

 

 

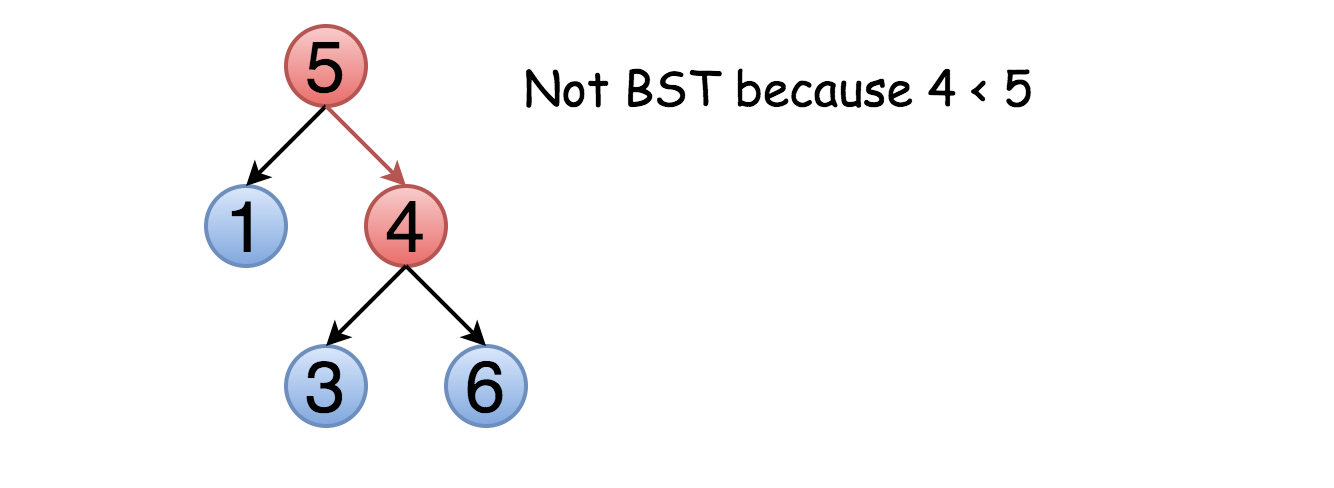
问题是，这种方法并不总是正确。不仅右子结点要大于该节点，整个右子树的元素都应该大于该节点。例如:

 

这意味着我们需要在遍历树的同时保留结点的上界与下界，在比较时不仅比较子结点的值，也要与上下界比较。

 

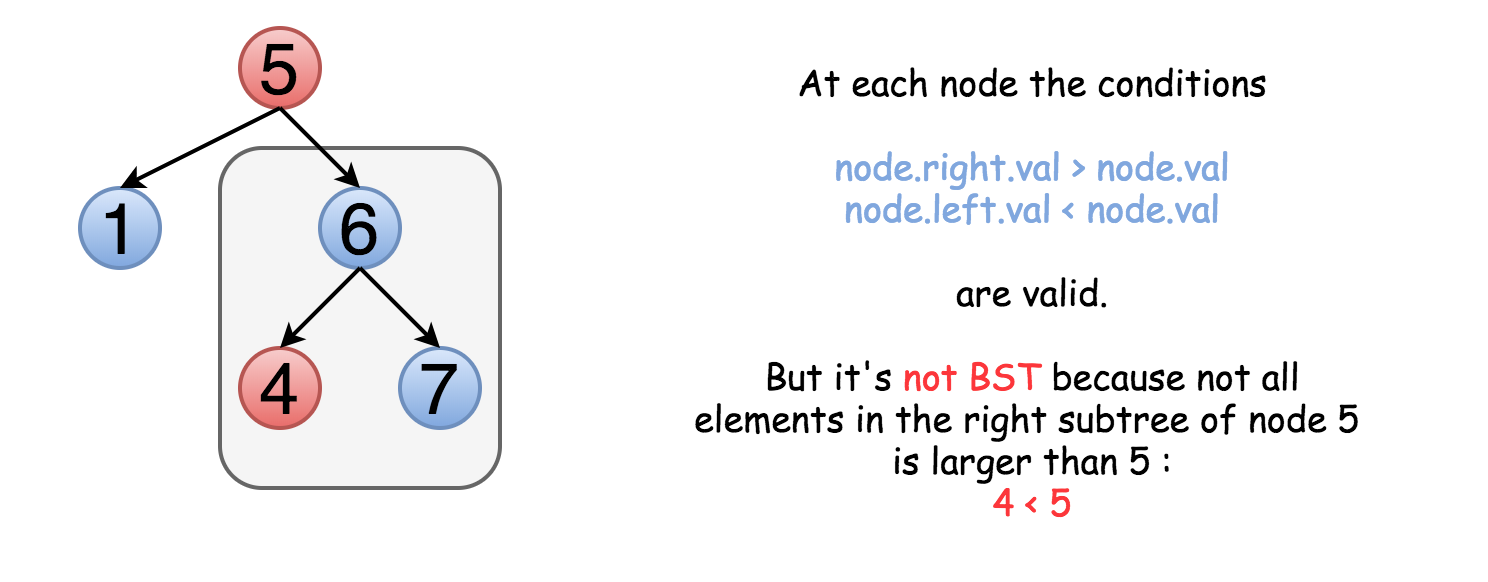
 代码就是上面的递归方式，，在子树是否为二叉树的判定中，*low和*up是不同的值。如上图 遍历到4时，其lower是5，upper是6