二叉搜索树

二叉搜索树是二叉树的一种特殊形式。 二叉搜索树具有以下性质：每个节点中的值必须大于（或等于）其左侧子树中的任何值，但小于（或等于）其右侧子树中的任何值。

二叉搜索树的定义

---

二叉搜索树（BST）是二叉树的一种特殊表示形式，它满足如下特性：

1. 每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
2. 每个节点中的值必须小于（或等于）存储在其右子树中的任何值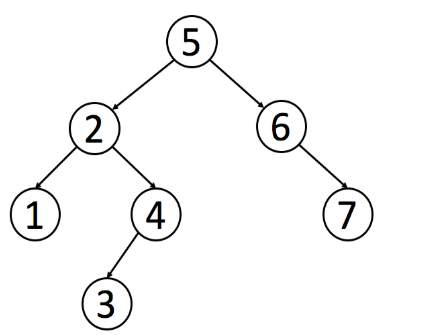
3. 
4.  对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。因此，中序遍历是二叉搜索树中最常用的遍历方法。可以通过中序遍历来找到二叉搜索树的中序后继节点
5.  在二叉搜索树中实现搜索操作

   ---

   二叉搜索树主要支持三个操作：搜索、插入和删除。

   根据BST的特性，对于每个节点：

   1. 如果目标值等于节点的值，则返回节点;
   2. 如果目标值小于节点的值，则继续在左子树中搜索;
   3. 如果目标值大于节点的值，则继续在右子树中搜索。

   可以运用递归或迭代方法去解决这类问题

    

    

    在二叉搜索树中实现插入操作 - 介绍

    

   二叉搜索树中的另一个常见操作是插入一个新节点。有许多不同的方法去插入新节点，这篇文章中，我们只讨论一种使整体操作变化最小的经典方法。 它的主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。 因此，搜索将成为插入的起始。

   与搜索操作类似，对于每个节点，我们将：

   1. 根据节点值与目标节点值的关系，搜索左子树或右子树；
   2. 重复步骤 1 直到到达外部节点；
   3. 根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

   这样，我们就可以添加一个新的节点并依旧维持二叉搜索树的性质。

   与搜索操作相同，我们可以递归或迭代地进行插入。 它的解决方案也与搜索非常相似

    

   在二叉搜索树中实现删除操作

   ---

   删除要比我们前面提到过的两种操作复杂许多。有许多不同的删除节点的方法，这篇文章中，我们只讨论一种使整体操作变化最小的方法。我们的方案是用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数，我们需考虑以下三种情况：

   1. 如果目标节点没有子节点，我们可以直接移除该目标节点。
   2. 如果目标节只有一个子节点，我们可以用其子节点作为替换。
   3. 如果目标节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该目标节点。

   我们来看下面这几个例子，以帮助你理解删除操作的中心思想：

    

   例 1：目标节点没有子节点

    

    

    

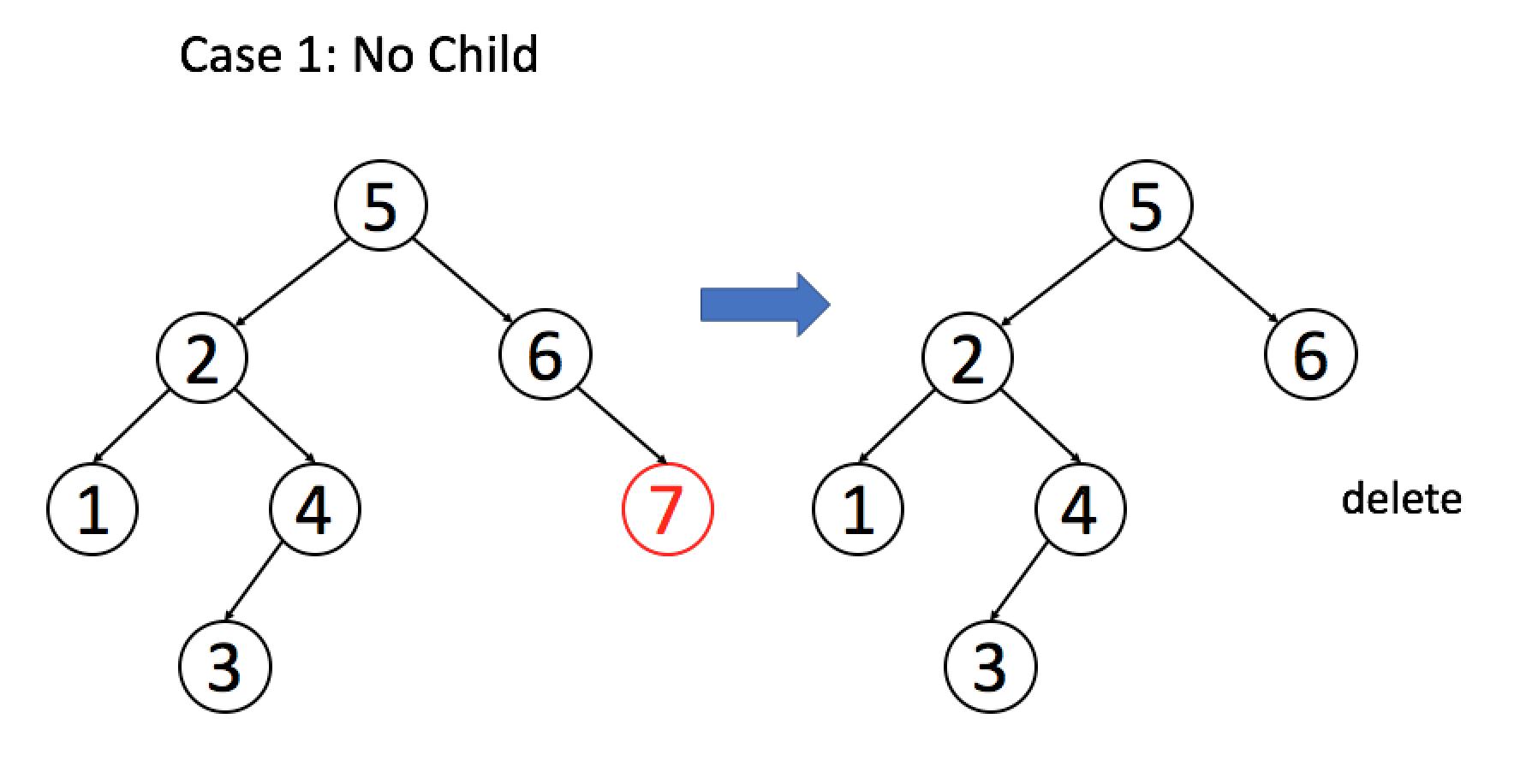
   例 2：目标节只有一个子节点

    

    

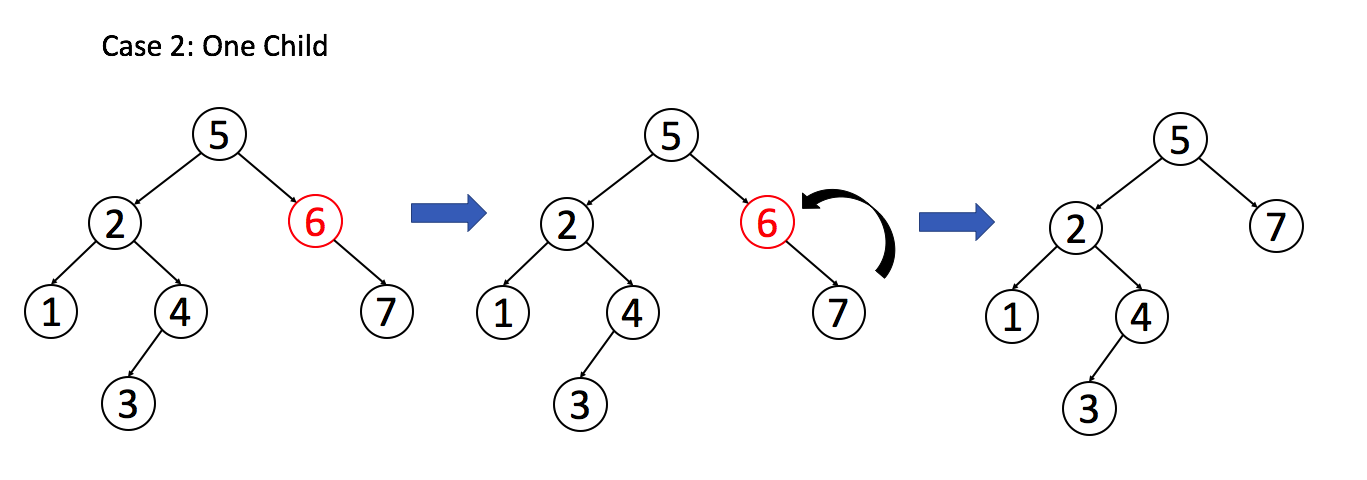
    例 3：目标节点有两个子节点

   

    

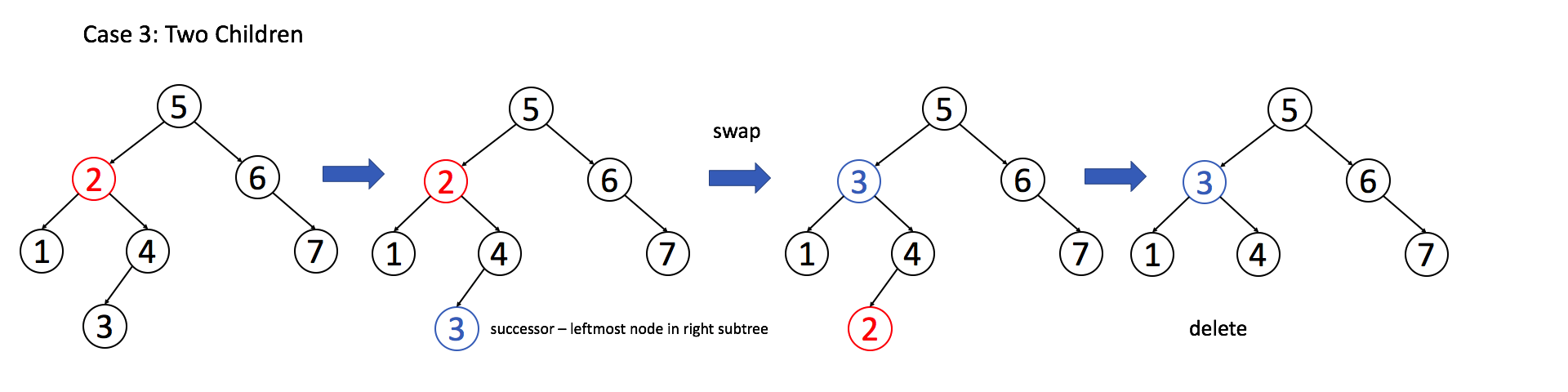
   什么是一个高度平衡的二叉搜索树?

   ---

   树结构中的常见用语:

   • 节点的深度 - 从树的根节点到该节点的边数
   • 节点的高度 - 该节点和叶子之间最长路径上的边数
   • 树的高度 - 其根节点的高度

   一个高度平衡的二叉搜索树（平衡二叉搜索树）是在插入和删除任何节点之后，可以自动保持其高度最小。也就是说，有N个节点的平衡二叉搜索树，它的高度是logN。并且，每个节点的两个子树的高度不会相差超过1。

   为什么是logN呢?

   • 一个高度为h的二叉树 .
   • 换言之，一个有N个节点，且高度为h的二叉树: .
   • 所以： .

   下面是一个普通二叉搜索树和一个高度平衡的二叉搜索树的例子:

   

   根据定义, 我们可以判断出一个二叉搜索树是否是高度平衡的 (平衡二叉树)。

   正如我们之前提到的, 一个有N个节点的平衡二搜索叉树的高度总是logN。因此，我们可以计算节点总数和树的高度，以确定这个二叉搜索树是否为高度平衡的。

   同样，在定义中， 我们提到了高度平衡的二叉树一个特性: 每个节点的两个子树的深度不会相差超过1。我们也可以根据这个性质，递归地验证树

    

   为什么需要用到高度平衡的二叉搜索树?

   ---

   我们已经介绍过了二叉树及其相关操作, 包括搜索、插入、删除。 当分析这些操作的时间复杂度时，我们需要注意的是树的高度是十分重要的考量因素。以搜索操作为例，如果二叉搜索树的高度为h，则时间复杂度为O(h)。二叉搜索树的高度的确很重要。

   所以，我们来讨论一下树的节点总数N和高度h之间的关系。 对于一个平衡二叉搜索树, 我们已经在前文中提过,  。但对于一个普通的二叉搜索树， 在最坏的情况下, 它可以退化成一个链。

   因此，具有N个节点的二叉搜索树的高度在logN到N区间变化。也就是说，搜索操作的时间复杂度可以从logN变化到N。这是一个巨大的性能差异。

   所以说，高度平衡的二叉搜索树对提高性能起着重要作用。

   如何实现一个高度平衡的二叉搜索树?

   ---

   有许多不同的方法可以实现。尽管这些实现方法的细节有所不同，但他们有相同的目标:

   1. 采用的数据结构应该满足二分查找属性和高度平衡属性。
   2. 采用的数据结构应该支持二叉搜索树的基本操作，包括在O(logN)时间内的搜索、插入和删除，即使在最坏的情况下也是如此。

   我们提供了一个常见的的高度平衡二叉树列表供您参考：

   • 红黑树
   • AVL树
   • 伸展树
   • 树堆

     高度平衡的二叉搜索树的实际应用

     ---

     高度平衡的二叉搜索树在实际中被广泛使用，因为它可以在O(logN)时间复杂度内执行所有搜索、插入和删除操作。

     平衡二叉搜索树的概念经常运用在Set和Map中。 Set和Map的原理相似。 我们将在下文中重点讨论Set这个数据结构。

     Set(集合)是另一种数据结构，它可以存储大量key(键)而不需要任何特定的顺序或任何重复的元素。 它应该支持的基本操作是将新元素插入到Set中，并检查元素是否存在于其中。

     通常，有两种最广泛使用的集合：散列集合(Hash Set)和树集合(Tree Set)。

     树集合, Java中的Treeset或者C++中的set，是由高度平衡的二叉搜索树实现的。因此，搜索、插入和删除的时间复杂度都是O(logN)。

     散列集合, Java中的HashSet或者C++中的unordered_set，是由哈希实现的, 但是平衡二叉搜索树也起到了至关重要的作用。当存在具有相同哈希键的元素过多时，将花费O(N)时间复杂度来查找特定元素，其中N是具有相同哈希键的元素的数量。 通常情况下，使用高度平衡的二叉搜索树将把时间复杂度从 O(N) 改善到 O(logN)。

     哈希集和树集之间的本质区别在于树集中的键是有序的。