【HAOI2011】 Problem b（数论函数+卷积）

 

【HAOI2011】 Problem b

题目描述

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

输入格式

第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

输出格式

共n行，每行一个整数表示满足要求的数对(x,y)的个数

说明/提示

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

【解题思路】

 可以将所求的值简化为下方公式：

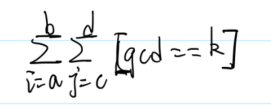
推导过程如下：

先将（i，j）==k，同时给范围和值除以k，得到，（i，j）==1就非常好处理，互质

用元函数代换掉条件表达式，利用狄利克雷卷积代换

然后枚举d，同时将gcd进行转化，当d能够同时被i，j整除（图里写错了，应该是（i%d）==0，（j%d）==0，orz）时条件成立

所以就能够再次对i，j范围进行缩减，这样就能够得到图中右下的公式

通过数论整除和埃筛就能够快速求到1~n和1~m范围内的值的总和

 

然后利用二维空间上的容斥思想，减去重复部分

得到最终答案