算法学习：半平面交

【定义】

【半平面交】多条直线的同一方向的区域所围成的区域，参考数学中的线性规划

（图咕了）

【内核】形象的说就是在多边形中可以找到一个区域安放一台360°摄像头，能够监视到整个凸多边形区域

抽象的来说，就是在这个区域中任意一点以任意方向做直线，都能够在不和多边形边相交的情况下，达到多边形中任意一点

【半平面交】

在网上博客中，我们能找到一种n^2的算法

枚举所有的边，在枚举所有的点

如果某个点在之前枚举的边之内的话，就说明这个点能够使面积缩小

然后求这个点和周围两个点形成的新直线和周围两个点形成的直线的交点

逐渐缩小范围

通过这个过程我们能够想到，求半平面交的过程能够看成一个切蛋糕的过程

每一次切的过程，去掉一些不符合要求的交点，最终得到半平面交的所有节点

为了降低时间复杂度，我们尝试观察每次切的时候的两两直线交点特性

我们会发现，我们按照极角排序，不停的切割时

每次满足条件的节点总是连续的一段，不符合的节点也是连续的

满足的在中间，不满足的在两端

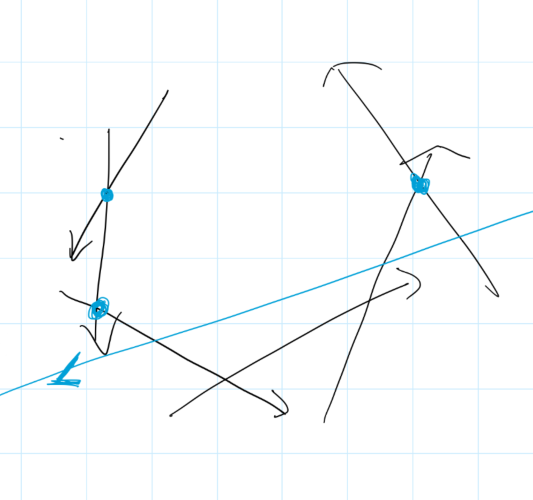
下图黑色是已经得到的半平面交，蓝色是切割的

所以我们用一个双端队列保存所有交点，每次切的时候就判断两端，排除不符合条件的交点

然后在两端再加上新的直线和两端直线的交点

而这里既然需要求直线的交点，那我们就不止需要一个双端队列了

我们还需要另外一个双端队列保存满足条件的直线，和弹出交点的时候，同时弹出对应直线

最终结束的时候，因为写的判定只是在排除极角小于/大于的直线

而最开始的直线并没有判断，所以需要再进行一次判断，去掉所有不符合条件的点

最终才能获得正确答案

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps  = 1e-6;
const int    MAXN = 20010;
const double lim  = 10000;
const double PI   = acos(-1.0);
int n, m;
inline int cmp(double x)
{
    if (x > eps)return 1;
    return x < -eps ? -1 : 0;
}
struct V
{
    double x, y;
    double ang;
    double angle()
    {//求取极角
        return atan2(y, x);
    }
    V(double X = 0, double Y = 0)
    {
        //初始化
        x = X, y = Y;
        ang = atan2(y, x);
    }
    bool operator ==(const V &b)
    {
        return cmp(x-b.x)&&cmp(y-b.y);
    }
    
};
typedef V  P;
V operator +(V a, V b) { return V(a.x + b.x, a.y + b.y); }
V operator -(V a, V b) { return V(a.x - b.x, a.y - b.y); }
V operator *(V a, double b) { return V(a.x *b, a.y*b ); }
V operator /(V a, double b) { return V(a.x /b, a.y/b ); }
struct L
{
    P s, t;
    double ang;
    L(P X = V(), P Y = V())
    {
        s = X, t = Y, ang = (Y - X).angle();
    }
};
typedef L S;
double cross(V a, V b)
{
    return a.x*b.y - a.y*b.x;
}
bool operator <(const L &a, const L &b)
{
    double r = a.ang - b.ang;
    if (cmp(r) != 0)    return cmp(r) == -1;
    //极角相同，默认偏下的更大
    return cmp(cross(a.t - a.s, b.t - a.s)) == -1;
}
double dot(V a, V b)
{
    return a.x*b.x + a.y*b.y;
}
bool is_parallel(L a, L b)
{
    return cmp(cross(a.t - a.s, b.t - b.s)) == 0;
}
P intersection(L a, L b)
{
    return a.s + (a.t - a.s)*(cross(b.t - b.s, a.s-b.s)) / cross(a.t - a.s, b.t - b.s);
}
double area(P *p, int n)
{
    double res = 0;
    p[n + 1] = p[1];
    for (int i = 1; i <= n; i++)
        res += cross(p[i], p[i + 1]);
    return fabs(res / 2);
}
bool is_right(L a, P b)
//判断点b是否在直线的右边（和起点连成的向量方向和直线向量方向相反）
{
    return cmp(cross(a.t - a.s, b - a.s)) < 0;
}
bool SI(L *l, int n, P *s, int &m)
//增量法求半平面交
{
    static L que[MAXN];
    static P que2[MAXN];
    int head = 0, tail = 0;
    sort(l + 1, l + 1 + n);
    que[head]=l[1];
    for (int i = 2; i <= n; i++)
    {
        if (cmp(l[i].ang - l[i - 1].ang))
        {
            if (head<tail && (is_parallel(que[head], que[head + 1]) || is_parallel(que[tail], que[tail - 1])))
            //若两个直线共线，但是极角不同，则没有半平面交
                return false;
            while (head < tail&&is_right(l[i], que2[tail - 1])) tail--;
            while (head < tail&&is_right(l[i], que2[head    ])) head++;
            que[++tail] = l[i];
            if (head < tail) 
                que2[tail - 1] = intersection(que[tail],que[tail-1]);
        }
    }
    while (head < tail&&is_right(que[head], que2[tail-1])) tail--;
    while (head < tail&&is_right(que[tail], que2[head  ])) head++;
    if (tail - head <= 1) return false;
    que2[tail] = intersection(que[head], que[tail]);
    m = 0;
    for (int i = head; i <= tail; i++)
        s[++m] = que2[i];
    return true;
}
P p[MAXN];
L l[MAXN];
double solve()
//求取半平面交的面积
//SI函数计算结果只是得到了半平面交的多边形数组
{
    P a = P(0, 0), b = P(lim, 0), c = P(lim, lim), d = P(0, lim);
    l[++n] = L(a, b);
    l[++n] = L(b, c);
    l[++n] = L(c, d);
    l[++n] = L(d, a);
    if (!SI(l, n, p, m))
        return 0;
    return area(p, m);
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        P a, b;
        scanf("%lf%lf%lf%lf", &a.x, &a.y, &b.x, &b.y);
        //直线方向，从起点指向终点
        //向量表示，终点减去起点
        l[i] = L(a, b);
    }
    printf("%.1f", solve());
    return 0;
}

View Code

【模板题】

【CQOI2006】凸多边形

裸题，可测模板

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<vector>
  4 #include<queue>
  5 #include<iostream>
  6 #include<algorithm>
  7 #include<cmath>
  8 using namespace std;
  9 const double eps = 1e-6;
 10 const int    MAXN = 20010;
 11 const double lim = 10000;
 12 const double PI = acos(-1.0);
 13 int n, m;
 14 inline int cmp(double x)
 15 {
 16     if (x > eps)return 1;
 17     return x < -eps ? -1 : 0;
 18 }
 19 struct V
 20 {
 21     double x, y;
 22     double ang;
 23     double angle()
 24     {//求取极角
 25         return atan2(y, x);
 26     }
 27     V(double X = 0, double Y = 0)
 28     {
 29         //初始化
 30         x = X, y = Y;
 31         ang = atan2(y, x);
 32     }
 33     bool operator ==(const V &b)
 34     {
 35         return cmp(x - b.x) && cmp(y - b.y);
 36     }
 37 
 38 };
 39 typedef V  P;
 40 V operator +(V a, V b) { return V(a.x + b.x, a.y + b.y); }
 41 V operator -(V a, V b) { return V(a.x - b.x, a.y - b.y); }
 42 V operator *(V a, double b) { return V(a.x *b, a.y*b); }
 43 V operator /(V a, double b) { return V(a.x / b, a.y / b); }
 44 struct L
 45 {
 46     P s, t;
 47     double ang;
 48     L(P X = V(), P Y = V())
 49     {
 50         s = X, t = Y, ang = (Y - X).angle();
 51     }
 52 };
 53 typedef L S;
 54 double cross(V a, V b)
 55 {
 56     return a.x*b.y - a.y*b.x;
 57 }
 58 bool operator <(const L &a, const L &b)
 59 {
 60     double r = a.ang - b.ang;
 61     if (cmp(r) != 0)    return cmp(r) == -1;
 62     //极角相同，默认偏下的更大
 63     return cmp(cross(a.t - a.s, b.t - a.s)) == -1;
 64 }
 65 double dot(V a, V b)
 66 {
 67     return a.x*b.x + a.y*b.y;
 68 }
 69 bool is_parallel(L a, L b)
 70 {
 71     return cmp(cross(a.t - a.s, b.t - b.s)) == 0;
 72 }
 73 P intersection(L a, L b)
 74 {
 75     return a.s + (a.t - a.s)*(cross(b.t - b.s, a.s - b.s)) / cross(a.t - a.s, b.t - b.s);
 76 }
 77 double area(P *p, int n)
 78 {
 79     double res = 0;
 80     p[n + 1] = p[1];
 81     for (int i = 1; i <= n; i++)
 82         res += cross(p[i], p[i + 1]);
 83     return fabs(res / 2);
 84 }
 85 bool is_right(L a, P b)
 86 //判断点b是否在直线的右边（和起点连成的向量方向和直线向量方向相反）
 87 {
 88     return cmp(cross(a.t - a.s, b - a.s)) < 0;
 89 }
 90 bool SI(L *l, int n, P *s, int &m)
 91 //增量法求半平面交
 92 {
 93     static L que[MAXN];
 94     static P que2[MAXN];
 95     int head = 0, tail = 0;
 96     sort(l + 1, l + 1 + n);
 97     que[head] = l[1];
 98     for (int i = 2; i <= n; i++)
 99     {
100         if (cmp(l[i].ang - l[i - 1].ang))
101         {
102             if (head < tail && (is_parallel(que[head], que[head + 1]) || is_parallel(que[tail], que[tail - 1])))
103                 //若两个直线共线，但是极角不同，则没有半平面交
104                 return false;
105             while (head < tail&&is_right(l[i], que2[tail - 1])) tail--;
106             while (head < tail&&is_right(l[i], que2[head])) head++;
107             que[++tail] = l[i];
108             if (head < tail)
109                 que2[tail - 1] = intersection(que[tail], que[tail - 1]);
110         }
111     }
112     while (head < tail&&is_right(que[head], que2[tail - 1])) tail--;
113     while (head < tail&&is_right(que[tail], que2[head])) head++;
114     if (tail - head <= 1) return false;
115     que2[tail] = intersection(que[head], que[tail]);
116     m = 0;
117     for (int i = head; i <= tail; i++)
118         s[++m] = que2[i];
119     return true;
120 }
121 P p[MAXN];
122 L l[MAXN];
123 double solve()
124 //求取半平面交的面积
125 //SI函数计算结果只是得到了半平面交的多边形数组
126 {
127     
128     if (!SI(l, n, p, m))
129         return 0;
130     return area(p, m);
131 }
132 int main()
133 {
134     int T;
135     scanf("%d", &T);
136     while (T--)
137     {
138         scanf("%d", &m);
139         P beg, pre;
140         for (int i = 1; i <= m; i++)
141         {
142             P a, b;
143             
144             scanf("%lf%lf", &a.x, &a.y);
145             //直线方向，从起点指向终点
146             //向量表示，终点减去起点
147             if (i == 1)
148             {
149                 pre = a;
150                 beg = a;
151                 continue;
152             }
153             n++;
154             l[n] = L(pre, a);
155             pre = a;
156         }
157         n++;
158         l[n] = L(pre, beg);
159     }
160     m = 0;
161     printf("%.3lf", solve());
162     return 0;
163 }

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps = 1e-6;
const int    MAXN = 20010;
const double lim = 10000;
const double PI = acos(-1.0);
int n, m;
inline int cmp(double x)
{
    if (x > eps)return 1;
    return x < -eps ? -1 : 0;
}
struct V
{
    double x, y;
    double ang;
    double angle()
    {//求取极角
        return atan2(y, x);
    }
    V(double X = 0, double Y = 0)
    {
        //初始化
        x = X, y = Y;
        ang = atan2(y, x);
    }
    bool operator ==(const V &b)
    {
        return cmp(x - b.x) && cmp(y - b.y);
    }

};
typedef V  P;
V operator +(V a, V b) { return V(a.x + b.x, a.y + b.y); }
V operator -(V a, V b) { return V(a.x - b.x, a.y - b.y); }
V operator *(V a, double b) { return V(a.x *b, a.y*b); }
V operator /(V a, double b) { return V(a.x / b, a.y / b); }
struct L
{
    P s, t;
    double ang;
    L(P X = V(), P Y = V())
    {
        s = X, t = Y, ang = (Y - X).angle();
    }
};
typedef L S;
double cross(V a, V b)
{
    return a.x*b.y - a.y*b.x;
}
bool operator <(const L &a, const L &b)
{
    double r = a.ang - b.ang;
    if (cmp(r) != 0)    return cmp(r) == -1;
    //极角相同，默认偏下的更大
    return cmp(cross(a.t - a.s, b.t - a.s)) == -1;
}
double dot(V a, V b)
{
    return a.x*b.x + a.y*b.y;
}
bool is_parallel(L a, L b)
{
    return cmp(cross(a.t - a.s, b.t - b.s)) == 0;
}
P intersection(L a, L b)
{
    return a.s + (a.t - a.s)*(cross(b.t - b.s, a.s - b.s)) / cross(a.t - a.s, b.t - b.s);
}
double area(P *p, int n)
{
    double res = 0;
    p[n + 1] = p[1];
    for (int i = 1; i <= n; i++)
        res += cross(p[i], p[i + 1]);
    return fabs(res / 2);
}
bool is_right(L a, P b)
//判断点b是否在直线的右边（和起点连成的向量方向和直线向量方向相反）
{
    return cmp(cross(a.t - a.s, b - a.s)) < 0;
}
bool SI(L *l, int n, P *s, int &m)
//增量法求半平面交
{
    static L que[MAXN];
    static P que2[MAXN];
    int head = 0, tail = 0;
    sort(l + 1, l + 1 + n);
    que[head] = l[1];
    for (int i = 2; i <= n; i++)
    {
        if (cmp(l[i].ang - l[i - 1].ang))
        {
            if (head < tail && (is_parallel(que[head], que[head + 1]) || is_parallel(que[tail], que[tail - 1])))
                //若两个直线共线，但是极角不同，则没有半平面交
                return false;
            while (head < tail&&is_right(l[i], que2[tail - 1])) tail--;
            while (head < tail&&is_right(l[i], que2[head])) head++;
            que[++tail] = l[i];
            if (head < tail)
                que2[tail - 1] = intersection(que[tail], que[tail - 1]);
        }
    }
    while (head < tail&&is_right(que[head], que2[tail - 1])) tail--;
    while (head < tail&&is_right(que[tail], que2[head])) head++;
    if (tail - head <= 1) return false;
    que2[tail] = intersection(que[head], que[tail]);
    m = 0;
    for (int i = head; i <= tail; i++)
        s[++m] = que2[i];
    return true;
}
P p[MAXN];
L l[MAXN];
double solve()
//求取半平面交的面积
//SI函数计算结果只是得到了半平面交的多边形数组
{
    
    if (!SI(l, n, p, m))
        return 0;
    return area(p, m);
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        scanf("%d", &m);
        P beg, pre;
        for (int i = 1; i <= m; i++)
        {
            P a, b;
            
            scanf("%lf%lf", &a.x, &a.y);
            //直线方向，从起点指向终点
            //向量表示，终点减去起点
            if (i == 1)
            {
                pre = a;
                beg = a;
                continue;
            }
            n++;
            l[n] = L(pre, a);
            pre = a;
        }
        n++;
        l[n] = L(pre, beg);
    }
    m = 0;
    printf("%.3lf", solve());
    return 0;
}

View Code

【POJ - 3335】 Rotating Scoreboard

求内核，实际上还是半平面交裸题

注意：

1.当判断点是否在右边的时候，各个直线的旋转排除是逆时针的，所以直线的方向输入也应该是逆时针

2.当判断内核是否为多边形的时候，可以求面积，当面积小于0的时候，不为多边形

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps = 1e-6;
const int    MAXN = 20010;
const double lim = 10000;
const double PI = acos(-1.0);
int n, m;
inline int cmp(double x)
{
    if (x > eps)return 1;
    return x < -eps ? -1 : 0;
}
struct V
{
    double x, y;
    double ang;
    double angle()
    {//求取极角
        return atan2(y, x);
    }
    V(double X = 0, double Y = 0)
    {
        //初始化
        x = X, y = Y;
        ang = atan2(y, x);
    }
    bool operator ==(const V &b)
    {
        return cmp(x - b.x) && cmp(y - b.y);
    }

};
typedef V  P;
V operator +(V a, V b) { return V(a.x + b.x, a.y + b.y); }
V operator -(V a, V b) { return V(a.x - b.x, a.y - b.y); }
V operator *(V a, double b) { return V(a.x *b, a.y*b); }
V operator /(V a, double b) { return V(a.x / b, a.y / b); }
struct L
{
    P s, t;
    double ang;
    L(P X = V(), P Y = V())
    {
        s = X, t = Y, ang = (Y - X).angle();
    }
};
typedef L S;
double cross(V a, V b)
{
    return a.x*b.y - a.y*b.x;
}
bool operator <(const L &a, const L &b)
{
    double r = a.ang - b.ang;
    if (cmp(r) != 0)    return cmp(r) == -1;
    //极角相同，默认偏下的更大
    return cmp(cross(a.t - a.s, b.t - a.s)) == -1;
}
double dot(V a, V b)
{
    return a.x*b.x + a.y*b.y;
}
bool is_parallel(L a, L b)
{
    return cmp(cross(a.t - a.s, b.t - b.s)) == 0;
}
P intersection(L a, L b)
{
    return a.s + (a.t - a.s)*(cross(b.t - b.s, a.s - b.s)) / cross(a.t - a.s, b.t - b.s);
}
double area(P *p, int n)
{
    double res = 0;
    p[n + 1] = p[1];
    for (int i = 1; i <= n; i++)
        res += cross(p[i], p[i + 1]);
    return fabs(res / 2);
}
bool is_right(L a, P b)
//判断点b是否在直线的右边（和起点连成的向量方向和直线向量方向相反）
{
    return cmp(cross(a.t - a.s, b - a.s)) < 0;
}
bool SI(L *l, int n, P *s, int &m)
//增量法求半平面交
{
    static L que[MAXN];
    static P que2[MAXN];
    int head = 0, tail = 0;
    sort(l + 1, l + 1 + n);
    //for (int i = 1; i <= n; i++)
    //    printf("x %lf y %lf x %lf y %lf\n", l[i].s.x, l[i].s.y, l[i].t.x, l[i].t.y);
    que[head] = l[1];
    for (int i = 2; i <= n; i++)
    {
        if (cmp(l[i].ang - l[i - 1].ang))
        {
            if (head < tail && (is_parallel(que[head], que[head + 1]) || is_parallel(que[tail], que[tail - 1])))
                //若两个直线共线，但是极角不同，则没有半平面交
                return false;
            while (head < tail&&is_right(l[i], que2[tail - 1])) tail--;
            while (head < tail&&is_right(l[i], que2[head])) head++;
            que[++tail] = l[i];
            if (head < tail)
                que2[tail - 1] = intersection(que[tail], que[tail - 1]);
        }
    }
    while (head < tail&&is_right(que[head], que2[tail - 1])) tail--;
    while (head < tail&&is_right(que[tail], que2[head])) head++;
    if (tail - head <= 1) return false;
    que2[tail] = intersection(que[head], que[tail]);
    m = 0;
    for (int i = head; i <= tail; i++)
        s[++m] = que2[i];
    return true;
}
P p[MAXN];
L l[MAXN];
double solve()
//求取半平面交的面积
//SI函数计算结果只是得到了半平面交的多边形数组
{

    if (!SI(l, n, p, m))
        return -1;
    return area(p, m);
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        scanf("%d", &n);
        P tmp, pre, beg;
        for (int i = 1; i <= n; i++)
        {
            scanf("%lf%lf", &tmp.x, &tmp.y);
            if (i == 1)
            {
                pre = beg = tmp;
                continue;
            }
            l[i - 1] = L(tmp, pre);
            pre = tmp;
        }
        l[n] = L(beg, tmp);
        //for (int i = 1; i <= n; i++)
        //    printf("x %lf y %lf x %lf y %lf\n", l[i].s.x, l[i].s.y, l[i].t.x, l[i].t.y);
        if (solve() < 0)
            printf("NO\n");
        else
            printf("YES\n");
        //printf("%lf ", solve());
    }

    return 0;
}

View Code

posted @ 2019-07-27 16:31 rentu 阅读(369) 评论(0) 编辑收藏举报

刷新页面返回顶部

rentu

算法学习：半平面交

公告