算法学习:莫比乌斯反演
【前置知识】
【数论分块】
【问题描述】求令i从1到n,i整除k的和
【解决方法】显而易见的,1~n的某个区间内,i整除k的值是相同的,所以我们只需要找到这个区间,然后用区间个数乘以这个区间的贡献(即i整除k的值)

1 int res=0; 2 for(int d=1;d<=nn;) { 3 int enn = nn/(nn/d); 4 int en = min(enn,nn); 5 res += (nn/d)*(d+en)*(en+1-d)/2; 6 d = en+1; 7 }
【积性函数】
对 函数F(X) ,满足当a,b互质时,有F(a*b)=F(a)*F(b),则称函数F(X)为积性函数
积性函数一般都可以通过埃筛或者线性筛常数时间求取
此处列举几个比较重要且常用的积性函数
φ(x) : 欧拉函数,小于等于x且和x互质的数的个数
Ι (x): 函数值恒为1的函数
id(x): 函数值等于x的函数
ε(x): 元函数,只有当x等于1时为1,其余情况均为0
【莫比乌斯函数】
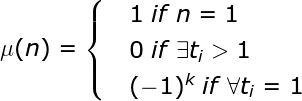
ti 是指第 i 个数的质因子的幂次方
函数定义是:
1.当n==1时,函数值等于1
2.当有质因子的幂次方大于1的情况,函数为0
3.当所有的质因子的幂次方都等于1时,函数为(-1)的k次方,k指不同的质因子的个数
求1~MAXN的莫比乌斯函数的代码板子

1 int mu[MAXN], prime[MAXN],vis[MAXN],sum[MAXN]; 2 int cnt = 0; 3 void init() 4 { 5 mu[1] = 1; 6 cnt = 0; 7 for (int i = 2; i < MAXN; i++) 8 { 9 if (vis[i] == 0) 10 { 11 mu[i] = -1; 12 prime[++cnt] = i; 13 } 14 for (int j = 1; j <= cnt && i*prime[j]<MAXN; j++) 15 { 16 vis[prime[j] * i] = 1; 17 if (i%prime[j] == 0) 18 { 19 mu[i*prime[j]] = 0; 20 break; 21 } 22 else 23 { 24 mu[i*prime[j]] = -mu[i]; 25 } 26 } 27 } 28 for (int i = 1; i < MAXN; i++) 29 sum[i] = sum[i - 1] + mu[i]; 30 }
莫比乌斯函数还有一个特殊的性质:
令F(x)等于,x的所有因子的莫比乌斯函数的和
则F(x)的函数值只有当x为1时等于1,其余情况均为0
(利用质因子互质的性质可以证出来,此处就不给出证明)
【狄利克雷卷积】

狄利克雷卷积是对两个函数进行操作,函数f,g的卷积等于,令d为n的因子,有f(d)*g(n/d),n的所有因子的和即为f,g的狄利克雷卷积
有性质:
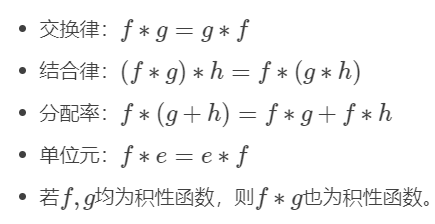
由上面的狄利克雷卷积定义我们可以得到以下结论:
【结论一】由莫比乌斯函数的特殊性质可知,有 I*μ==ε
【结论二】和莫比乌斯函数类似,欧拉函数也有一特殊性质:
令F(x)等于,x的所有因子的欧拉函数的和
则F(x)的函数值为x
(利用欧拉函数的定义可以证出来,此处就不给出证明)
1. φ*Ι==id
2. φ==id*μ
推导和结论如下:
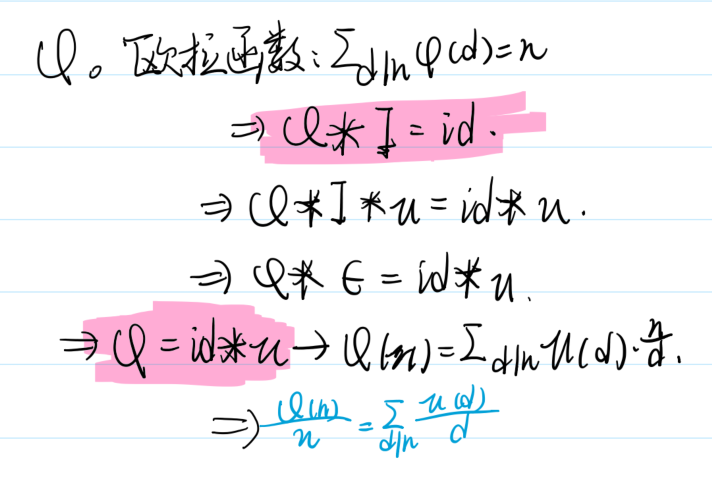
【莫比乌斯反演】

(摘自https://oi-wiki.org/math/mobius/)
推导过程如下







