图

一、学习总结

1.1图的思维导图

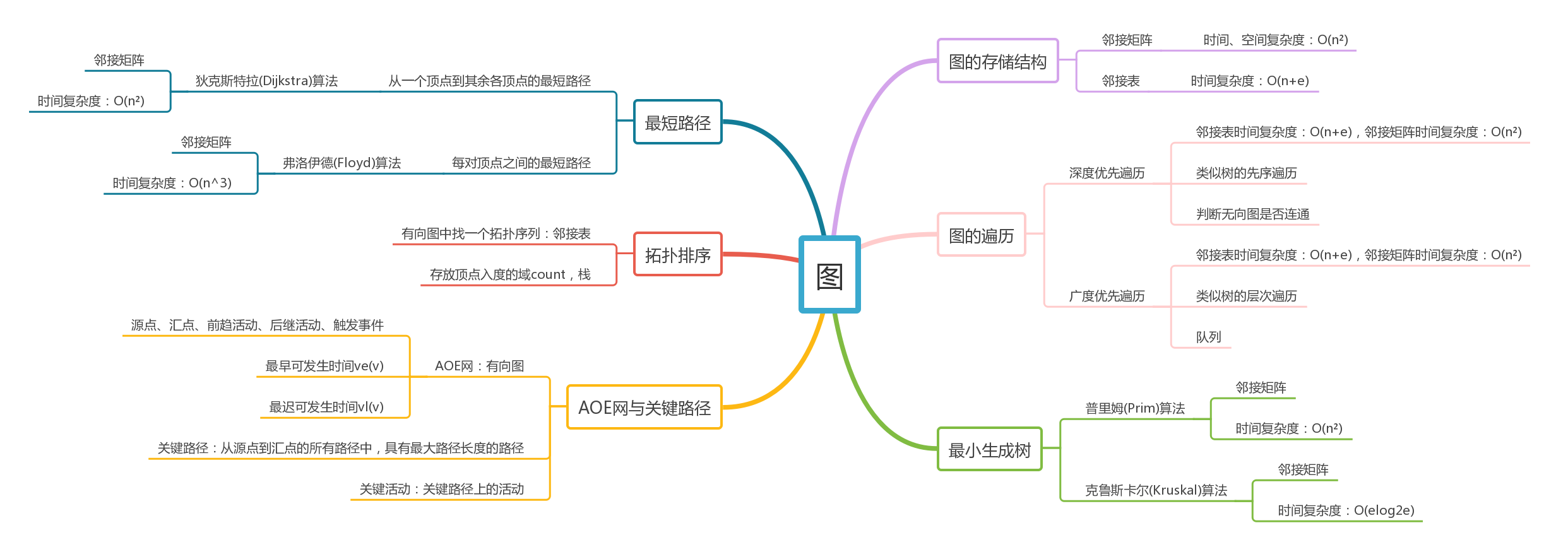
1.2图结构学习体会

（1）深度优先遍历算法：从某个初始顶点出发，访问完初始顶点后，接着访问初始顶点的未被访问过的邻点，然后再访问该邻点的未被访问过的邻点，如果该邻点的所有邻点都访问过，则访问上一级的未被访问过的其他顶点，直至所有顶点都访问结束。类似于树的先序遍历。 

（2）广度优先遍历算法：从某个初始顶点出发，访问完初始顶点后，接着访问初始顶点的所有未被访问过的邻点，然后访问初始顶点的第一个邻点的所有未被访问过的邻点，初始顶点的第二个邻点的所有未被访问过的邻点，直至所有顶点都访问结束。类似于树的层次遍历。

（3）Prim算法：从某个初始顶点出发，将该初始顶点到各顶点的最短路径放入数组lowcost[]中，取数组lowcost[]中的最小值，取该顶点加入最小生成树的顶点集中，接着修改数组lowcost[]（加入该顶点不导致产生回路），如此循环，直到生成最小生成树。

（4）Kruscal算法：用一个结构体数组E[]存放图的所有边，每次都寻找最小权值的那条边，并且满足加入该边的顶点后不会形成回路，如果形成回路则放弃这条边，继续寻找未被探访过的边，直至生成最小生成树。

（5）Dijkstra算法：从某个初始顶点出发，将该初始顶点放入数组path[]中，将该初始顶点到各顶点的最短路径放入数组dist[]中，取数组dist[]中的最小值，根据图的结构修改数组dist[]，如果数组dist[]修改了，则数组path[]相对应的位置也要进行修改。

（6）Floyd算法：初始化数组A[]为图的邻接矩阵，数组Path[]都为-1。从第一个顶点开始考虑，如果A[i][j]>A[i][k]+A[k][j]，则A[i][j]=A[i][k]+A[k][j]，Path[i][j]=k，直到最后一个顶点考虑结束。

（7）拓扑排序算法：利用栈，将入度为0的顶点进栈。在栈不为空时循环，将栈顶元素出栈，同时将该顶点的所有后继顶点的入度减1，将入度为0的相邻顶点进栈，然后找下一个相邻顶点直至结束。

二、PTA实验作业

1.1、题目1：7-1 QQ帐户的申请与登陆

1.2、设计思路（伪代码或流程图）

　　这题的思路很清晰,通过L和N判断新用户还是老用户,然后再一步步往下走。难点在于如何利用STL中的map快速解决。

1.3、代码截图

1.4、PTA提交列表说明

 

 

2.1 题目2 7-3 七度空间

2.2 伪代码

int main()  
{  
    定义 整型变量i, a, b, j，浮点型t;  
    输入n，m  
    给head初始化  
   循环输入结点关系
    从i=1到i=n循环
    {  
       vis初始化 
        t = bfs(i) * 100.0 / n;  
        输出结点及其所占百分比
    }  
    return 0;  
}

2.3 代码截图

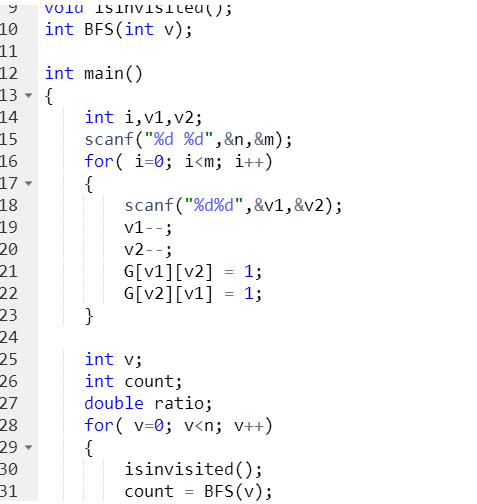
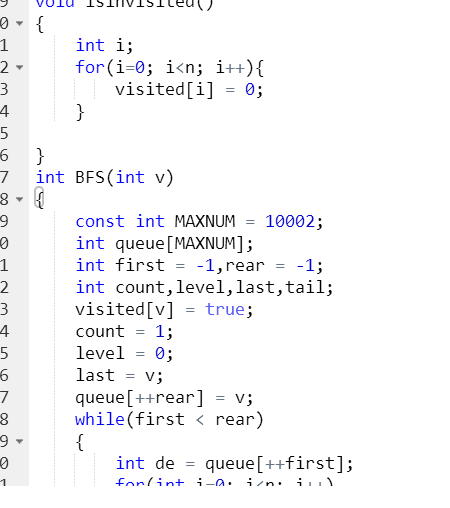
2.4、PTA提交列表说明

在求u经过的节点时,由于采用了递归函数,前两次都误将其他节点当作u经过的结点,导致出错。后来发现错误：T==NULL时应返回0而不是返回m。在操作过程中,粗心大意,忘记分析如果该节点为u时的操作

3.1 题目3 7-4 公路村交通

3.2 设计思路

先用邻接矩阵的方法存储图，然后就运用Prim算法求出这个图的最小生成树，最后输出最少费用dist

3.3 代码截图

 

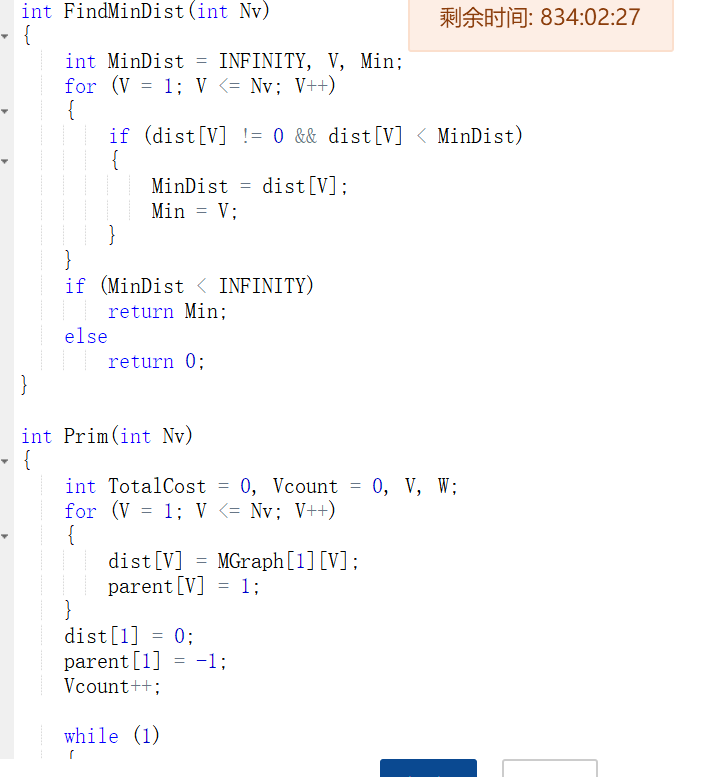
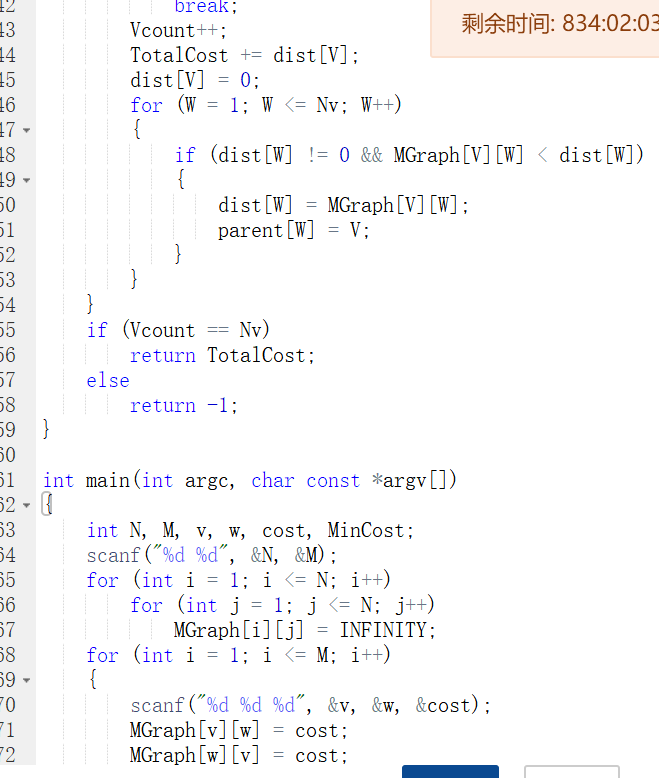
7.4 提交列表

三、PTA最后排名 

四、阅读代码

 本次PTA题集中的7-7 旅游规划：

本题是一个Dijkstra的变式应用题。关键在于题目中说的，在路径都最短时输出花费最小的那个路径。就对原有的Dijkstra算法做了两点改动。都在找到最小边加入之后更新其他边时发生，一是当找到新加点的最短路径后，将路径和花费金钱都更新。二是若找到最短路径和原有的最短路径相同。那么只更新花费为小的那个即可。因为此题并没有要求输出最小的那个路径，所以在这一步里没有必要去做父亲结点数组。但如果要求输出路径，就需要再开一个数组做回朔了。