或许是 oi 生涯最后做的几道题了

这么丧不太好啊，振作起来。

最近状态极差，省队有点困难。

学了三年多 oi，最后 noi 都没去过，想想都有些可惜啊。

不过能见识这么多有趣的人、有趣的算法题，我也知足了。

CF549E. Sasha Circle

将圆的一般方程写为 \(x^2+y^2=Dx+Ey+F\) 也就是空间中一个平面和一个椭圆抛物面相交的方程。将所有点投射到椭圆抛物面 \(z=x^2+y^2\) 上，转化为寻找一个平面分割红蓝点至两侧。

红点的上凸包一定存在一个面满足条件。将三维的上凸包投射到二维，是二维凸包的一个三角剖分。

凸包上每条边所在三角形，对应这条边极大的包含凸包的圆。可以分治去寻找这个三角剖分。

至于判定一个三角形对应圆：凸包上每条边，经过他的所有圆圆心是一条直线，每个红蓝点会限制圆心在一个区间上。（这个维护角度的 \(\tan\) 即可。）

复杂度 \(\mathcal O(C^{2/3}(n+m))\)。代码很具有技巧性。

CF674G. Choosing Ads

推广 \(\mathcal O(1)\) 空间寻找一个序列的众数的方法。

好像叫摩尔投票法。出发点是，每次删去 \(k\) 个不同的数，出现次数 \(>\frac 1k\) 的数一定会被留下。

这东西是支持合并的，可以放到线段树上做。至多有 \(5\) 个数超过 \(p\%\)，暴力维护。

CF575E. Spectator Riots

肯定能拍齐所有人，原因类似 CF549E。

每个人可能到达的区域是个菱形，端点拿出来做凸包，答案显然是凸包上的三个点。

对应三个点 \(i,j,k\) 构成的合法圆，如果 \((i,j)\) 之间有另外的点 \(l\)，令圆不经过 \(k\) 转而经过 \(l\)，半径会更大。因此答案一定是凸包上连续的三个点。

ARC102F. Revenge of BBuBBBlesort!

猜了个逆序对数是 3 的倍数，然后就想不动了。这篇题解 就是往这个方向做的，但是不知道怎么证明正确性。

还是去寻找一些规律。先倒过来转为从 \(1\dots n\) 操作到排列 \(p\)。

可以发现相邻的两个位置是不能都操作的，从任意方案最靠右的操作点开始讨论可以证明。那么意味着，\(p\) 中满足 \(p_i=i\) 的才可能成为操作点。

距离 \(\ge 2\) 的操作点互不影响，分开考虑。对于每一段内的非操作点，他在操作过程中一定只沿一个方向移动，意味着 \(p\) 中这些相同方向的点要保证有序。

线性解决。

CF809E. Surprise me!

\[\varphi(a_i\cdot a_j)=a_i\cdot a_j\cdot\frac{\frac{\varphi(a_i)}{a_i}\frac{\varphi(a_j)}{a_j}}{\frac{\varphi(\gcd(a_i,a_j))}{\gcd(a_i,a_j)}}=\frac{\gcd(a_i,a_j)}{\varphi(\gcd(a_i,a_j))}\cdot \varphi(a_i)\cdot \varphi(a_j) \]

那么枚举 \(\gcd\) 进行莫比乌斯反演，把所有倍数拿出来建虚树，转化为求 \(\sum_{i,j}\varphi(a_i)\cdot \varphi(a_j)\cdot \mathrm{dis}(i,j)\)。

\(\mathcal O(n\log^2n)\)。

LOJ#3022. 「CQOI2017」老 C 的方块

发现任何一个模板块，都是蓝线左右各有一个大小为 2 的连通块。如此四色染色：

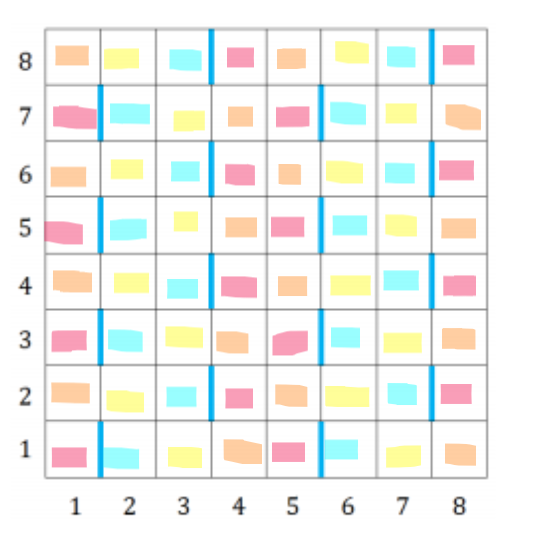
容易得到最小割建图。

CF1288F. Red-Blue Graph

令每条边向右流代表红色，向左流代表蓝色。那么每个点的限制可以描述为出入度的大小关系。

利用流守恒，新建虚点给予带有下界的流量，跑上下界最小费用可行流。

LOJ#2537. 「PKUWC2018」Minimax

\(f(u,i)\) 表示 \(u\) 节点值为 \(i\) 的概率。合并左右儿子 \(x,y\) 时，有转移

\[f(u,i)=f(x,i)\times \left(p\sum_{j<i}f(y,j)+(1-p)\sum_{j>i}f(y,j)\right)\qquad f(x,i)\neq 0 \]

\(f(y,i)\neq 0\) 同理。这样就可以用线段树合并维护。

LOJ#3340. 「NOI2020」命运

DP 状态记录子树内未覆盖点对中，起点深度最深的点。那么合并子树时讨论哪边的点作为最深点，可以发现是整体 DP 的模型。

AGC010E. Rearranging

不互质的两个数的相对顺序不会发生变化，连一条边。

Alice 需要给这张无向图定向为 DAG，Bob 则是求一个字典序最大的拓扑序。考虑定向：

连通块之间独立，分块考虑。取连通块中最小的点，这个点一定能成为第一个点（以她为根的外向生成树）。删去她之后，可以递归的去做。

一种简单的实现方式是边表排序后 dfs。

CF932F. Escape Through Leaf

转移形如 \(f_u=a_u\times b_v+f_v\)，李超线段树合并维护。

因为合并过程中，每条直线只会被下放，复杂度 \(\mathcal O(n\log n)\)。

LOJ#2473. 「九省联考 2018」秘密袭击

将第 \(k\) 大转化一下：

\[\begin{aligned} \sum_S \mathrm{kth}(S)&=\sum_{S}\sum_{i}[\mathrm{kth}(S)=i]i\\ &=\sum_{i}\sum_{S}\left[\mathrm{cnt}_{\ge i}(S)\ge k\right] \end{aligned} \]

可以设计 DP \(f(u,i,j)\) 表示 \(u\) 子树中包含 \(j\) 个 \(\ge i\) 的点的连通块个数。最外层枚举 \(i\) 可以做到 \(\mathcal O(Wn^2)\)。

\(j\) 这一位的转移是卷积，放到 GF 上。直接使用多项式乘法无法优化，注意到每个 \(u\) 的答案加起来也是一个 \(n\) 次多项式，带入 \(n+1\) 个点值 DP 后再插值即可。

同时记录 \(g(u,i)\) 为子树内 \(f(u,i)\) 之和。此时 DP 转移形如 \(f\) 整体加、\(f\) 区间乘、\(g\) 加上 \(f\)、两个 \(f\) 按位乘。

设变换 \((a,b,c,d):(f,g)\to (af+b,cf+g+d)\)。因为是关于 \(f,g\) 的线性变换，满足结合律。

由此可以线段树合并维护，\(\mathcal O(n^2\log W)\)。（实现时需要注意内存分配。）

---

哎模拟赛题不改不行，先咕会儿。