2021.12.20 模拟赛
计数场。
T1 AGC036F. Square Constraints
zzz 哥哥搬的 AGC nb 题。
首先观察,是在 \((0,0),(2n-1,2n-1)\) 的矩形中,画半径 \(n,2n\) 的圆,令两圆之间的整点为 \(1\),其余为 \(0\)。求矩形格点形成矩阵的积和式。
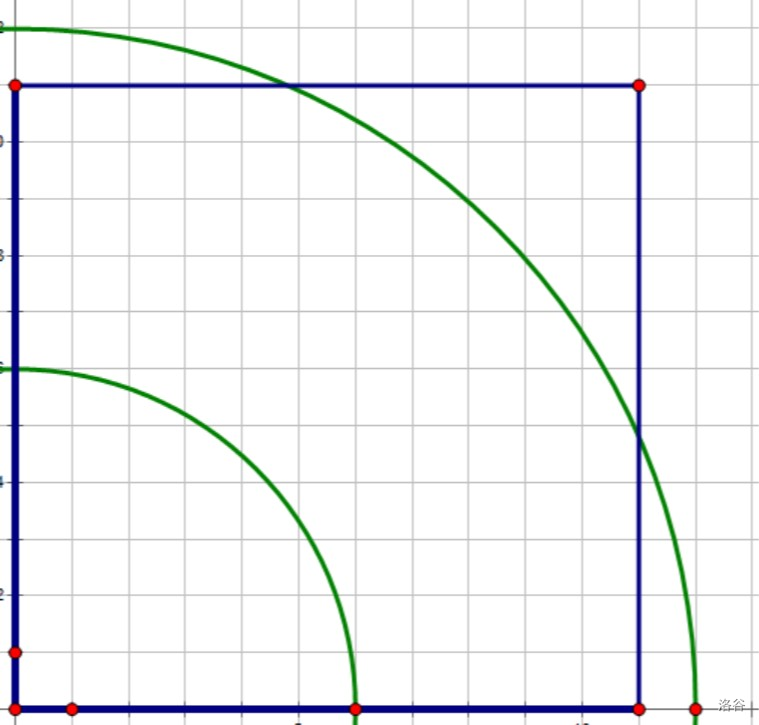
先考虑没有小圆的限制,那么从上到下,一行一行地放点,设第 \(i\) 行可放位置数为 \(R_i\),答案为 \(\prod_i(R_i-i+1)\)。
对于小圆,考虑容斥,下方有 \(n\) 行受到小圆限制,枚举其中 \(k\) 行放在小圆内进行容斥。
要计算这一部分的方案数,每放一个点需要知道其限制 \(R_i\) 或 \(r_i\) 在所有行中的排名。
上面 \(n\) 行称为 \(A\) 类,下面 \(n\) 行称为 \(B\) 类。\(A\) 类按 \(R_i\) 为关键字,\(B\) 类按 \(r_i\) 为关键字,排序。
这样:
- \(A\) 类的排名,就是它前面的 \(A\) 类个数和 \(B\) 类选择 \(r_i\) 的个数;
- \(B\) 类选择 \(r_i\) 时,排名也是它前面的 \(A\) 类个数和 \(B\) 类选择 \(r_i\) 的个数;
- \(B\) 类选择 \(R_i\) 时,排名是所有 \(A\) 类个数、\(B\) 类选择 \(r_i\) 个数、和它前面 \(B\) 类选择 \(R_i\) 的个数。
那么 DP 设 \(f_k(i,j)\) 表示前 \(i\) 行有 \(j\) 个 \(B\) 类选择 \(r_i\),的方案数。做 \(k\) 遍 DP 是必要的,因为计算 \(B\) 类选择 \(R_i\) 的排名需要确定 \(k\)。
复杂度 \(\mathcal O(n^3)\)。
T2 「LibreOJ NOI Round #2」不等关系
zrq 学长讲过的题诶。
只满足 \(\texttt <\) 关系的话,答案是个多重集排列 \(\dfrac{n!}{\prod a_i!}\)。
这样算会让一些 \(\texttt >\) 不满足,考虑容斥,枚举 \(\texttt >\) 的一个子集 \(|T|\) 强制不满足,容斥系数为 \((-1)^{|T|}\)。
关注每选一个 \(\texttt >\) 对容斥系数的贡献,那么可以做一个 DP,\(f_i\) 表示前 \(i\) 个段的 \(\frac{1}{\prod a_i!}\) 乘容斥系数之和。发现转移是半在线卷积,分治 NTT 即可 \(\mathcal O(n\log^2n)\)。
T3 ARC102E. Stop. Otherwise...
对于权值 \(i\),如果 \(i<x\),\(i\) 和 \(x-i\) 只能允许其中一个被选;特别地,\(i=x-i\) 时,这个值至多选一个;其余的值随意选。
设第一类权值对有 \(a\) 个,随意选的权值有 \(b\) 个。
列出式子,
可以 \(\mathcal O(n^3)\)。
改一改,
把 T2 写的 NTT 粘过来就 \(\mathcal O(n^2\log n)\) 了。
幸好给的 \(2000\),简单卡卡常就过了。
下面记录一个更优秀的做法:
- 考虑二选一权值对的 OGF为 \(1+2x+2x^2+\dots\);
- 至多选一次的权值的 OGF 为 \(1+x\);
- 随意选的权值的 OGF 为 \(1+x+x^2+\dots\)。
最后分配 \(n\) 个骰子的权值,答案为
我们知道 \([x^i](1+x)^A=\dbinom{A}{i}\),\([x^i]\dfrac{1}{(1-x)^B}=\dbinom{i+B-1}{B-1}\),每次可以 \(\mathcal O(n)\) 卷积得到单点答案。总复杂度 \(\mathcal O(nK)\)。


