Go语言数据结构与算法-堆
概念
堆这种数据结构的应用场景非常多,最经典的莫过于堆排序。堆排序是一种原地的、时间复杂度为 O(nlogn)
- 堆是一个完全二叉树
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值
树
什么树?

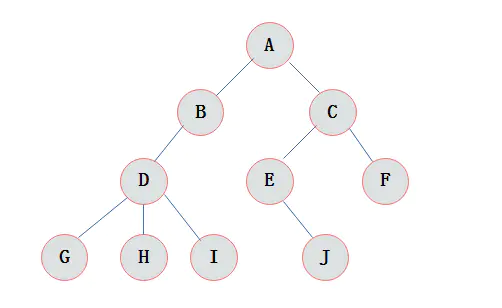
树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn,其中每一个集合本身又是一棵树,并且称为根的子树
树的定义还需要强调以下两点:
- n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
- 子树的个数没有限制,但它们一定是互不相交的。
下图是一棵普通的树
二叉树
什么是二叉树?
官方定义:在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作左子树(left subtree)和右子树(right subtree)
人话: 只有2个分叉的树, 每个节点最多有两个子树的树结构
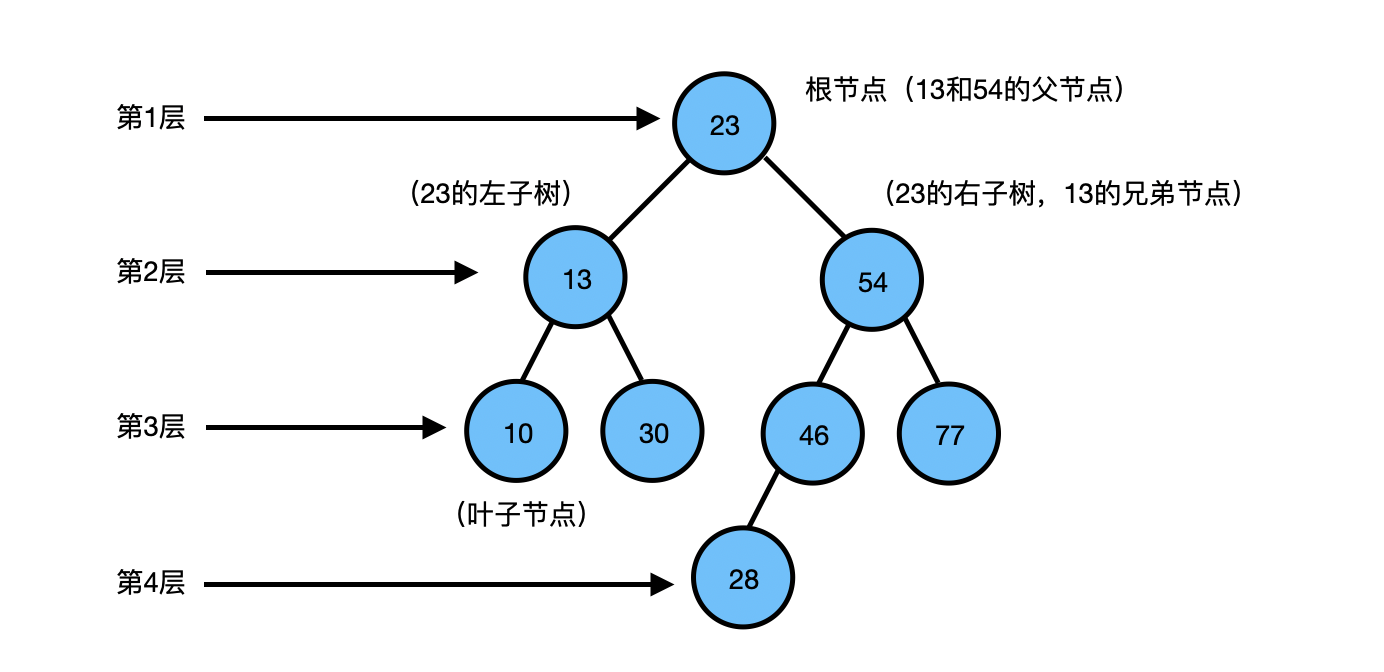
- 根节点:一棵树最上面的节点称为根节点。
- 父节点、子节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子 节点。
- 叶子节点:没有任何子节点的节点称为叶子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
- 节点度:节点拥有的子树数。上图中,13的度为2,46的度为1,28的度为0。
- 树的深度:从根节点开始(其深度为0)自顶向下逐层累加的。上图中,13的深度是1,30的深度是2,28的深度是3。
- 树的高度:从叶子节点开始(其高度为0)自底向上逐层累加的。54的高度是2,根节点23的高度是3。
对于树中相同深度的每个节点来说,它们的高度不一定相同,这取决于每个节点下面的叶子节点的深度。上图中,13和54的深度都是1,但是13的高度是1,54的高度是2
二叉树分类
- 满二叉树(Perfect Binary Tree)
- 完全二叉树(Complete Binary Tree)
满二叉树
完全二叉树的一种特殊情况, 满二叉树(Perfect Binary Tree)
满二叉树的每层都是是满的,像一个稳定的三角形: 如下
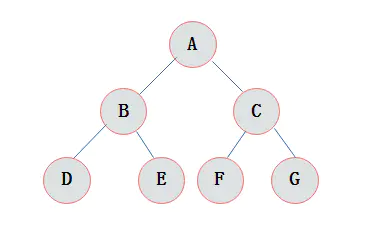
完整的定义: 除最后一层无任何子节点外,每一层上的所有节点都有两个子节点,最后一层都是叶子节点, 简单来说就是满了
满足下列性质:
1)一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
2)叶子节点数(最后一层)为2k−1;
3)第 i 层的节点数是:2i−1;
4)总节点数是:2k-1,且总节点数一定是奇数。
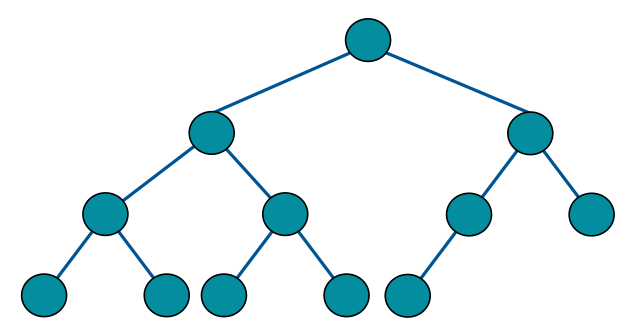
完全二叉树
每一层都是紧凑靠左排列的, 上层排满了, 才能排下层, 每层先排满左节点,才能排右节点
再论堆
- 堆是一个完全二叉树
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值
- 大顶堆: 堆中每一个节点的值都必须大于等于其子树中每个节点的值。
- 小顶堆:堆中每一个节点的值都必须小于等于其子树中每个节点的值。
下图中 那些是大顶堆,那些是小顶堆?
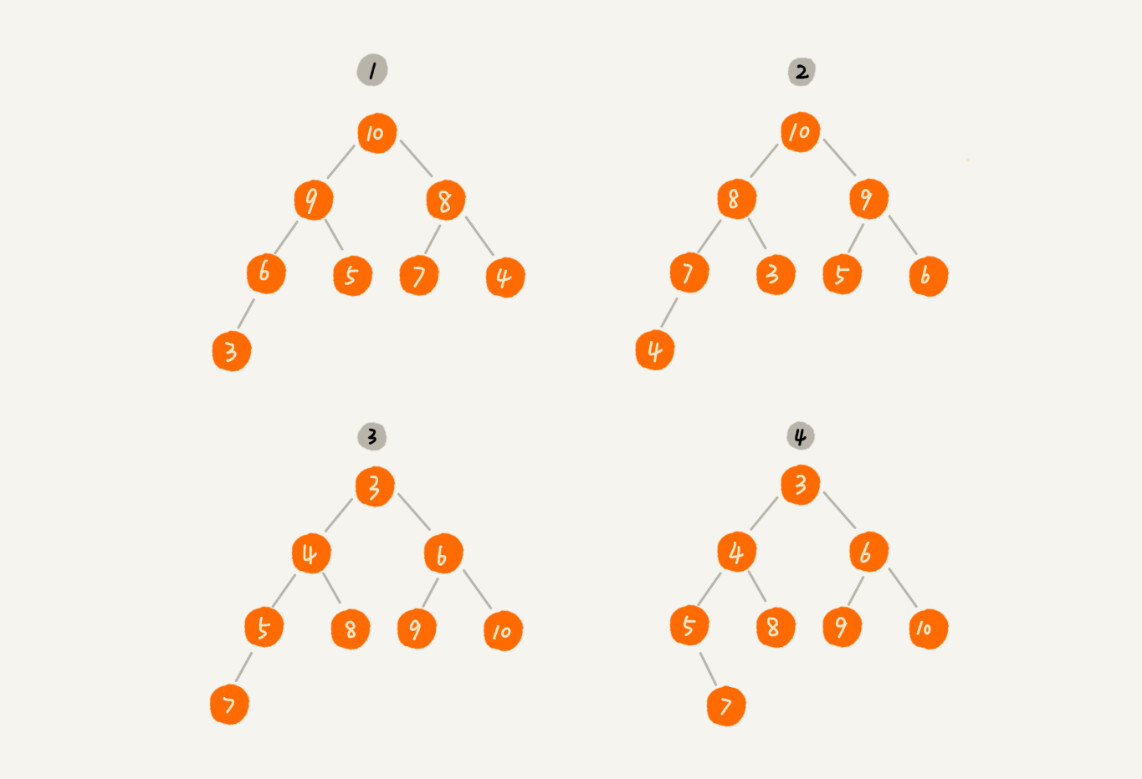
结论:
- 1,2为 大顶堆
- 3 小顶堆
- 4 不是堆
堆与数组 - 建堆
比如有如下一个大顶堆:
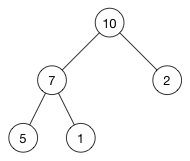
该怎么存储它? 答案是使用数组(slice)
虽然用数组来实现树相关的数据结构也许看起来有点古怪,但是它在时间和空间上都是很高效的,准备将上面的例子中的树这样存储
[10, 7, 2, 5, 1 ]
如果不允许使用指针,那么怎么知道哪一个节点是父节点,哪一个节点是它的子节点呢?
节点在数组中的位置索引index 和它的父节点以及子节点之间的索引存在一个映射关系。
堆的底层表示
如果 i 是节点的索引,那么下面的公式就给出了它的父节点和子节点在数组中索引下标的位置:
parent(i) = floor((i - 1)/2)
left(i) = 2i + 1
right(i) = 2i + 2 // right(i) # 就是简单的 left(i) + 1。左右节点总是处于相邻的位置
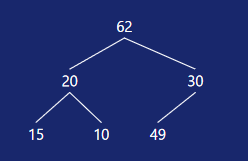
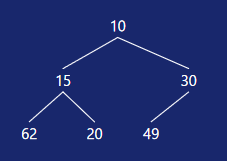
上图是一个初始状态的堆,把它调整符合条件的小根堆 最终结果如下图:
通过公式自己实现
package main
import "fmt"
// AdjustTraingle 如果只是修改slice里的元素,不需要传slice的指针;如果要往slice里append或让slice指向新的子切片,则需要传slice指针
func AdjustTraingle(arr []int, parent int) {
left := 2*parent + 1
if left >= len(arr) {
return
}
right := 2*parent + 2
minIndex := parent
minValue := arr[minIndex]
if arr[left] < minValue {
minValue = arr[left]
minIndex = left
}
if right < len(arr) {
if arr[right] < minValue {
minValue = arr[right]
minIndex = right
}
}
if minIndex != parent {
arr[minIndex], arr[parent] = arr[parent], arr[minIndex]
//递归。每当有元素调整下来时,要对以它为父节点的三角形区域进行调整
AdjustTraingle(arr, minIndex)
}
}
// ReverseAdjust
func ReverseAdjust(arr []int) {
n := len(arr)
if n <= 1 {
return
}
lastIndex := (n + 1) / 2 * 2
//逆序检查每一个三角形区域
for i := lastIndex; i > 0; i -= 2 {
parent := (i - 1) / 2
AdjustTraingle(arr, parent)
}
}
func main() {
arr := []int{62, 20, 30, 15, 10, 49}
ReverseAdjust(arr)
fmt.Println(arr)
}
>>>>>>
[10 15 30 62 20 49]
数组索引和数节点层级之间的关系:
array: 10 7 2 5 1
index: 0 1 2 3 4
level: 1 2 2 3 3
这里有一个更大的堆,它有15个节点被分成了4层:
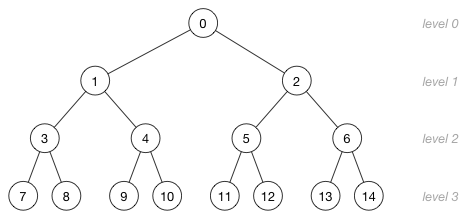
下图中的数字不是节点的值,而是存储这个节点的数组索引!这里是数组索引和树的层级之间的关系:
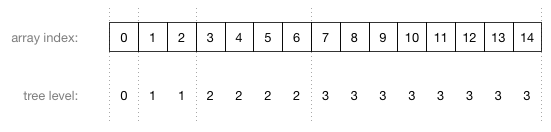
二叉数, 指定层 可以容纳的元素是固定的, 2^level, 这个是二叉数的特性决定的, 把数组按照2^n次方, 切分成多层, 每层放对应的元素, 就实现了一维 到二维的映射
如你所见,对数组进行特定方式的映射, 在不使用指针的情况下就可以找到任何一个节点的父节点或者子节点。事情比简单的去掉指针要复杂,但这就是交易:节约了空间,但是要进行更多计算【即空间换时间】。幸好这些计算很快并且只需要O(1)的时间
往堆里添加元素
通过一个插入例子来看看插入操作的细节。将数字16插入到这个堆中
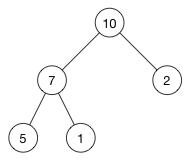
堆的数组是: [ 10, 7, 2, 5, 1 ]。 第一步是将新的元素插入到数组的尾部。数组变成: [ 10, 7, 2, 5, 1, 16 ] 相应的树变成了:
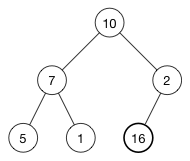
16 被添加最后一行的第一个空位。 不行的是,现在堆属性不满足,因为2在16的上面,需要将大的数字放在上面(这是一个最大堆) 为了恢复堆属性,需要交换16和2。

现在还没有完成,又因为 10 也比 16 小,继续交换插入的新元素16和它的父节点,直到它的父节点比它大或者到达树的顶部。这就是所谓的上移(shift-up),每一次插入操作后都需要进行。它将一个太大或者太小的数字浮起到树的顶部。
最后得到的堆:
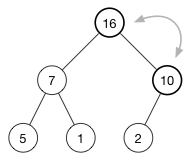
现在每一个父节点都比它的子节点大。
弹出堆顶的元素
将这个树中的 (10) 删除
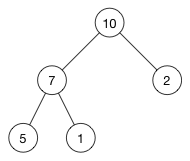
现在顶部有一个空的节点,怎么处理?
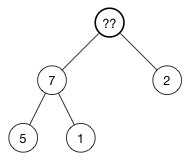
当插入节点的时候,将新的值返给数组的尾部。现在来做相反的事情:取出数组中的最后一个元素,将它放到树的顶部,然后再修复堆属性
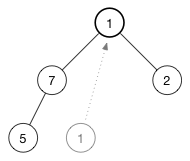
为了保持最大堆的堆属性,需要树的顶部是最大的数据。现在有两个数字可用于交换 7 和 2。选择这两者中的最大值放在树的顶部,所以交换 7 和 1,现在树变成了
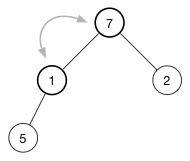
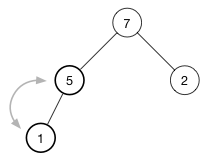
继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。对于堆,只需要再有一次交换就恢复了堆属性
实现堆
堆的核心操作:
- 堆化(Init)
- 往堆里添加元素(Push)
- 弹出堆顶的元素(Pop)
Go提供了container/heap标准库已经实现堆的操作
// The Interface type describes the requirements
// for a type using the routines in this package.
// Any type that implements it may be used as a
// min-heap with the following invariants (established after
// Init has been called or if the data is empty or sorted):
//
// !h.Less(j, i) for 0 <= i < h.Len() and 2*i+1 <= j <= 2*i+2 and j < h.Len()
//
// Note that Push and Pop in this interface are for package heap's
// implementation to call. To add and remove things from the heap,
// use heap.Push and heap.Pop.
type Interface interface {
sort.Interface
Push(x interface{}) // add x as element Len()
Pop() interface{} // remove and return element Len() - 1.
}
只要实现了这五个方法,就可以定义一个堆
注意:接口的Push和Pop方法是供heap包调用的,请使用heap.Push和heap.Pop来向一个堆添加或者删除元素。
heap包操作提供了这些方法:
// 在修改第i个元素后,调用本函数修复堆,比删除第i个元素后插入新元素更有效率。复杂度O(log(n)),其中n等于h.Len()。
func Fix(h Interface, i int)
//初始化一个堆。一个堆在使用任何堆操作之前应先初始化。Init函数对于堆的约束性是幂等的(多次执行无意义),并可能在任何时候堆的约束性被破坏时被调用。本函数复杂度为O(n),其中n等于h.Len()。
func Init(h Interface)
//删除并返回堆h中的最小元素(不影响约束性)。复杂度O(log(n)),其中n等于h.Len()。该函数等价于Remove(h, 0)。
func Pop(h Interface) interface{}
//向堆h中插入元素x,并保持堆的约束性。复杂度O(log(n)),其中n等于h.Len()。
func Push(h Interface, x interface{})
//删除堆中的第i个元素,并保持堆的约束性。复杂度O(log(n)),其中n等于h.Len()。
func Remove(h Interface, i int) interface{}
package heap_test
import (
"container/heap"
"fmt"
)
// An IntHeap is a min-heap of ints.
type IntHeap []int
func (h IntHeap) Len() int { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *IntHeap) Push(x interface{}) {
// Push and Pop use pointer receivers because they modify the slice's length,
// not just its contents.
*h = append(*h, x.(int))
}
func (h *IntHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
// This example inserts several ints into an IntHeap, checks the minimum,
// and removes them in order of priority.
func Example_intHeap() {
h := &IntHeap{2, 1, 5}
heap.Init(h)
heap.Push(h, 3)
fmt.Printf("minimum: %d\n", (*h)[0])
for h.Len() > 0 {
fmt.Printf("%d ", heap.Pop(h))
}
// Output:
// minimum: 1
// 1 2 3 5
}
如果需要大顶堆该怎么办?
// 调整比较的逻辑 这是小顶堆, 前面的元素 堆顶 要比 后面的都小
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
// 如果是大顶堆, 前面的元素 堆顶 要比 后面的都大
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
应用
- 堆排序
- 构建堆O(N)
- 不断地删除堆顶O(NlogN)
- 求集合中最大的K个元素
- 用集合的前K个元素构建小根堆
- 逐一遍历集合的其他元素,如果比堆顶小直接丢弃;否则替换掉堆顶,然后向下调整堆
- 把超时的元素从缓存中删除
- 按key的到期时间把key插入小根堆中
- 周期扫描堆顶元素,如果它的到期时间早于当前时刻,则从堆和缓存中删除,然后向下调整堆
高性能定时器
有一个定时器,定时器中维护了很多定时任务,每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间(比如 1 秒),就扫描一遍任务,看是否有任务到达设定的执行时间。如果到达了,就拿出来执行。请进行优化。
2021.7.31 11:30 TaskA
2021.8.1 1:20 TaskB
2021.8.1 1:21 TaskC
2021.8.1 23:23 TaskD
如上所述,这样每隔 1 秒就去扫描的方法比较低效:
- 每个任务的约定执行时间之间可能会隔很久,这样会多出很多无用的扫描。
- 每次都去扫描整个任务列表的话,如果该表比较大,扫描时间间隔又及其短,对性能时间消耗就比较大了。
解决方案
优先级队列
按照任务设定的执行时间,将这些任务存储在优先级队列中,队列首部(也就是小顶堆的堆顶)存储的是最先执行的任务。
这样,定时器就不需要每隔 1 秒就扫描一遍任务列表了。
它先拿队首任务的执行时间点,与当前时间点相减,得到一个时间间隔 T。
这个时间间隔 T 就是,从当前时间开始,需要等待多久,才会有第一个任务需要被执行。
这样,定时器就可以设定在 T 秒之后,再来执行任务。从当前时间点到(T-1)秒这段时间里,定时器都不需要做任何事情。
当 T 秒时间过去之后,定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值,把这个值作为定时器执行下一个任务需要等待的时间。
这样,定时器既不用间隔 1 秒就轮询一次,也不用遍历整个任务列表,性能也就提高了。完美!
package main
import (
"container/heap"
"fmt"
)
type Item struct {
value string // 优先级队列中的数据,可以是任意类型,这里使用string
priority int // 优先级队列中节点的优先级
index int // index是该节点在堆中的位置
}
// 优先级队列需要实现heap的interface
type PriorityQueue []*Item
// 绑定Len方法
func (pq PriorityQueue) Len() int {
return len(pq)
}
// 绑定Less方法,这里用的是小于号,生成的是小根堆
// 交换的标准是 优先级
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].priority < pq[j].priority
}
// 绑定swap方法
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
pq[i].index, pq[j].index = i, j
}
// 绑定push方法
func (pq *PriorityQueue) Push(x interface{}) {
item := x.(*Item)
// 标记该元素的索引位置
item.index = len(*pq)
*pq = append(*pq, item)
}
// 绑定put方法,将index置为-1是为了标识该数据已经出了优先级队列了
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
item.index = -1
return item
}
// 更新修改了优先级和值的item在优先级队列中的位置
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
item.value = value
item.priority = priority
heap.Fix(pq, item.index)
}
func main() {
// 创建节点并设计优先级
items := map[string]int{"TaskA": 5, "TaskB": 3, "TaskC": 9}
i := 0
pq := make(PriorityQueue, len(items)) // 创建优先级队列,并初始化
for k, v := range items { // 将节点放到优先级队列中
pq[i] = &Item{
value: k,
priority: v,
index: i}
i++
}
heap.Init(&pq) // 初始化堆
item := &Item{ // 创建一个item
value: "TaskD",
priority: 1,
}
heap.Push(&pq, item) // 入优先级队列
pq.update(item, item.value, 6) // 更新item的优先级
for len(pq) > 0 {
item := heap.Pop(&pq).(*Item)
fmt.Printf("priority:%d value:%s index:%d\n", item.priority, item.value, item.index)
}
}
>>>>>>output
priority:3 value:TaskB index:-1
priority:5 value:TaskA index:-1
priority:6 value:TaskD index:-1
priority:9 value:TaskC index:-1

