算法【普通二叉树】
前言:
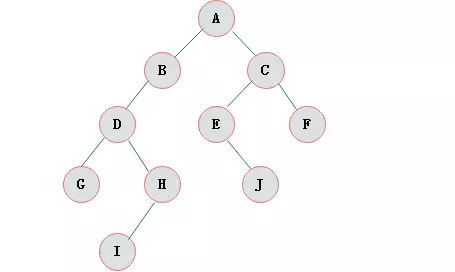
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
二叉树通常作为数据结构应用,典型用法是对节点定义一个标记函数,将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆,并应用于高效率的搜索和排序。
二叉树是一个有根树,并且每个节点最多有2个子节点。非空的二叉树,若树叶总数为 n0,分支度为2的总数为 n2,则 n0 = n2 + 1。
- 根节点
- 柱状结构最上层的一个节点
- 叶子节点
- 左叶子节点
- 右叶子节点
- 完整的子树
- 特性:二叉树中的任意一个节点都可以被视为另一颗子树的根节点
- 是由根节点,左右叶子节点组成
- 非完整的子树
- 根节点,左叶子节点
- 根节点,右叶子节点
- 根节点
广度优先遍历
参见:广度优先搜索
和深度优先遍历不同,广度优先遍历会先访问离根节点最近的节点。二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。
- 逐层遍历。横向遍历。
#封装节点
class Node():
def __init__(self,item):
self.item = item
self.left = None
self.right = None
class Tree():
def __init__(self):
# 构建一个空树
self.root = None
def addNode(self,item):
node = Node(item)
#树为空
if self.root == None:
self.root = node
return
#树为非空
cur = self.root #根节点
q_list = [cur]
while True:
first_item = q_list.pop(0)
# 判断取出节点的左节点是否为空,不为空加入到列表
if first_item.left != None:
q_list.append(first_item.left)
else:
first_item.left = node
break
#判断右叶子节点是否为空
if first_item.right != None:
q_list.append(first_item.right)
else:
first_item.right = node
break
def traverse(self):
cur = self.root
q_list = [cur]
while q_list:
first_item = q_list.pop(0)
print(first_item.item)
if first_item.left != None:
q_list.append(first_item.left)
if first_item.right != None:
q_list.append(first_item.right)
tree = Tree()
tree.addNode(1)
tree.addNode(2)
tree.addNode(3)
tree.addNode(4)
tree.addNode(5)
tree.traverse()
>>>
1
2
3
4
5
深度优先遍历
参见:深度优先搜索
在深度优先级中,我们希望从根结点访问最远的结点。和图的深度优先搜索不同的是,不需记住访问过的每一个结点,因为树中不会有环。前序,中序和后序遍历都是深度优先遍历的特例。
前(先)序、中序、后序遍历
- 深度遍历:竖向遍历。需要作用在二叉树的每一颗子树
- 前序:根左右
- 中序:左根右(想象成树结构整体顺时针走)
- 后序:左右根(想象成树结构整体逆时针走)
遍历二叉树:L、D、R分别表示遍历左子树、访问根结点和遍历右子树,则先(根)序遍历二叉树的顺序是DLR,中(根)序遍历二叉树的顺序是LDR,后(根)序遍历二叉树的顺序是LRD。还有按层遍历二叉树。这些方法的时间复杂度都是O(n),n为结点个数。
#封装节点
class Node():
def __init__(self,item):
self.item = item
self.left = None
self.right = None
class Tree():
def __init__(self):#构建一个空树
self.root = None
def addNode(self,item):
node = Node(item)
#如果树为空
if self.root == None:
self.root = node
return
#树为非空
cur = self.root
q_list = [cur]
while True:
first_item = q_list.pop(0)
#判断取出节点的左节点是否为空,不为空加入到列表
if first_item.left != None:
q_list.append(first_item.left)
else:
first_item.left = node
break
#判断右叶子节点是否为空
if first_item.right != None:
q_list.append(first_item.right)
else:
first_item.right = node
break
def forward(self,root): # 前(先)序遍历
#将根左右作用在每一颗子树中,子树和子树是基于根节点区分
#设计一个结束递归的条件
if root == None:
return
#参数root是子树的根节点
print(root.item)
self.forward(root.left)
self.forward(root.right)
def middle(self,root): #中序遍历
if root == None:
return
self.middle(root.left)
print(root.item)
self.middle(root.right)
def back(self,root): #后序遍历
if root == None:
return
self.back(root.left)
self.back(root.right)
print(root.item)
tree = Tree()
tree.addNode(1)
tree.addNode(2)
tree.addNode(3)
tree.addNode(4)
tree.addNode(5)
tree.addNode(6)
tree.forward(tree.root)
>>>
1
2
4
5
3
6
tree.middle(tree.root)
>>>
4
2
5
1
6
3
tree.back(tree.root)
>>>
4
5
2
6
3
1


