2023五一杯B题问题四----基于二分最大流最优解

4.1问题四的分析:

本题要求建立一个最小成本的运输策略,考虑最大网络流问题(Maximum Flow Problem),

对于一个带权有向图G(V,E),其中V为图中所有点的集合,E为所有边的集合,且每一条边都有它的流量上限.

这个带权有向图中有两个特殊的点:源(source)节点s和汇(sink)节点t,且这两个点满足s,t∈V,s≠t。从s到t的流函数将这个有向图的每条边e映射到一个非负实数,f(e)表示边e所承载的流量。

作为流网络，这个带权有向图需要满足两个条件：

1. 容量条件，流网络中任意边上的流量不超过流网络的容量，即对于任意边e∈E,有0<=f(e)<=Ce,其中Ce为边e能承载的流量上限
2. 守恒条件，对于非源节点和汇节点的任意内部节点e,流入该节点的流量等于流出该节点的流量,即                                                                                                                               

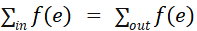
    至此,网络最大流问题就是求解源节点和汇节点之间的最大流量,对于本题来说,两个城市间的运输过程可以看作是源节点到汇节点之间的流量,在具体的运输问题,中两个城市之间的或流量是一定的,由于每条道路的承载能力有限,由给定的成本计算公式:

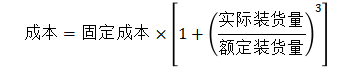
     可以观察得出当实际装货量大于额定装货量时,成本将急速攀升,对于从城市A到城市B的运输任务task(A,B),要尽量的让更多的道路来分担运输量,避免道路的实际装货量过早接近或超过其本身的额定的装货量。本题解决方法通过二分边的承载能力值使得找到一个最优的f(e)使得task(A,B)能够被完成且相应边上的实际承载量最少。

4.2最大流问题的解决办法:

    4.2.1剩余图模型

剩余图(residual graph)提供了一种搜索正向反向操作的系统方法。给定流网络 G和 G 上的流  ，定义G相对于f的剩余图如下。(参见图4-1）

1. Gf的节点集与G的节点集相同。
2. 对于f(e)<=Ce的G的每条边e = (u,v)，有Ce-f(e)个剩余容量单位，我们可以尝试正向增加流量。我们将这种方式包含的边称为正向边（forward edge）。
3. 对于f(e)>0的 G的每条边e  =(u,v),有 f(e)个容量单位，如果需要，可以通过反向增加流量来“撤销”。因此，我们在Gf中包含边e' = (u,v)  ，容量为f(e)  。注意 e'与e具有相同的端点，但其方向相反，我们将这种方式包含的边称为反向边（backward edge）。

                                                       

 

                        图4-1:图 G 有路径 s,u,v,t用于增加前 20 个流量单位;(b)结果流的余图，其中余容量紧挨着每条边虚线是新的增广路径;(c) 沿新增广路径s,v,u,t加外 10 个单位流量后的剩余图

4. 增广路:找到一条从源点到汇点的路径，使得路径上任意一条边的残量>0（注意是大于而不是大于等于，这意味着这条边还可以分配流量），这条路径便称为增广路。

4.2.2 最大流Edmonds Karp算法

最大网络流Edmonds Karp算法是对剩余图模型的具体实现,其思想为不断找到一条起点到终点的路径，若有，找出这条路径上每一条边的最小值，然后将这条路上的每一条正向边减去这条路的流量，再在这条路上的每一条反向边加上这条边的流量，再在剩下的图上寻找新的路径，使总流量增加。然后形成新的图，再寻找新路径,直到找不到从起点到终点的路径为止。对于task(A,B)来说,不妨假定每条路径上的边流过的流量相等,定义EK(A,B)为从城市A到城市B的最大流,下面给出二分(Binary Search)算法,如图4-2所示:

 

 

                                                                          

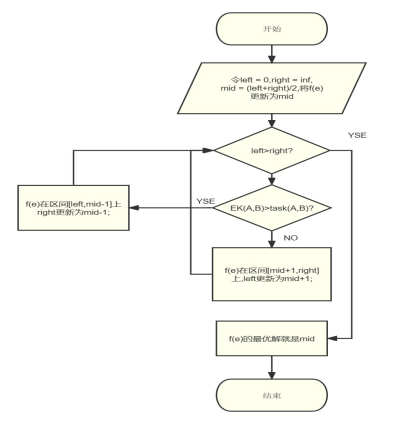
                                                                                                                            图4-2 二分法流程图

 

上述算法有一定的局限性,即单一路径上每一条边的流量均相等,为了更好的实现分流的效果,使用深度优先搜索(Depth First Search)来枚举从A到B的所有路径,通过枚举路径来确定一个解,下面给出DFS算法:

Algorithm     DFS算法

Input:A,B,path

Out:Path(A->B)

初始化:A = 起点城市,B = 终点城市,path = A                                                           

(1)    if A == B then                                                        //如果找到一条从A到B的路径

(2)        Path(A->B) += path                                                //将这条路径添加到Path(A->B)中

(3)        return                                                             //本层递归结束,退栈

(4)    else                                                                   //还没有找到A到B的路径

(5)        for each node V adjacent to A do                                //对于A的所有邻接点V来说

(6)            if V is not visited then                                     //如果V没有被访问

(7)                mark V as visited                                         //将V标记为访问

(8)                DFS(V, B, path + V)                                       //求解子问题,找到从V到B的路径

(9)                mark V as unvisited                                       //回溯,标记V为未访问

(10)            end if                                                        

(11)        end for

(12)    end if

(13)    return Path(A->B)

 

至此,得到了所有A到B得路径,由于题目中规定路径数不超过五条,要尽可能的让task(A,B)流到多的分支路径上,对于本题的城市路线图:

                                   

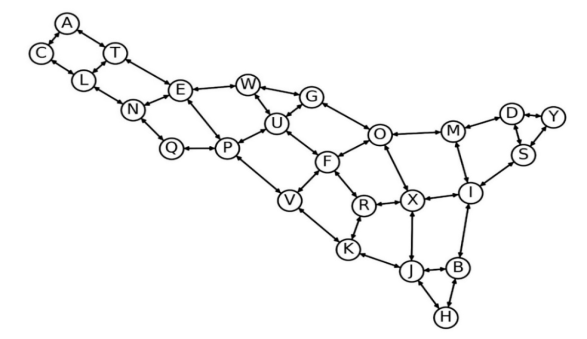
                                                                                                    图4-2  城市路径图

Path(A->B)中的部分路径为:

A->T->E->P->V->K->J->B

A->T->E->W->G->O->M->I->B

A->C->L->N->E->P->V->K->J->B

A->C->L->N->Q->P->V->K->J->B

A->C->L->T->E->P->V->K->J->B

A->T->E->N->Q->P->V->K->J->B

A->T->E->P->U->F->O->M->I->B

从A出发,首先要尽量选多分支路,即A->T和A->C同时要选,这样可以使得task(A->B)的负载在本次选择后减半。同理,在之后的选取中也要尽量选择E->P,E->W,E->N,L->T,L->N等更多的分支意味着负载会被更多道路分走,使得成本最小化。

在拿到每条边的负载后,枚举所有的边,计算当前负载下经过该边需要的成本:

                                                               

     当日运输的总成本为:

                                                                 

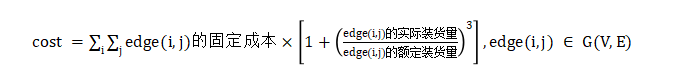
                                                                                                                                       表4 问题4结果

日期	最低运输成本
2023年4月23日	1481.74
2023年4月24日	2067.18
2023年4月25日	1687.84
2023年4月26日	1297.33
2023年4月27日	1238.36

 

4.3性能分析

时间开销:对于图G(V,E)来说,EK需要VE^2的时间开销,DFS需要E^2的时间开销,为了简化处理,在得到Path(A->B)后,我们仅选路径最短的前十条路径考虑,则处理最优路径分支需要10*当日任务数量*E的开销,综上时间复杂度为O(VE^2+tasks*E),对于本题来说,E = 78,当日任务数量<100,则5*10^5;

空间开销:存下图G(V,E)需要V+E的空间开销,在一次任务中保存路径需要V^2的空间开销,则算法的空间复杂度为O(V+E+tasks*V^2)。假设题目中数据均可使用int_32保存,则具体的内存消耗memory≈300kb