第322场周赛第3题-两个城市间路径的最小分数

给你一个正整数 n ，表示总共有 n 个城市，城市从 1 到 n 编号。给你一个二维数组 roads ，其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条 双向 道路，道路距离为 distancei 。城市构成的图不一定是连通的。

两个城市之间一条路径的 分数 定义为这条路径中道路的 最小 距离。

城市 1 和城市 n 之间的所有路径的 最小 分数。

注意：

一条路径指的是两个城市之间的道路序列。
一条路径可以 多次 包含同一条道路，你也可以沿着路径多次到达城市 1 和城市 n 。
测试数据保证城市 1 和城市n 之间 至少 有一条路径。
 

示例 1：

 

 

 

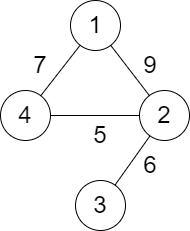
输入：n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出：5
解释：城市 1 到城市 4 的路径中，分数最小的一条为：1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。
示例 2：

 

 

 

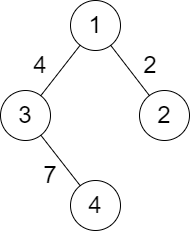
输入：n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出：2
解释：城市 1 到城市 4 分数最小的路径是：1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。
 

提示：

2 <= n <= 105
1 <= roads.length <= 105
roads[i].length == 3
1 <= ai, bi <= n
ai != bi
1 <= distancei <= 104
不会有重复的边。
城市 1 和城市 n 之间至少有一条路径。

思路:简单图论,将所有边按权值从小到大排序,因为题目保障了1到n一定有路,用dfs试点1到最小边的终点有没有一条通路,若有该边的权值就是答案.

class Solution {
int cnt = 0,head[100005] = {0};
int book[100005]= {0};
struct node//链式向前星存图
{
    int to;
    int next;
    int w;
} e[1000005];
inline void add(int x,int y,int w)
{
    e[++cnt].to=y;
    e[cnt].w=w;
    e[cnt].next=head[x];
    head[x]=cnt;
}
    int flag = 0;
    bool cmp(vector<int> a,vector<int> b)
    {
        return a[2]>b[2];
    }
    void dfs(int a,int b)//dfs标准模板,判断a到b是否有通路
    {
        if(flag)//dfs的出口设置非常重要,直接决定了算法的时间开销
        {
            return;
        }
        if(a==b)
        {
            flag = 1;
            return;
        }
        else
        {
          for(int i=head[a];i;i=e[i].next)
           {
             int v=e[i].to;
             if(!book[v])
             {
                book[v] =1;
                dfs(v,b);
                book[v] =0;
             }
           }
        }
    }
public:
    int minScore(int n, vector<vector<int>>& roads) {
        sort(roads.begin(), roads.end(), [](const vector<int>&a, const vector<int>&b){
        return a[2]<b[2];
        });//按权值排序
        for(int i=0;i<roads.size();i++)
        {
            add(roads[i][0],roads[i][1],roads[i][2]);
            add(roads[i][1],roads[i][0],roads[i][2]);
        }
        for(int i = 0;i<roads.size();i++)
        {
            flag = 0;
            dfs(1,roads[i][1]);
            if(flag)
            {
                return roads[i][2];
            }
        }
        return 0;
    }
};