lc第319场周赛第三题-逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

 

示例 1 ：

 

 

输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。
示例 2 ：

 

 

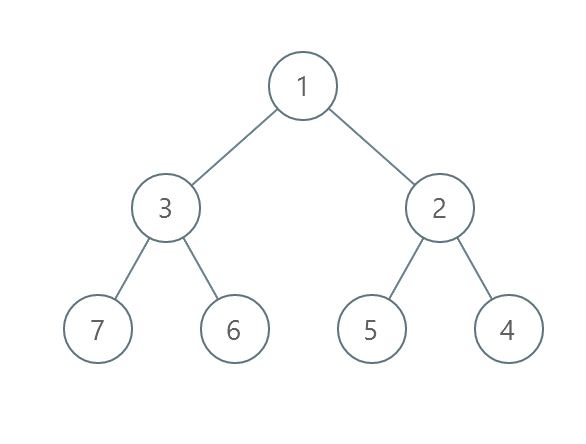
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。
示例 3 ：

 

 

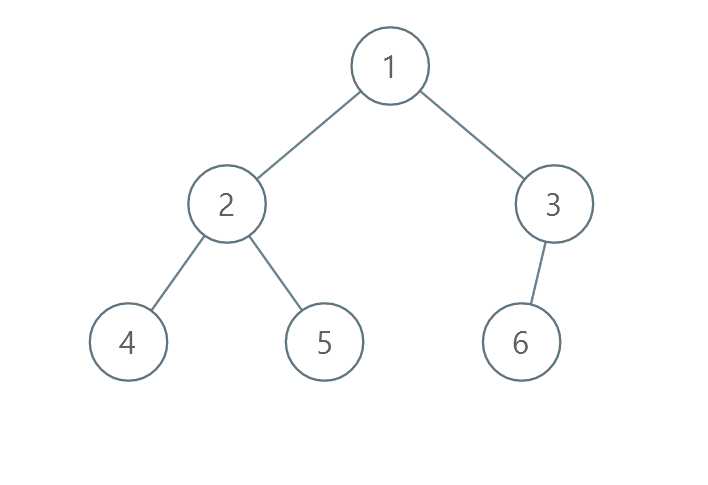
输入：root = [1,2,3,4,5,6]
输出：0
解释：每一层已经按递增顺序排序，所以返回 0 。

提示：

• 树中节点的数目在范围 [1, 105] 。
• 1 <= Node.val <= 105
• 树中的所有值 互不相同 。

分析:先用bfs层序遍历存下每一层的所有节点的值,然后对每一层的最小交换次数求和,对于一个待排序数组来说求最小交换次数使得它有序,可以利用求交换环获得

首先利用一个数组把序列里面的数的原来位置利用一个数组来记录一下，然后给原序列按照升序排序，我们知道了最终的结果，现在就是要如何从原来的位置，到达最终的位置的问题。

以样例来说明:

下标 1 2 3 4 
排序前 7 6 8 5
排序后 5 6 7 8
观察得7不在正确的位置上,所以与8交换,序列变为8 6 7 5,继续看8也不在正确的位置上,与5交换得5 6 7 8,至此7,5,8全部访问过,且三个元素构成一个交换环,6作为单点默认成环,所以一共两个交换环,要一个交换
环内所有的元素有序只需要交换该环.size()-1次,即所有环得交换次数和为数组的大小-交换环的个数次.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
vector<vector<int> > a;//存下所有层
queue<TreeNode*> q;
map<int,int> m;
int ans = 0;
void bfs(TreeNode* head)//层序遍历且能记录每层元素的标准模板
    {
        if(head!=NULL)
        q.push(head);
        while(!q.empty())
        {
          vector<int> b;
          int size = q.size();
          int k = size;
          while(size--)//保证正好取完该层
          {
          TreeNode* head1 = q.front();
          q.pop();
          b.push_back(head1->val);
          m[head1->val] = k-size-1;//这里用hash记录一下原本在层中的序数,方便求环
          if(head1->left!=NULL)
          {
              q.push(head1->left);
          }
          if(head1->right!=NULL)
          {
              q.push(head1->right);
          }
          }
          a.push_back(b);
        }
    }
public:
    int minimumOperations(TreeNode* root) {
        bfs(root);
        for(int i = 0;i<a.size();i++)
        {
            sort(a[i].begin(),a[i].end());
            int lops = 0;
            vector<int> b(a[i].size()+1,0);//用于记录是否访问过
            for(int j = 0;j<a[i].size();j++)
            {
               if(!b[j])
                   lops++;
                int k = j;
                while(!b[k])
                {
                    b[k] = 1;
                    k = m[a[i][k]];
                }
            }
            ans+=a[i].size()-lops;
        }
        return ans;
    }
};