数论::整除分块

题目链接:洛谷P3935

题目描述:

,求

 

 

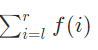
输入格式

输入共一行，两个数，l,,r。

输出格式

输出共一行，一个数，为∑f(i),i∈(l,n)对998244353取模的结果。

分析:实际上,我们有

 

 

 反演d(i),我们有d(i)等价于

不妨先设函数f(x)为该式的朴素情况

即ans等价于

 

 

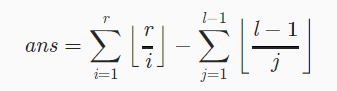
 即ans=f(r/i)-f((l-1)/j)

 对于f(x),不难看出一种O(n)的暴力算法,但是显然我们需要sqrt(n)的

我们可以先枚举观察r=10的情况,观察r/i的值

1   2  3  4  5  6  7  8  9  10
10 5  3  2  2  1  1  1  1  1

不难发现也不难证明，相同的数都是连续的，可以把它分成一块一块值相同的段。那么我们可以利用这个性质，对于每一块，将这个块的数字乘上块的长度，就可以求解这一块的和了。

首先是块的数量,在i在1到根号r之间时,最多有根号r个块,在大于根号r时,r/i<=根号r,所以一共最多有2√n种分块

当某一块的左端点为l，那么它的右端点r就是(r/(r/l))向下取整,至此,f(x)的求法为

ll ans=0;
for(ll l=1,r;l<=n;l=r+1)
{
    r=n/(n/l);
    ans+=(r-l+1)*(n/l);
}

所以Ans也可轻松解出

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long left,right;
    scanf("%lld%lld",&left,&right);
    long long sum1=0,sum2=0;
    for(long long l=1,r;l<=right;l=r+1)
    {
        r=right/(right/l);
        sum1=(sum1+(right/l)%998244353*((r-l+1)%998244353)%998244353)%998244353;
    }
    for(long long l=1,r;l<=left-1;l=r+1)
    {
        r=(left-1)/((left-1)/l);
        sum2=(sum2+((left-1)/l)%998244353*((r-l+1)%998244353)%998244353)%998244353;
    }
    printf("%lld\n",((sum1-sum2)%998244353+998244353)%998244353);
    return 0;
}