深度学习之L1、L2、smooth L1三类损失函数
一、常见的MSE、MAE损失函数
1.1 均方误差、平方损失
均方误差(MSE)是回归损失函数中最常用的误差,它是预测值与目标值之间差值的平方和,其公式如下所示: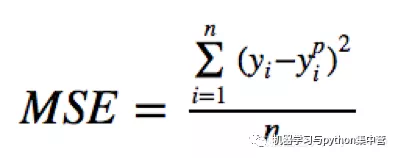
下图是均方根误差值的曲线分布,其中最小值为预测值为目标值的位置。
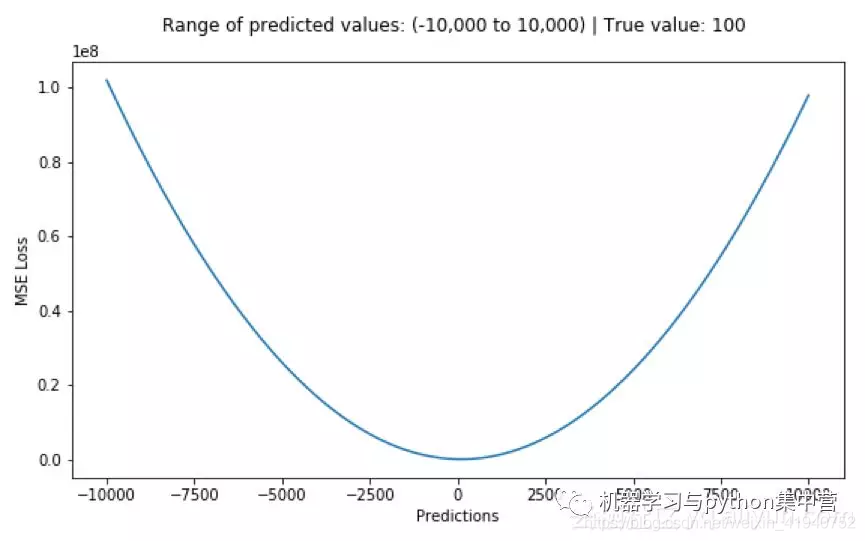
优点:各点都连续光滑,方便求导,具有较为稳定的解
缺点:不是特别的稳健,为什么?因为当函数的输入值距离中心值较远的时候,使用梯度下降法求解的时候梯度很大,可能导致梯度爆炸。
什么是梯度爆炸?误差梯度是神经网络训练过程中计算的方向和数量,用于以正确的方向和合适的量更新网络权重。
在深层网络或循环神经网络中,误差梯度可在更新中累积,变成非常大的梯度,然后导致网络权重的大幅更新,并因此使网络变得不稳定。在极端情况下,权重的值变得非常大,以至于溢出,导致 NaN 值。
网络层之间的梯度(值大于 1.0)重复相乘导致的指数级增长会产生梯度爆炸。
梯度爆炸引发的问题
在深度多层感知机网络中,梯度爆炸会引起网络不稳定,最好的结果是无法从训练数据中学习,而最坏的结果是出现无法再更新的 NaN 权重值。
1.2 平均绝对误差
平均绝对误差(MAE)是另一种常用的回归损失函数,它是目标值与预测值之差绝对值的和,表示了预测值的平均误差幅度,而不需要考虑误差的方向,范围是0到∞,其公式如下所示:
在这里插入图片描述
在这里插入图片描述
优点:无论对于什么样的输入值,都有着稳定的梯度,不会导致梯度爆炸问题,具有较为稳健性的解。
缺点:在中心点是折点,不能求导,不方便求解。
上面的两种损失函数也被称之为L2损失和L1损失。
二、L1_Loss和L2_Loss
2.1 L1_Loss和L2_Loss的公式
L1范数损失函数,也被称为最小绝对值偏差(LAD),最小绝对值误差(LAE)。总的说来,它是把目标值(Yi)与估计值(f(xi))的绝对差值的总和(S)最小化:
在这里插入图片描述
L2范数损失函数,也被称为最小平方误差(LSE)。总的来说,它是把目标值(Yi)与估计值(f(xi))的差值的平方和(S)最小化:
在这里插入图片描述
1 import numpy as np 2 3 def L1(yhat, y): 4 loss = np.sum(np.abs(y - yhat)) 5 return loss 6 7 def L2(yhat, y): 8 loss =np.sum(np.power((y - yhat), 2)) 9 return loss 10 #调用 11 yhat = np.array([0.1, 0.2, 0.3, 0.4, 0.5]) 12 y = np.array([1, 1, 0, 1, 1]) 13 14 print("L1 = " ,(L1(yhat,y))) 15 print("L2 = " ,(L2(yhat,y)))
L1范数与L2范数作为损失函数的区别能快速地总结如下:
在这里插入图片描述
2.2 几个关键的概念
(1)鲁棒性
最小绝对值偏差之所以是鲁棒的,是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值,那么最小绝对值偏差是更好的选择。
从直观上说,因为L2范数将误差平方化(如果误差大于1,则误差会放大很多),模型的误差会比L1范数来得大,因此模型会对这个样本更加敏感,这就需要调整模型来最小化误差。如果这个样本是一个异常值,模型就需要调整以适应单个的异常值,这会牺牲许多其它正常的样本,因为这些正常样本的误差比这单个的异常值的误差小。
(2)稳定性
最小绝对值偏差方法的不稳定性意味着,对于数据集的一个小的水平方向的波动,回归线也许会跳跃很大(如,在转折点处求导)。在一些数据结构上,该方法有许多连续解;但是,对数据集的一个微小移动,就会跳过某个数据结构在一定区域内的许多连续解。在跳过这个区域内的解后,最小绝对值偏差线可能会比之前的线有更大的倾斜。
相反地,最小平方法的解是稳定的,因为对于一个数据点的任何微小波动,回归线总是只会发生轻微移动;也就说,回归参数是数据集的连续函数。
三、smooth L1损失函数
其实顾名思义,smooth L1说的是光滑之后的L1,前面说过了L1损失的缺点就是有折点,不光滑,导致不稳定,那如何让其变得光滑呢?smooth L1损失函数为:
在这里插入图片描述
smooth L1损失函数曲线如下图所示,作者这样设置的目的是想让loss对于离群点更加鲁棒,相比于L2损失函数,其对离群点(指的是距离中心较远的点)、异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞。
在这里插入图片描述


 浙公网安备 33010602011771号
浙公网安备 33010602011771号