BZOJ2822:[AHOI2012]树屋阶梯(卡特兰数,高精度)
Description
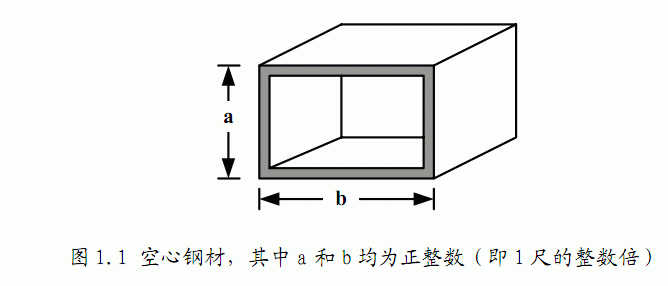
暑假期间,小龙报名了一个模拟野外生存作战训练班来锻炼体魄,训练的第一个晚上,教官就给他们出了个难题。由于地上露营湿气重,必须选择在高处的树屋露营。小龙分配的树屋建立在一颗高度为N+1尺(N为正整数)的大树上,正当他发愁怎么爬上去的时候,发现旁边堆满了一些空心四方钢材(如图1.1),经过观察和测量,这些钢材截面的宽和高大小不一,但都是1尺的整数倍,教官命令队员们每人选取N个空心钢材来搭建一个总高度为N尺的阶梯来进入树屋,该阶梯每一步台阶的高度为1尺,宽度也为1尺。如果这些钢材有各种尺寸,且每种尺寸数量充足,那么小龙可以有多少种搭建方法?(注:为了避免夜里踏空,钢材空心的一面绝对不可以向上。)
 、以树屋高度为4尺、阶梯高度N=3尺为例,小龙一共有如图1.2所示的5种搭建方法:
、以树屋高度为4尺、阶梯高度N=3尺为例,小龙一共有如图1.2所示的5种搭建方法: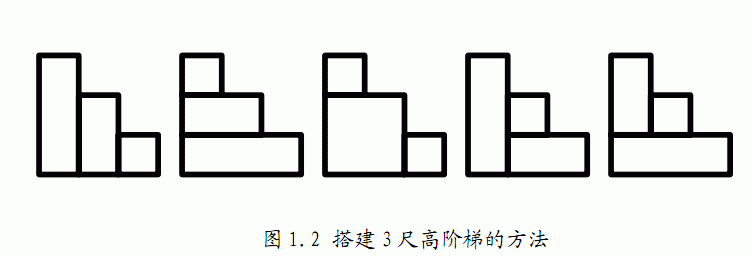
Input
一个正整数 N(1≤N≤500),表示阶梯的高度
Output
一个正整数,表示搭建方法的个数。(注:搭建方法个数可能很大。)
Sample Input
3
Sample Output
5
HINT
1 ≤N≤500
Solution
大胆猜了一波卡特兰数然后就过了
Code
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 6 int n,a[5009],cnt[1009]; 7 8 void Divide(int x,int opt) 9 { 10 for (int i=2; i<=sqrt(x); ++i) 11 while (x%i==0) x/=i,cnt[i]+=opt; 12 if (x>1) cnt[x]+=opt; 13 } 14 15 void Mul(int *a,int b) 16 { 17 int g=0; 18 for (int i=1; i<=a[0]; ++i) 19 a[i]=a[i]*b+g,g=a[i]/10,a[i]%=10; 20 while (g) a[0]++,a[a[0]]=g%10,g/=10; 21 } 22 23 int main() 24 { 25 scanf("%d",&n); 26 for (int i=n+1; i<=2*n; ++i) Divide(i,1); 27 for (int i=2; i<=n+1; ++i) Divide(i,-1); 28 a[0]=a[1]=1; 29 for (int i=2; i<=1000; ++i) 30 while (cnt[i]>=1) 31 Mul(a,i),cnt[i]--; 32 for (int i=a[0]; i>=1; --i) 33 printf("%d",a[i]); 34 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号