BZOJ2194:快速傅立叶之二(FFT)

Description

请计算C[k]=sigma(a[i]*b[i-k]) 其中 k < = i < n ，并且有 n < = 10 ^ 5。 a,b中的元素均为小于等于100的非负整数。

Input

第一行一个整数N,接下来N行，第i+2..i+N-1行，每行两个数，依次表示a[i],b[i] (0 < = i < N)。

Output

输出N行，每行一个整数，第i行输出C[i-1]。

Sample Input

5
3 1
2 4
1 1
2 4
1 4

Sample Output

24
12
10
6
1

Solution

QvQ我FFT也就能打个板子了

对FFT的运用还是不够到位，理解也只是仅仅停留在表面的地方

很多细节处以及证明并没有非常理解

啥时候数学底子够了再回来重新补FFT的证明什么奇奇怪怪的东西吧

反正学长告诉我我会打板子会用就好了

 

首先做这个题之前我还不知道FFT式子的基本形式（逃

 

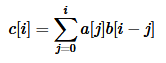
像这样下标和一定的式子就能用FFT进行优化了

下方公式转自https://blog.csdn.net/ycdfhhc/article/details/50636751

因为我不会markdown

一开始我们发现初始式子并不是FFT的形式没法搞

然后我们就将B数组翻转过来，然后发现下标和一定了……

然后把式子用另一个D表示出来，然后就可以FFT了……

答案C(0~n-1)对应D(n-1,n+n-2)

快二轮了感觉没啥希望

Code

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define N (400000+100)
using namespace std;

double pi=acos(-1.0);
int n,fn,l,r[N];
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0)
    {
        x=xx; y=yy;
    }
}a[N],b[N];

complex operator + (complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator - (complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator * (complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
complex operator / (complex a,double b){return complex(a.x/b,a.y/b);}

void FFT(int n,complex *a,int opt)
{
    for (int i=0; i<n; ++i)
        if (i<r[i])
            swap(a[i],a[r[i]]);
    for (int k=1; k<n; k<<=1)
    {
        complex wn=complex(cos(pi/k),opt*sin(pi/k));
        for (int i=0; i<n; i+=(k<<1))
        {
            complex w=complex(1,0);
            for (int j=0; j<k; ++j,w=w*wn)
            {
                complex x=a[i+j], y=w*a[i+j+k];
                a[i+j]=x+y; a[i+j+k]=x-y;
            }
        }
    }
    if (opt==-1) for (int i=0; i<n; ++i) a[i]=a[i]/n;
}

int main()
{
    scanf("%d",&n); n--;
    for (int i=0; i<=n; ++i)
        scanf("%lf%lf",&a[i].x,&b[n-i].x);
    fn=1;
    while (fn<=n+n) fn<<=1, l++;
    for (int i=0; i<fn; ++i)
        r[i]=(r[i>>1]>>1) | ((i&1)<<(l-1));
    FFT(fn,a,1); FFT(fn,b,1);
    for (int i=0; i<=fn; ++i)
        a[i]=a[i]*b[i];
    FFT(fn,a,-1);
    for (int i=n; i<=n+n; ++i)
        printf("%d\n",(int)(a[i].x+0.5));
}