BZOJ2815:[ZJOI2012]灾难(拓扑排序,LCA)
Description
阿米巴是小强的好朋友。
阿米巴和小强在草原上捉蚂蚱。小强突然想,如果蚂蚱被他们捉灭绝了,那么吃蚂蚱的小鸟就会饿死,而捕食小鸟的猛禽也会跟着灭绝,从而引发一系列的生态灾难。
学过生物的阿米巴告诉小强,草原是一个极其稳定的生态系统。如果蚂蚱灭绝了,小鸟照样可以吃别的虫子,所以一个物种的灭绝并不一定会引发重大的灾难。
我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系:
一个食物网有N个点,代表N种生物,如果生物x可以吃生物y,那么从y向x连一个有向边。
这个图没有环。
图中有一些点没有连出边,这些点代表的生物都是生产者,可以通过光合作用来生存; 而有连出边的点代表的都是消费者,它们必须通过吃其他生物来生存。
如果某个消费者的所有食物都灭绝了,它会跟着灭绝。
我们定义一个生物在食物网中的“灾难值”为,如果它突然灭绝,那么会跟着一起灭绝的生物的种数。
举个例子:在一个草场上,生物之间的关系是:
如 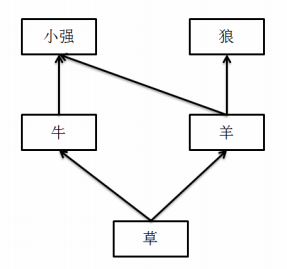
如果小强和阿米巴把草原上所有的羊都给吓死了,那么狼会因为没有食物而灭绝,而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以,羊的灾难值是1。但是,如果草突然灭绝,那么整个草原上的5种生物都无法幸免,所以,草的灾难值是4。
给定一个食物网,你要求出每个生物的灾难值。
Input
输入文件 catas.in 的第一行是一个正整数 N,表示生物的种数。生物从 1 标
号到 N。
接下来 N 行,每行描述了一个生物可以吃的其他生物的列表,格式为用空
格隔开的若干个数字,每个数字表示一种生物的标号,最后一个数字是 0 表示列
表的结束。
Output
输出文件catas.out包含N行,每行一个整数,表示每个生物的灾难值。
Sample Input
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8
Sample Output
3 6
Solution
感谢zhhe0101学长orz的耐心讲解
我太菜了听了好久才懂
不过这个题的做法的确是十分精妙的
大体分三步:1、拓扑排序2、建树3、求树的前缀和
1、我们知道,一个生物死亡的条件是他的所有食物全部死亡
而且既然这个题说了没有环,那么就可以保证食物链等级鲜明
那么求这种图,我们很容易就可以想到拓扑排序了
2、我们建一棵树,让father[x]为x的父亲,意味着若father[x]死了,那么x则灭绝
问题来了,x应该挂在哪个点上?
当然是他所有食物的LCA上啊!
若LCA死了,x的食物也会都死亡,那么x也必然死亡
建树这里可以将出度为0的点连在一个虚拟点n+1上方便处理
3、最后DFS求一下树的前缀和
因为若x死了,那么他的子树会全部死亡,那么他的重要度就是子树大小-1(去除本身)
最后附样例转树的图(学长给我画的)
5 →2 →1
↗ ↗
4 →3
6
↓
1
↙↓↘
2 3 4
↙
5
Code
1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #define MAXN (65534+5) 5 using namespace std; 6 int head1[MAXN],head[MAXN],num1,num2; 7 int n,ind[MAXN],sum,topo[MAXN]; 8 int father[MAXN],f[MAXN][17],depth[MAXN]; 9 int SUM[MAXN]; 10 11 //1为拓扑序所用邻接表 12 //2为树所用邻接表 13 struct node1 14 { 15 int to,next; 16 }edge1[MAXN*4];//这里不是很懂为什么要开MAXN*4……? 17 void add1(int u,int v) 18 { 19 edge1[++num1].to=v; 20 edge1[num1].next=head1[u]; 21 head1[u]=num1; 22 } 23 struct node 24 { 25 int to,next; 26 }edge[MAXN*2+10]; 27 void add(int u,int v) 28 { 29 edge[++num2].to=v; 30 edge[num2].next=head[u]; 31 head[u]=num2; 32 } 33 34 //toposort拓扑排序 35 //RMQ倍增做LCA的预处理 36 //LCA找两个点的最近公共祖先 37 //build将拓扑排序转换为一颗有根树 38 //DPtree求树上前缀和 39 void toposort() 40 { 41 queue<int>q; 42 for (int i=1;i<=n;++i) 43 if(ind[i]==0) 44 q.push(i); 45 46 while (!q.empty()) 47 { 48 int x=q.front(); 49 q.pop(); 50 topo[++sum]=x; 51 for (int i=head1[x];i!=0;i=edge1[i].next) 52 { 53 ind[edge1[i].to]--; 54 if(!ind[edge1[i].to]) 55 q.push(edge1[i].to); 56 } 57 } 58 } 59 void RMQ(int x) 60 { 61 f[x][0]=father[x]; 62 for (int i=1;i<=16;++i) 63 f[x][i]=f[f[x][i-1]][i-1]; 64 } 65 int LCA(int x,int y)//x is under y 66 { 67 if (depth[x]<depth[y]) swap(x,y); 68 for (int i=16;i>=0;--i) 69 if (f[x][i]!=0&&depth[f[x][i]]>=depth[y]) 70 x=f[x][i]; 71 if (x==y) return y; 72 for (int i=16;i>=0;--i) 73 if (f[x][i]!=0&&f[y][i]!=0&&f[x][i]!=f[y][i]) 74 { 75 x=f[x][i]; 76 y=f[y][i]; 77 } 78 return father[x]; 79 } 80 void build() 81 { 82 depth[n+1]=1; 83 father[n+1]=n+1; 84 for (int i=n;i>=1;--i) 85 { 86 int x=topo[i]; 87 if (head1[x]==0) 88 { 89 father[x]=n+1; 90 add(n+1,x); 91 f[x][0]=n+1; 92 depth[x]=2; 93 continue; 94 } 95 int lca=edge1[head1[x]].to; 96 for (int i=edge1[head1[x]].next;i!=0;i=edge1[i].next) 97 { 98 lca=LCA(lca,edge1[i].to); 99 } 100 father[x]=lca; 101 add(father[x],x); 102 depth[x]=depth[father[x]]+1; 103 RMQ(x); 104 } 105 } 106 void DPtree(int x) 107 { 108 SUM[x]=1; 109 for (int i=head[x];i!=0;i=edge[i].next) 110 { 111 DPtree(edge[i].to); 112 SUM[x]+=SUM[edge[i].to]; 113 } 114 } 115 116 //main函数 117 int main() 118 { 119 int x; 120 scanf("%d",&n); 121 for (int i=1;i<=n;++i) 122 { 123 scanf("%d",&x); 124 while (x!=0) 125 { 126 add1(i,x); 127 ++ind[x];//食物入度+1 128 scanf("%d",&x); 129 } 130 } 131 toposort();//拓扑排序 132 build();//建树 133 DPtree(n+1); 134 for (int i=1;i<=n;++i) 135 printf("%d\n",SUM[i]-1); 136 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号