BZOJ2521:[SHOI2010]最小生成树(最小割)

Description

Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个n个点、m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外，他还知道，某一个图可能有多种不同的最小生成树。例如，下面图 3中所示的都是图 2中的无向图的最小生成树：

 

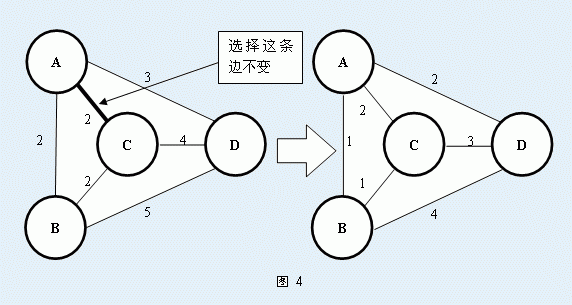
当然啦，这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB，至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中，你可以对这个无向图进行操作，一次单独的操作是指：先选择一条图中的边 P1P2，再把图中除了这条边以外的边，每一条的权值都减少1。如图 4所示就是一次这样的操作：

Input

输入文件的第一行有3个正整数n、m、Lab分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。
接下来m行依次描述标号为1,2,3…m的无向边，每行描述一条边。每个描述包含3个整数x、y、d，表示这条边连接着标号为x、y的点，且这条边的权值为d。
输入文件保证1<=x,y<=N,x不等于y,且输入数据保证这个无向图一定是一个连通图。

Output

输出文件只有一行，这行只有一个整数，即，使得标号为Lab边一定出现最小生成树中的最少操作次数。

Sample Input

4 6 1
1 2 2
1 3 2
1 4 3
2 3 2
2 4 4
3 4 5

Sample Output

1

HINT

第1个样例就是问题描述中的例子。

1<=n<=500,1<=M<=800,1<=D<10^6

Solution

首先题目的操作其实可以看成给一条边权值加一……

首先对于权值比$lab$大的边，我们肯定是不需要管的，因为按照$kruskal$的过程，他们一定在$lab$的后面考虑。

而对于权值比$lab$小的，我们可以通过给他们不停加一使得权值超过$lab$从而靠后考虑。

可以发现，当$(u[lab],v[lab])$这条边会被算到最小生成树里面，只有在权值小于等于它的边加完后，$u[lab]$和$v[lab]$不在一个连通块内。我们把权值小于等于$l[lab]$的图建出来，现在问题变成，你可以用$l[lab]-l[i]+1$的代价砍掉一些边使得$u[lab]$和$v[lab]$不连通，最小割就好了。

Code

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<queue>
 5 #include<algorithm>
 6 #define N (1009)
 7 #define INF (0x7f7f7f7f)
 8 using namespace std;
 9 
10 struct Edge{int to,next,flow;}edge[N<<1];
11 int n,m,lab,u[N],v[N],l[N],Depth[N];
12 int head[N],num_edge;
13 queue<int>q;
14 
15 inline int read()
16 {
17     int x=0,w=1; char c=getchar();
18     while (c<'0' || c>'9') {if (c=='-') w=-1; c=getchar();}
19     while (c>='0' && c<='9') x=x*10+c-'0', c=getchar();
20     return x*w;
21 }
22 
23 void add(int u,int v,int l)
24 {
25     edge[++num_edge].to=v;
26     edge[num_edge].next=head[u];
27     edge[num_edge].flow=l;
28     head[u]=num_edge;
29 }
30 
31 int DFS(int x,int low,int t)
32 {
33     if (x==t || !low) return low;
34     int f=0;
35     for (int i=head[x]; i; i=edge[i].next)
36         if (Depth[edge[i].to]==Depth[x]+1)
37         {
38             int Min=DFS(edge[i].to,min(low,edge[i].flow),t);
39             edge[i].flow-=Min;
40             edge[((i-1)^1)+1].flow+=Min;
41             f+=Min; low-=Min;
42             if (!low) break;
43         }
44     if (!f) Depth[x]=-1;
45     return f;
46 }
47 
48 bool BFS(int s,int t)
49 {
50     memset(Depth,0,sizeof(Depth));
51     Depth[s]=1;
52     q.push(s);
53     while (!q.empty())
54     {
55         int x=q.front(); q.pop();
56         for (int i=head[x]; i; i=edge[i].next)
57             if (!Depth[edge[i].to] && edge[i].flow)
58             {
59                 Depth[edge[i].to]=Depth[x]+1;
60                 q.push(edge[i].to);
61             }
62     }
63     return Depth[t];
64 }
65 
66 int Dinic(int s,int t)
67 {
68     int ans=0;
69     while (BFS(s,t)) ans+=DFS(s,INF,t);
70     return ans;
71 }
72 
73 int main()
74 {
75     n=read(); m=read(); lab=read();
76     for (int i=1; i<=m; ++i) u[i]=read(),v[i]=read(),l[i]=read();
77     for (int i=1; i<=m; ++i)
78         if (i!=lab && l[i]<=l[lab])
79         {
80             add(u[i],v[i],l[lab]-l[i]+1);
81             add(v[i],u[i],l[lab]-l[i]+1);
82         }
83     printf("%d\n",Dinic(u[lab],v[lab]));
84 }
posted @ 2019-03-13 15:02  Refun  阅读(244)  评论(0)  编辑  收藏  举报