平面应力问题7

平面应力问题

平面应力问题的平面应力应变关系

$$\begin{Bmatrix}\sigma_{xx}\\\\\sigma_{yy}\\\\\tau_{xy}\end{Bmatrix}=\frac{E}{1-\gamma^2}\begin{bmatrix}1&\gamma&0\\\\\gamma&1&0\\\\0&0&\frac{(1-\gamma)}{2}\end{bmatrix}\begin{Bmatrix}\varepsilon_{xx}\\\\\varepsilon_{yy}\\\\\gamma_{xz}\end{Bmatrix}$$

平面应变问题的应力-应变关系

$$\begin{Bmatrix}\sigma_{xx}\\\\\sigma_{yy}\\\\\tau_{xy}\end{Bmatrix}=\frac{E}{(1+v)(1-2v)}\begin{bmatrix}1-v&-v&0\\\\-v&1-v&0\\\\0&0&\frac{(1-2v)}{2}\end{bmatrix}\begin{Bmatrix}\epsilon_{xx}\\\\\epsilon_{yy}\\\\\gamma_{xy}\end{Bmatrix}$$

小变形下的应力-位移关系

$$\begin{aligned}&\varepsilon_{xx}=\frac{\partial u}{\partial x}\\&\varepsilon_{yy}=\frac{\partial\nu}{\partial y}\\&\gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial\nu}{\partial x}\end{aligned}$$

写成矩阵形式

$$\begin{Bmatrix}\varepsilon_{xx}\\\\\varepsilon_{yy}\\\\\gamma_{xy}\end{Bmatrix}=\begin{bmatrix}\frac{\partial}{\partial x}&0\\\\0&\frac{\partial}{\partial y}\\\\\frac{\partial}{\partial y}&\frac{\partial}{\partial x}\end{bmatrix}\begin{Bmatrix}u\\\\\nu\end{Bmatrix}$$

简写

$$\{\epsilon\}=[L]U$$

对于n节点的单元，未知位移的节点近似插值函数为

$$u=N_{1}u_{1}+N_{2}u_{2}+\cdots+N_{n}u_{n}\\\nu=N_{1}\nu_{1}+N_{2}\nu_{2}+\cdots+N_{n}\nu_{n}$$

矩阵形式

$$\begin{Bmatrix}u\\v\end{Bmatrix}=\begin{bmatrix}N_1&0&|&N_2&0&|&\ldots&|&N_n&0\\0&N_1&|&0&N_2&|&\ldots&|&0&N_n\end{bmatrix}\begin{Bmatrix}u_1\\\nu_1\\\nu_2\\u_2\\\nu_2\\\vdots\\u_n\\\nu_n\end{Bmatrix}$$

简写

$$\{U\}=[N]\{a\}$$

用上式中U代替 $\{\epsilon\}=[L]U$中的U

$$\{\epsilon\}=[L]U\\ \qquad=[L][N]\{a\}\\ \qquad=[B]\{a\}\\ $$

其中

$$[B]=\begin{bmatrix}\frac{\partial N_1}{\partial x}&0&|&\frac{\partial N_2}{\partial x}&0&|&\ldots&|&\frac{\partial N_n}{\partial x}&0\\\\0&\frac{\partial N_1}{\partial y}&|&0&\frac{\partial N_2}{\partial y}&|&\ldots&|&0&\frac{\partial N_n}{\partial y}\\\\\frac{\partial N_1}{\partial y}&\frac{\partial N_1}{\partial x}&|&\frac{\partial N_2}{\partial y}&\frac{\partial N_2}{\partial x}&|&\ldots&|&\frac{\partial N_n}{\partial y}&\frac{\partial N_n}{\partial x}\end{bmatrix}$$

矩阵[B] 被称为应变矩阵，可以通过插值函数$N_i(x,y)$求导得到

为了得到单元单元上的载荷与节点位移之间的关系，我们用虚功原理

$$\int\limits_{V_{e}}\delta\{\epsilon\}^{\mathrm{T}}\{\sigma\} \mathrm{d}V=\int\limits_{V_{e}}\delta\{U\}^{\mathrm{T}}\{b\} \mathrm{d}V+\int\limits_{\Gamma_{e}}\delta\{U\}^{\mathrm{T}}\{t\} \mathrm{d}\Gamma+\sum\limits_{i}\delta\{U\}_{(\{x\}=\{\overline{x}\})}^{\mathrm{T}}\{P\}_{i}$$

式中：

$\{\epsilon\}$为应变矢量；$\{\sigma\}$为应力矢量；$\{U\}$为位移矢量

$\{b\}$为体力矢量；$\{t\}$为表面力矢量

$\{P\}_i$为作用在 $\{x\}=\{\overline{x}\}$ 处的集中力矢量

d$V$为单元体积；d$\Gamma$ 为表面力$\{t\}$所作用单元的单元边界

应变的变分 δ{ε}和位移的变分 δ{U} 可以分别表示为

$$\delta\{\epsilon\}=\delta([B]\{a\})=[B]\delta\{a\}\\ \delta\{U\}=\delta([N]\{a\})=[N]\delta\{a\}$$

应力应变关系

$$\{\sigma\}=[D]\{\epsilon\}=[D][B]\{a\}$$

代入虚功原理方程

$$\int\limits_{V_{e}}\delta\{a\}^{\mathrm{T}}[B]^{\mathrm{T}}[D][B]\{a\} \mathrm{d}V=\int\limits_{V_{e}}\delta\{a\}^{\mathrm{T}}[N]^{\mathrm{T}}\{b\} \mathrm{d}V+\int\limits_{\Gamma_{e}}\delta\{a\}^{\mathrm{T}}[N]^{\mathrm{T}}\{t\} \mathrm{d}\Gamma+\sum\limits_{i}\delta\{a\}^{\mathrm{T}}[N_{((x)=(\bar{x}))}]^{\mathrm{T}}\{P\}_{i} \\ 原方程\\ \int\limits_{V_{e}}\delta\{\epsilon\}^{\mathrm{T}}\{\sigma\} \mathrm{d}V=\int\limits_{V_{e}}\delta\{U\}^{\mathrm{T}}\{b\} \mathrm{d}V+\int\limits_{\Gamma_{e}}\delta\{U\}^{\mathrm{T}}\{t\} \mathrm{d}\Gamma+\sum\limits_{i}\delta\{U\}_{(\{x\}=\{\overline{x}\})}^{\mathrm{T}}\{P\}_{i}$$

注意，对于平面单元，单元体积 d$V$和单元边界 dГ 可以分别写成 d$\nu=t$d$A$和 d$\Gamma=t$d$l$ ,式中$t$
为单元的厚度，d$A$为单元的无限小面积，d$l$为单元的无限小边界长度。
由于$\delta\{a\}$ 是节点位移的变分，因此关于坐标独立，可以把它从积分符号中拿出来并消除，方程就变为

$$\left[\int\limits_{\mathcal{A}_{c}}[B]^{\mathrm{T}}[D][B]t\mathrm{d}A\right]\{a\}=\int\limits_{\mathcal{A}_{c}}[N]^{\mathrm{T}}\{b\}t\mathrm{d}A+\int\limits_{\mathcal{L}_{c}}[N]^{\mathrm{T}}\{t\}t\mathrm{d}l+\sum\limits_{i}[N_{(\{x\}=\{\overline{x}\})}]^{\mathrm{T}}\{P\}_{i}$$

写成矩阵形式

$$[K_{e}]\{a\}=f_{e} \\ $$

$$[K_e]=\left[\int\limits_{A_e}[B]^\mathrm{T}[D][B]t\mathrm{d}A\right]$$

上式为刚度矩阵，其中

$$\{f_{e}\}=\int_{A_{e}}[N]^{\mathrm{T}}\{b\}t\mathrm{d}A+\int_{L_{e}}[N]^{\mathrm{T}}\{t\}t\mathrm{d}l+\sum_{i}[N_{((x)=\{\overline{x}\})}]^{\mathrm{T}}\{P\}_{i}$$

上式为单位力矢量

空间离散

常应变三角形(CST)单元

单元的插值函数

$$\begin{aligned} N_{1}(x,y)& =m_{11}+m_{12}x+m_{13}y \\ N_{2}(x,y)& =m_{21}+m_{22}x+m_{23}y \\ N_{3}(x,y)& =m_{31}+m_{32}x+m_{33}y \end{aligned}$$

其中

$$\begin{gathered} m_{11} =\frac{x_{2}y_{3}-x_{3}y_{2}}{2A} m_{12} =\frac{y_{2}-y_{3}}{2A} m_{13} =\frac{x_{3}-x_{2}}{2A} \\ m_{21} =\frac{x_3y_1-x_1y_3}{2A} \text{m22} =\frac{y_3-y_1}{2A} \text{m23} =\frac{x_1-x_3}{2A} \\ m_{31} =\frac{x_{1}y_{2}-x_{2}y_{1}}{2A} m_{32} =\frac{y_{1}-y_{2}}{2A} m_{33} =\frac{x_2-x_1}{2A} \end{gathered}$$

$$A=\frac{1}{2}\text{det}\begin{bmatrix}1&x_1&y_1\\1&x_2&y_2\\1&x_3&y_3\end{bmatrix}$$

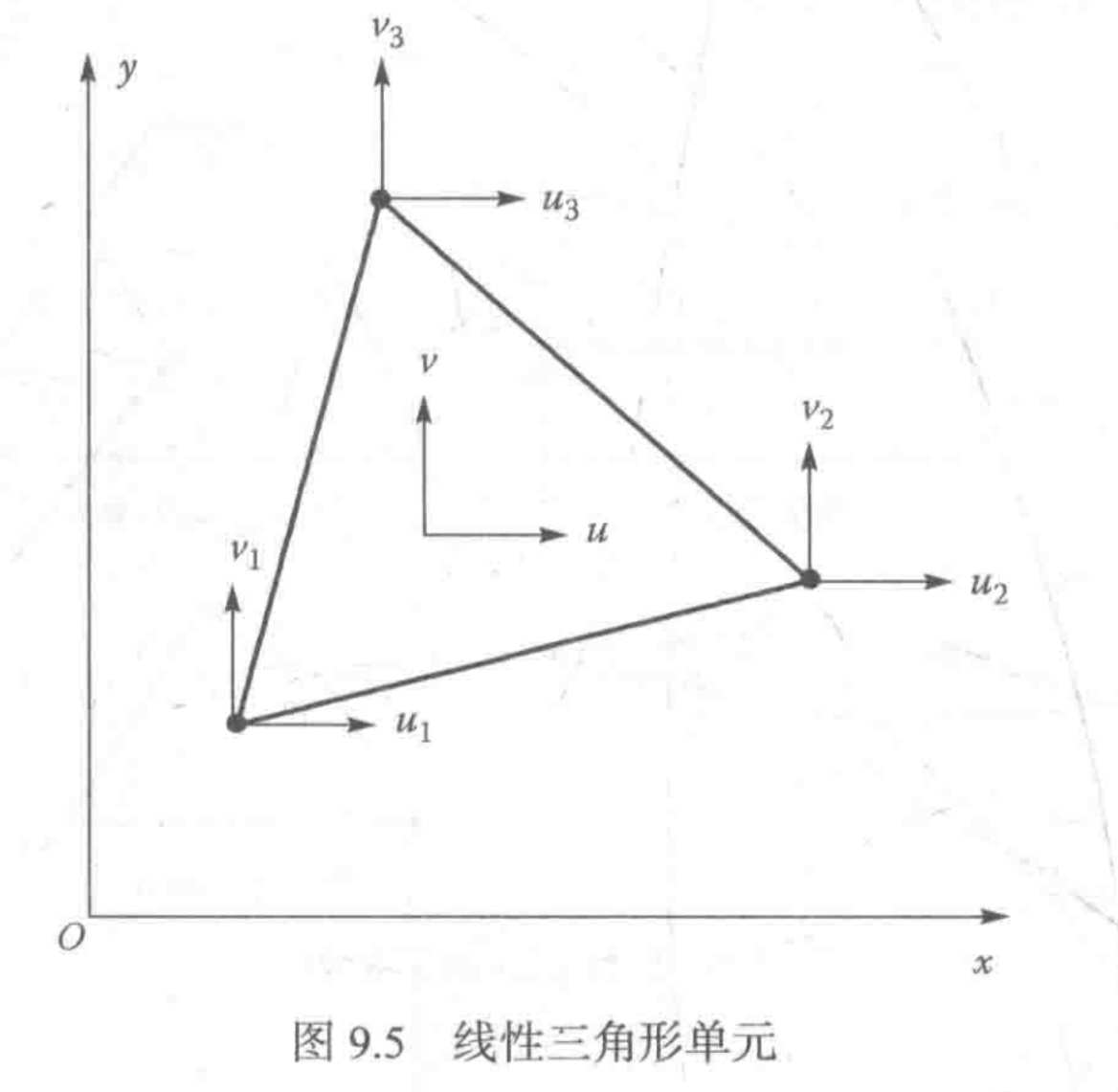
位移场

三角形单元的位移场可以表示为

$$u=N_{1}u_{1}+N_{2}u_{2}+N_{3}u_{3}\\\nu=N_{1}\nu_{1}+N_{2}\nu_{2}+N_{3}\nu_{3}$$

矩阵表示

$$\begin{Bmatrix}u\\\nu\end{Bmatrix}=\begin{bmatrix}N_1&0&|&N_2&0&|&N_3&0\\0&N_1&|&0&N_2&|&0&N_3\end{bmatrix}\begin{Bmatrix}u_1\\\nu_1\\u_2\\\nu_2\\u_3\\\nu_3\end{Bmatrix}$$

简写为

$$\{U\}=[N]\{a\}$$

应变矩阵

$$\{\epsilon\}=[B]\{a\}$$

其中

$$\begin{gathered}[B]=\begin{bmatrix}\frac{\partial N_1}{\partial x}&0&|&\frac{\partial N_2}{\partial x}&0&|&\frac{\partial N_3}{\partial x}&0\\0&\frac{\partial N_1}{\partial y}&|&0&\frac{\partial N_2}{\partial y}&|&0&\frac{\partial N_3}{\partial y}\\\frac{\partial N_1}{\partial y}&\frac{\partial N_1}{\partial x}&|&\frac{\partial N_2}{\partial y}&\frac{\partial N_2}{\partial x}&|&\frac{\partial N_3}{\partial y}&\frac{\partial N_3}{\partial x}\end{bmatrix}\end{gathered}$$

代入得

$$[B]=\begin{bmatrix}m_{12}&0&|&m_{22}&0&|&m_{32}&0\\0&m_{13}&|&0&m_{23}&|&0&m_{33}\\m_{13}&m_{12}&|&m_{23}&m_{22}&|&m_{33}&m_{32}\end{bmatrix}$$

备注：矩阵[B]与笛卡儿坐标系的$x$和 y 坐标无关，它只是节点坐标的函数，并且在整个单元内为常量，因此在整个单元内应变矢量也是常量。这就是为什么这种单元被称为“常应变三角形单元”的原因，本书中将常应变三角形单元简称为 CST(Constant Strain Triangle)单元。

由于矩阵[B]和[D]都是常数矩阵,因此刚度矩阵可表示为

$$[K_e]=[B]^\mathrm{T}[D][B]tA_e$$

其中 $A_e$为单元的面积

单位力矢量

体力

考虑体力{b}是重力引起的，因此

$$\int\limits_{A_{\epsilon}}[N]^{\mathrm{T}}\{b\}t \mathrm{d}A=t\int\limits_{A_{\epsilon}}\begin{bmatrix}N_{1}&0\\0&N_{1}\\N_{2}&0\\0&N_{2}\\N_{3}&0\\0&N_{3}\end{bmatrix}\begin{Bmatrix}0\\0\\-\rho g\end{Bmatrix}\mathrm{d}A=t\begin{bmatrix}0\\-\int\limits_{A_{\epsilon}}N_{1}\rho g \mathrm{d}A\\0\\-\int\limits_{A_{\epsilon}}N_{2}\rho g \mathrm{d}A\\0\\-\int\limits_{A_{\epsilon}}N_{3}\rho g \mathrm{d}A\end{bmatrix}$$

这里采用式(8.18)和式(8.19)给出的三角形积分公式，计算在整个单元上的插值函数的积分。运用这些公式，可将积分结果整理如下：

$$\int_{A_{e}}N_{1}\rho g \mathrm{d}A=\rho g\int_{A_{e}}N_{1}^{1}N_{2}^{0}N_{3}^{0} \mathrm{d}A=\rho g\frac{1!0!0!}{(1+0+0+2)!}2A_{e}=\rho g\frac{A_{e}}{3}\\\int_{A_{e}}N_{2}\rho g \mathrm{d}A=\rho g\int_{A_{e}}N_{1}^{0}N_{2}^{1}N_{3}^{0} \mathrm{d}A=\rho g\frac{0!1!0!}{(0+1+0+2)!}2A_{e}=\rho g\frac{A_{e}}{3}\\\int_{A_{e}}N_{3}\rho g \mathrm{d}A=\rho g\int_{A_{e}}N_{1}^{0}N_{2}^{0}N_{3}^{1} \mathrm{d}A=\rho g\frac{0!0!1!}{(0+0+1+2)!}2A_{e}=\rho g\frac{A_{e}}{3}$$

代入得

$$\int_{A_e}[N]^\mathrm{T}\{b\}t \mathrm{d}A=-\frac t3\begin{Bmatrix}0\\\rho gA_e\\0\\\rho gA_e\\0\\\rho gA_e\end{Bmatrix}$$

可以发现，单元自重在各节点是平均分配的。

表面力

如图 所示的单元作用有大小为$q$的均布载荷，该均布载荷作用在单元的边 2-3 上，并
且与 $x$ 轴的夹角为$\theta$ 。因此，表面力矢量可以表示为$\{t\}=\{-q\cos\theta,-q\sin\theta\}^\mathrm{T}\circ$

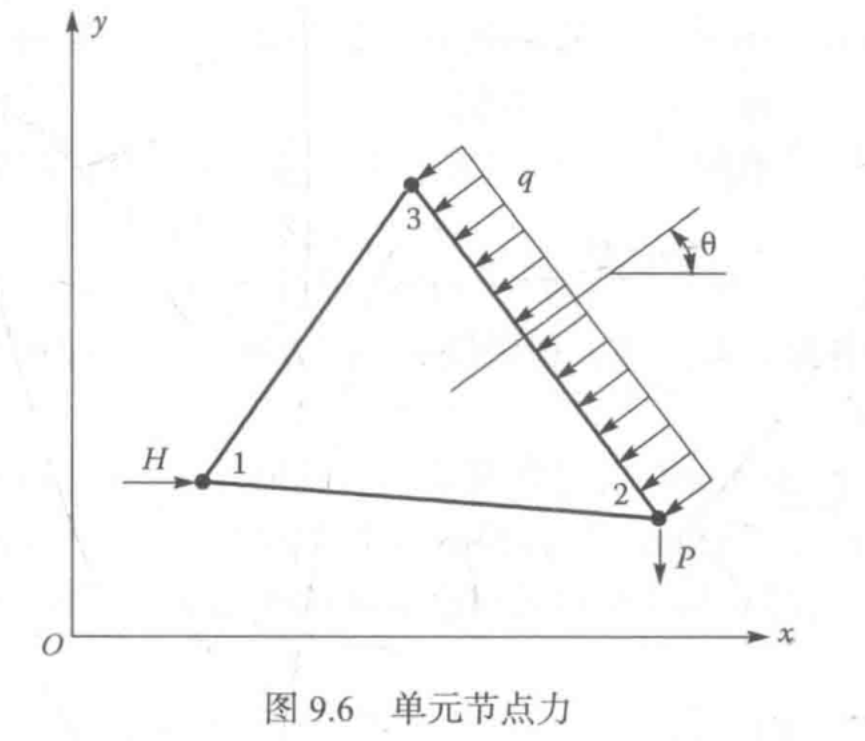
则表面力可以表示为

$$\int\limits_{L_{n}}[N]^{\mathrm{T}}\{t\}t \mathrm{d}l=\int\limits_{L_{23}}\begin{bmatrix}0&0\\0&0\\N_2&0\\0&N_2\\N_3&0\\0&N_3\end{bmatrix}\begin{Bmatrix}-q\cos\theta\\-q\sin\theta\\-q\sin\theta\end{Bmatrix}t \mathrm{d}l=t\int\limits_{L_{23}}\begin{Bmatrix}0\\0\\-N_2q\cos\theta\\\\-N_2q\sin\theta\\\\-N_3q\cos\theta\\\\-N_3q\sin\theta\end{Bmatrix}\mathrm{d}l$$

注意,在边 2-3 上 $N_1=0$

采用式(8.18)给出的沿三角形边长的积分公式来计算沿长度方向的积分。运用这个公式上式可以表示为

$$\int\limits_{L_{e}}[N]^{\mathrm{T}}\{t\}t \mathrm{d}l=t\begin{Bmatrix}0\\0\\-q\cos\theta L_{2-3}/2\\-q\sin\theta L_{2-3}/2\\-q\cos\theta L_{2-3}/2\\-q\sin\theta L_{2-3}/2\end{Bmatrix}$$

从上式可以看出,节点2和节点3平均分配了作用在它们之间的均布载荷$qL_{2-3}$。

集中力

% 文件：CST_COARSE_MESH_DATA.m
%
% 下列变量被声明为全局变量，以便被构成程序的所有函数（M文件）使用
%
global nnd nel nne nodof eldof n     % 全局变量声明
global geom connec dee nf Nodal_loads  % 包括节点数、元素数、节点每元素数、每节点自由度数等

format short e  % 设置MATLAB的输出格式为科学计数法

% 定义模型参数
nnd = 21;              % 节点数
nel = 24;              % 元素数
nne = 3;               % 每个元素的节点数
nodof = 2;             % 每个节点的自由度数
eldof = nne * nodof;   % 每个元素的自由度数

% 节点坐标x和y
geom = zeros(nnd, 3);  % 初始化几何矩阵
% ... 此处省略了具体的节点坐标赋值 ...

% 元素连接信息
connec = zeros(nel, 3);  % 初始化连接矩阵
# ... 此处省略了具体的元素连接信息 ...

% 材料属性
E = 200000.;  % 弹性模量，单位MPa
vu = 0.3;      % 泊松比
thick = 5.;    % 梁厚度，单位mm

% 形成平面应力的弹性矩阵
dee = formdsig(E, vu);  % 调用formdsig函数，该函数未在代码中给出

% 边界条件
nf = ones(nnd, nodof);  % 初始化自由度矩阵
% ... 此处省略了具体的边界条件赋值 ...

% 计算自由度的总数
n = 0;
for i = 1:nnd
    for j = 1:nodof
        if nf(i, j) ~= 0
            n = n + 1;
            nf(i, j) = n;
        end
    end
end

% 载荷
Nodal_loads = zeros(nnd, 2);  % 初始化节点载荷矩阵
% ... 此处省略了具体的载荷赋值 ...

%%%%%%%%%%%%   输入结束   %%%%%%%%%%%%%