张量(tensor)
这一术语最初是用来描述弹性介质各点应力状态的,后来发展成为力学和物理学的一个有力数学工具,目前力学方面的理论性文献都不同程度地这用了这一工具
由坐标原点和三条不共面的标架直线构成的坐标系称为直线坐标系,如果三标架直线上的单位尺度相同,称为笛卡尔坐标系,否则称为仿射坐标系。
笛卡尔坐标系又分为笛卡尔直角坐标系和斜角坐标系:三标架直线互相垂直时为笛卡尔直角坐标系,否则为笛卡尔斜角坐标系。
我们通常习惯用 x, y, z 三个坐标值来定义笛卡尔直角坐标系中的一点,以后我们将用x1,x2,x3 来分别代表 x, y, z,并简记为xi (i = 1, 2, 3)。
类似地用¯ij ( j = 1, 2, 3)表示三个坐标的单位矢量。下标 i , j ( j = 1, 2, 3)称为自由指标,它可用其它字母替代。无限定时,下标的取值均是1、2和3。
2.1.1 求和约定
在同一项中,如果某个下标重复出现两次,就表示要对这个指标从 1 到 3 求和,例如算式中有一项
AiBi
标 i 出现了两次,则应理解为:
AiBi=A1B1+A2B2+A3B3=3∑i=1AiBi
又如CmnDn,意义为
CmnDn=Cm1D1+Cm2D2+Cm3D3m=1,2,3
上式中 m 为自由指标,将其完全展开,则等同于下式:
C1nDn=C11D1+C12D2+C13D3C2nDn=C21D1+C22D2+C23D3C3nDn=C31D1+C32D2+C33D3
以后我们称重复出现的下标 i 为约定求和指标,约定求和指标在展开式中不再出现,因此也称为“哑指标”。
哑指标的字母可以更换成其它字母而不影响结果。
2.1.2 克罗内克(Kronecker)符号
δij={0,当 i≠j1,当 i=j
称为克罗内克(Kronecker)符号。
δij=δji
采用克罗内克(Kronecker)符号和约定求和方法,可使复杂公式的书写和运算简洁化。例如单位矩阵可表示成:
I=(100010001)=(δ11δ12δ13δ21δ22δ23δ31δ32δ33)=(δij)
又在笛卡尔直角坐标系中,两单位矢量的点乘可表示成:
→ii⋅→ij=δij
2.1.3 偏导数的下标记法
以后我们将记 ∂f∂xi 为f,i,∂2f∂xi∂xi记为 f,ij, 下标中的逗号即为导数记号。例如
∂Bij∂xk⇒Bij,kAi,i=∂Ai∂xi=∂A1∂x1+∂A2∂x2+∂A3∂x3
2.1.4 置换符号
∈ijk
置换符号又称 Permutation 符号,其定义为:
∈ijk=1,当i,j,k为1,2,3的循环序列;
∈ijk=−1,当i,j,k 为1,2,3的逆循环序列;
∈ijk=0 ,当i,j,k中有两个赋值相同时。
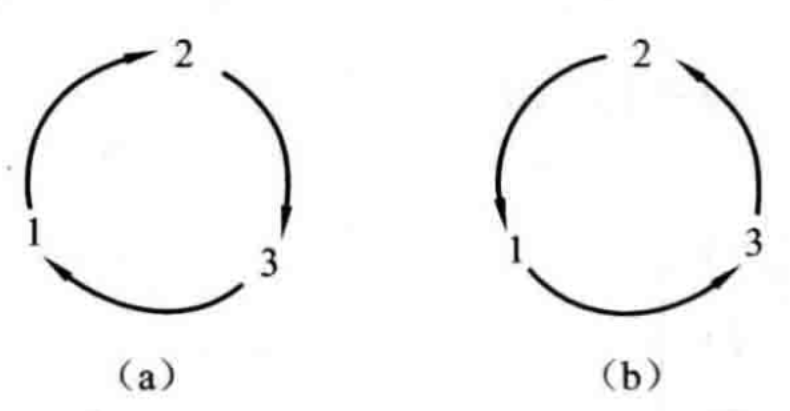
三个数字按下图(a)顺时针转时,有\1,2,3; 2,3,1; 3,1,2; \这种序列即称为循环序列,也称偶排列。
·三个数字按下图(b)逆时针转时,则为逆循\环序列, 也称奇排列,这时有\1,3,2;3,2,1;2,1,3。
利用置换符号可简化复杂表达式的书写,如可用置换符号表示三阶行列式的值:
|a11a12a13a21a22a23a31a32a33|=a11a22a33+a12a23a31+a13a32a21−a13a22a31−a11a23a32−a33a12a21=ϵijkai1aj2ak3=ϵijka1ia2ja3ki,j,k=1,2,3
练习:
1.化简
δijδjk=?δimBmj=?δijδij=?δimAm=?δii=?
-
将下式写成工程常用形式
εij=12(ui,j+uj,i)
-
将下式写成工程常用形式
εij=12Gσij−3μEσaδij上式中符号定义:G=E2(1+μ)σa=13σii=13(σ11+σ22+σ33)=13(σx+σy+σz)
练习答案
--
练习答案
\begin{aligned}
&\delta_{ij}\delta_{jk}=\delta_{i1}\delta_{1k}+\delta_{i2}\delta_{2k}+\delta_{i3}\delta_{3k}=\delta_{ik} \\
&\delta_{ij}\delta_{ij}=\delta_{1j}\delta_{1j}+\delta_{2j}\delta_{2j}+\delta_{3j}\delta_{3j} \\
&=\delta_{11}\delta_{11}+\delta_{12}\delta_{12}+\delta_{13}\delta_{13} \\
&+\delta_{21}\delta_{21}+\delta_{22}\delta_{22}+\delta_{23}\delta_{23} \\
&+\delta_{31}\delta_{31}+\delta_{32}\delta_{32}+\delta_{33}\delta_{33}=3 \\
&\delta_{ii}=\delta_{11}+\delta_{22}+\delta_{33}=3
\end{aligned}
$$\begin{aligned}
&\delta_{im}A_{m} =\delta_{i1}A_1+\delta_{i2}A_2+\delta_{i3}A_3 \\
&=A_i \\
&\delta_{im}B_{mj} =\delta_{i1}B_{1j}+\delta_{i2}B_{2j}+\delta_{i3}B_{3j} \\
&=B_{1j}\text{ ,}B_{2j}\text{ ,}B_{3j} \\
&=B_{ij}
\end{aligned}
\begin{gathered}
\varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}) \\
i=1,j=1 \\
\varepsilon_{11}=\frac{1}{2}(u_{1,1}+u_{1,1})=u_{1,1} \\
\varepsilon_x=\frac{\partial u}{\partial x}
\end{gathered}
\begin{aligned}
&&&\varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}) \\
&i=1,j=2 \\
&\varepsilon_{12}=\frac{1}{2}(u_{1,2}+u_{2,1}) \\
&\varepsilon_{xy}=\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial\nu}{\partial x}) \\
&&& \gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial\nu}{\partial x}
\end{aligned}
\begin{aligned}
&&& \varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}) \\
&i=1,j=3 \\
&\varepsilon_{13}=\frac{1}{2}(u_{1,3}+u_{3,1}) \\
&\varepsilon_{xz}=\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}) \\
&&&\gamma_{xz}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}
\end{aligned}
- 将下式写成工程常用形式
\varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,j})\quad\text{的工程常用形式}\\\varepsilon_{x}=\frac{\partial u}{\partial x}\quad\varepsilon_{y}=\frac{\partial\nu}{\partial y}\quad\varepsilon_{z}=\frac{\partial w}{\partial z}\\\varepsilon_{xy}=\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial\nu}{\partial x})=\frac{1}{2}\gamma_{xy}\\\varepsilon_{yz}=\frac{1}{2} (\frac{\partial\nu}{\partial z}+\frac{\partial w}{\partial y})=\frac{1}{2} \gamma_{yz}\\\varepsilon_{zx}=\frac{1}{2} (\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z})=\frac{1}{2} \gamma_{zx}
\begin{gathered}
\varepsilon_{ij}=\frac{1}{2G}\sigma_{ij}-\frac{3\mu}{E}\sigma^{a}\delta_{ij} \\
\text{上式中符号定义:}\quad G=\frac{E}{2(1+\mu)} \\
\sigma^{a}=\frac{1}{3}\sigma_{ii}=\frac{1}{3}(\sigma_{11}+\sigma_{22}+\sigma_{33})=\frac{1}{3}(\sigma_{x}+\sigma_{y}+\sigma_{z})
\end{gathered}
\begin{aligned}
&i=1,j=1& \varepsilon_{ij}=\frac{1}{2G}\sigma_{ij}-\frac{3\mu}{E}\sigma^{a}\delta_{ij} \\
&\varepsilon_{11}=\frac{1}{2G}\sigma_{11}-\frac{3\mu}{E}\cdot\frac{1}{3}(\sigma_{11}+\sigma_{22}+\sigma_{33}) \\
&\varepsilon_{x}=\frac{1+\mu}{E}\sigma_{x}-\frac{\mu}{E}\cdot(\sigma_{x}+\sigma_{y}+\sigma_{z}) \\
&\text{1} \\
&\varepsilon_{x}=\frac{1}{E}[\sigma_{x}-\mu\cdot(\sigma_{y}+\sigma_{z})] \\
&&\text{1} \\
&&\sigma^{a}=\frac{1}{3}\sigma_{ii}=\frac{1}{3}(\sigma_{11}+\sigma_{22}+\sigma_{33})=\frac{1}{3}(\sigma_{x}+\sigma_{y}+\sigma_{z})
\end{aligned}
\begin{aligned}&\varepsilon_{x}=\frac{1}{E}[\sigma_{x}-\mu(\sigma_{y}+\sigma_{z})]\\&\varepsilon_{y}=\frac{1}{E}[\sigma_{y}-\mu(\sigma_{z}+\sigma_{x})]\\&\varepsilon_{z}=\frac{1}{E}[\sigma_{z}-\mu(\sigma_{x}+\sigma_{y})]\\&\varepsilon_{xy}=\frac{1}{2G}\tau_{xy}\\&\varepsilon_{yz}=\frac{1}{2G}\tau_{yz}\\&\varepsilon_{zy}=\frac{1}{2G}\tau_{zx}\end{aligned}
2.2 张量的定义
张量 是由一组元素组成的一个整体,它在坐标变换时满足一定的关系。为便于理解张量的定义,先介绍坐标
轴旋转时空间一点的坐标变换关系。
图中两个坐标系原点相同,设原坐标系为 Qx_1x_2x_3,新坐标系为 Qx'_1x'_2x'_3,
旧坐标轴的夹角余弦
2.2 张量的定义
张量 是由一组元素组成的一个整体,它在坐标变换时满足一定的关系。为便于理解张量的定义,先介绍坐标
轴旋转时空间一点的坐标变换关系。
图中两个坐标系原点相同,设原坐标系为 Qx_1x_2x_3,新坐标系为 Qx'_1x'_2x'_3,
旧坐标轴的夹角余弦
\begin{array}
{|c|c|c|c|c|}
\hline &x_1&x_2&x_3\\
\hline x'_1&\beta_{11}&\beta_{12}&\beta_{13}\\
\hline x'_2&\beta_{21}&\beta_{22}&\beta_{23}\\
\hline x'_3&\beta_{31}&\beta_{32}&\beta_{33}\\
\hline
\end{array}
2.2 张量的定义
张量 是由一组元素组成的一个整体,它在坐标变换时满足一定的关系。为便于理解张量的定义,先介绍坐标
轴旋转时空间一点的坐标变换关系。
图中两个坐标系原点相同,设原坐标系为 Qx_1x_2x_3,新坐标系为 Qx'_1x'_2x'_3,
旧坐标轴的夹角余弦
研究一矢量\bar{P} ,其始端在原点,终端在旧系中的坐标为 x_i ,在新系中的坐标为x_i^\prime。
我们有
\begin{aligned}&x_{1}^{\prime}=\beta_{11}x_{1}+\beta_{12}x_{2}+\beta_{13}x_{3}\\&x_{2}^{\prime}=\beta_{21}x_{1}+\beta_{22}x_{2}+\beta_{23}x_{3}\\&x_{3}^{\prime}=\beta_{31}x_{1}+\beta_{32}x_{2}+\beta_{33}x_{3}\\
\\
&\text{即}x_{i}^{\prime}=\beta_{ij}x_{j}\end{aligned}
反过来也有
\begin{aligned}
&x_{1}=\beta_{11}x_{1}^{\prime}+\beta_{21}x_{2}^{\prime}+\beta_{31}x_{3}^{\prime} \\
&x_{2} = \beta_{12}x_{1}^{\prime}+\beta_{22}x_{2}^{\prime}+\beta_{32}x_{3}^{\prime} \\
&x_3 = \beta_{13}x_1^{\prime}+\beta_{23}x_2^{\prime}+\beta_{33}x_3^{\prime} \\
\\
&\textbf{即} \quad x_i=\beta_{ji}x_j^{\prime}
\end{aligned}
它在坐标变换时满足一定的关系 。
x_{i}=\beta_{ji}x_{j}^{\prime}\Rightarrow x_{j}=\beta_{kj}x_{k}^{\prime}\\x_{i}^{\prime}=\beta_{ij}x_{j}
x'_i=\beta_{ij}x_j=\beta_{ij}\beta_{kj}x'_k
\begin{gathered}
x_{i}^{\prime}=\beta_{i1}\beta_{k1}x_{k}^{\prime}+\beta_{i2}\beta_{k2}x_{k}^{\prime}+\beta_{i3}\beta_{k3}x_{k}^{\prime} \\
=\beta_{i1}(\beta_{11}x_{1}^{\prime}+\beta_{21}x_{2}^{\prime}+\beta_{31}x_{3}^{\prime}) \\
+\beta_{i2}(\beta_{12}x_1^{\prime}+\beta_{22}x_2^{\prime}+\beta_{32}x_3^{\prime}) \\
+\beta_{i3}(\beta_{13}x^{\prime}_1+\beta_{23}x^{\prime}_2+\beta_{33}x^{\prime}_3)
\end{gathered}
\begin{gathered}
x'_i=\beta_{i1}\beta_{k1}x_{k}^{\prime}+\beta_{i2}\beta_{k2}x_{k}^{\prime}+\beta_{i3}\beta_{k3}x_{k}^{\prime} \\
=\beta_{i1}(\beta_{11}x_1^{\prime}+\beta_{21}x_2^{\prime}+\beta_{31}x_3^{\prime}) \\
+\beta_{i2}(\beta_{12}x^{\prime}_1+\beta_{22}x^{\prime}_2+\beta_{32}x^{\prime}_3) \\
+\beta_{i3}(\beta_{13}x_1^{\prime}+\beta_{23}x_2^{\prime}+\beta_{33}x_3^{\prime}) \\
=(\beta_{i1}\beta_{11}+\beta_{i2}\beta_{12}+\beta_{i3}\beta_{13})x_{1} \\
+(\beta_{i1}\beta_{21}+\beta_{i2}\beta_{22}+\beta_{i3}\beta_{23})x'_2 \\
+(\beta_{i1}\beta_{31}+\beta_{i2}\beta_{32}+\beta_{i3}\beta_{33})x'_3
\end{gathered}
\begin{aligned}
&&x_{i}^{\prime}=\beta_{i1}\beta_{11}+\beta_{i2}\beta_{12}+\beta_{i3}\beta_{13})x_{1}^{\prime} \\
&&+(\beta_{i1}\beta_{21}+\beta_{i2}\beta_{22}+\beta_{i3}\beta_{23})x'_2 \\
&& +(\beta_{i1}\beta_{31}+\beta_{i2}\beta_{32}+\beta_{i3}\beta_{33})x'_{3} \\
&i=1: \\
&&\beta_{11}\beta_{11}+\beta_{12}\beta_{12}+\beta_{13}\beta_{13}=\beta_{11}^2+\beta_{12}^2+\beta_{13}^2=1 \\
&&\beta_{11}\beta_{21}+\beta_{12}\beta_{22}+\beta_{13}\beta_{23}=0 \\
&&\beta_{11}\beta_{31}+\beta_{12}\beta_{32}+\beta_{13}\beta_{33}=0 \\
&&\Rightarrow\beta_{ij}\beta_{kj}=\delta_{ik} \\
&类似地,有 \\
&&x_{i}=\beta_{ji}\beta_{jk}x_{k}&&&&& \Rightarrow\beta_{ji}\beta_{jk}=\delta_{ik}
\end{aligned}
2.2.2 张量的定义
张量元素的个数由空间的维数N及张量的阶数 n 决定, 即它等于N^n个,在笛卡尔坐标系中,N=3,下面我们给出 N=3 时各阶张量的定义。
1)零阶张量
零阶张量有N^0=3^0=1个元素,它是坐标变换的不变量,即
f^{\prime}(x_1^{\prime},x_2^{\prime},x_3^{\prime})=f(x_1,x_2,x_3)
这实际上是我们熟知的标量,是与坐标系无关的量。
- 一阶张量
一阶张量元素个数为N^1=3^1=3 ,设为T_i ,当坐标轴旋转时,它的变换规律
满足:
\begin{aligned}T'_i&=\beta_{ij}T_j\\\\\textbf{或}\quad T_i&=\beta_{ji}T'_j\end{aligned}
由定义可知一阶张量即我们熟知的 矢量
- 二阶张量
二阶张量元素个数为N^2=3^2=9 ,记为T_{ij},当坐标轴旋转时,它的变换规律
满足:
T^{\prime}{}_{ij}=\beta_{im}\beta_{jn}T_{mn}\\
\textbf{或}\qquad \qquad \qquad \quad \\
T_{ij}=\beta_{mi}\beta_{nj}T^{\prime}{}_{mn}
我们也可以这样来理解二阶张量变换系数的形成:
也可以这样来理解二阶张量变换系数的形成:有两个一阶张量A_i和B_j相乘,用A,每一个分量与B_{,}每一个分量相乘,共得到 9 个元素 ,用T_{ij}表示张量A_i和B_j相乘的结果有
T_{ij}=A_iB_j
写成矩阵形式便为:
\left.\left(T_{ij}\right)=\left(\begin{array}{ccc}A_1B_1&A_1B_2&A_1B_3\\A_2B_1&A_2B_2&A_2B_3\\A_3B_1&A_3B_2&A_3B_3\end{array}\right.\right)
当坐标变换时
A'_i=\beta_{im}A_m\quad B'_j=\beta_{jn}B_n
所以
\begin{aligned}
T_{ij}& =A'_iB'_j=\beta_{im}A_m\beta_{jn}B_n \\
&=\beta_{im}\beta_{jn}A_{m}B_{n} =\beta_{im}\beta_{jn}T_{mn}
\end{aligned}
二个一阶张量作上述张量乘积的运算也称为 并矢
- n 阶张量
n 阶张量有 N^n=3^n个分量,可用 T_{i_1i_2...i_n}表示,它随坐标的变换规律为:
T_{i_1i_2...i_n}=\beta_{i_1j_1}\beta_{i_2j_2}...\beta_{i_nj_n}T_{j_1j_2...j_n}\\
\text{或} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
T_{i_1i_2...i_n}=\beta_{j_1i_1}\beta_{j_2i_2}...\beta_{j_ni_n}T_{j_1j_2...j_n}
n 阶张量变换系数的来源也可按张量乘积的定义来理解 ,张量乘积的一般定义在下一节介绍。
为简单计,T_{i_1 i_2...i_n} 和 T^{\prime}_{i_1i_2...i_n}后面有时会记为T_{i_n} 和 T^{\prime}_{i_n}
3.2 张量的代数运算
下面内容适用于各阶张量,现以 黑体字 笼统地表示张量,而不涉及其具体阶次,同时介绍时略去证明过程。
-
张量的恒等
如果两个同阶张量的每个对应分量都相等,则称这两个张量相等。
根据张量的定义可知,在某一坐标系下,若两个张量相等,则变换到任一坐标系下这两个张量也必相等,即若有A=B,则必有A’=B’。
-
张量的加减
只有同阶张量才可以相加减,加减结果仍是同阶张量。若A、B是 n 阶张量,令其加减结果为C ,
则C也是 n 阶张量。
由张量的恒等与加减规则我们可得如下结论:若在某一笛卡尔直角坐标系中建立了张量方程
A-B=0
则当坐标轴旋转时总有
A’-B’=0
这表明张量方程在坐标变换时其形式不变.
进一步的研究表明上述结论对任意坐标系都是正确的,张量这一数学工具的重要性正在于此,它体现了 这 样的事实: :
任何物理规律都是客观存在的,与坐标系的选择无关。
分量方程 却不具有这一性质,在不同坐标系( ( 如笛卡尔直角坐标系、柱坐标系、球坐标系等) )中建立的 分量方程各不相同。
比如,弹性力学中以分量表示的平衡方程 :
笛卡尔直角坐标系下
\frac{\partial\sigma_{x}}{\partial x}+\frac{\partial\tau_{yx}}{\partial y}+\frac{\partial\tau_{zx}}{\partial z}+F_{x}=0 (\rho\frac{\partial^{2}u}{\partial t^{2}})\\\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_{y}}{\partial y}+\frac{\partial\tau_{zy}}{\partial z}+F_{y}=0 (\rho\frac{\partial^{2}v}{\partial t^{2}})\\\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}+\frac{\partial\sigma_{z}}{\partial z}+F_{z}=0 (\rho\frac{\partial^{2}w}{\partial t^{2}})
弹性力学中以分量表示的平衡方程 :
柱坐系下
\begin{gathered}
\frac{\partial\sigma_r}{\partial r}+\frac1r\frac{\partial\tau_{\theta r}}{\partial\theta}+\frac{\partial\tau_{zr}}{\partial z}+\frac{\sigma_r-\sigma_\theta}r+F_r=0 (=\rho\frac{\partial^2u_r}{\partial t^2}) \\
\frac{\partial\tau_{r\theta}}{\partial r}+\frac1r\frac{\partial\sigma_\theta}{\partial\theta}+\frac{\partial\tau_{z\theta}}{\partial z}+\frac{2\tau_{r\theta}}{r}+F_\theta=0 (=\rho\frac{\partial^2u_\theta}{\partial t^2}) \\
\frac{\partial\tau_{rz}}{\partial r}+\frac1r\frac{\partial\tau_{\theta z}}{\partial\theta}+\frac{\partial\sigma_z}{\partial z}+\frac{\tau_{rz}}r+F_z=0 (=\rho\frac{\partial^2u_z}{\partial t^2})
\end{gathered}
弹性力学中以分量表示的平衡方程 :
球坐标系下
\begin{aligned}
&\frac{\partial\sigma_{r}}{\partial r}+\frac{1}{r\sin\varphi}\frac{\partial\tau_{\theta}}{\partial\theta}+\frac{1}{r}\frac{\partial\tau_{\varphi r}}{\partial\varphi}+\frac{2\sigma_{r}-(\sigma_{\theta}+\sigma_{\varphi})+\tau_{\varphi r}\cot\varphi}{r}+F_{r}=0 (=\rho\frac{\partial^{2}u_{r}}{\partial t^{2}}) \\
&\frac{\partial\tau_{r\theta}}{\partial r}+\frac1{r\sin\varphi}\frac{\partial\sigma_\theta}{\partial\theta}+\frac1r\frac{\partial\tau_{\varphi\theta}}{\partial\varphi}+\frac{3\tau_{r\theta}+2\tau_{\varphi\theta}\cot\varphi}r+F_\theta=0 (=\rho\frac{\partial^2u_\theta}{\partial t^2}) \\
&\frac{\partial\tau_{r\varphi}}{\partial r}+\frac{1}{r\sin\varphi}\frac{\partial\tau_{\theta\varphi}}{\partial\theta}+\frac{1}{r}\frac{\partial\sigma_{\varphi}}{\partial\varphi}+\frac{3\tau_{r\varphi}+(\sigma_{\varphi}-\sigma_{\theta})\cot\varphi}{r}+F_{\varphi}=0 (=\rho\frac{\partial^{2}u_{z}}{\partial t^{2}})
\end{aligned}
平衡方程在不同坐标系中建立的分量方程各不相同
张量的乘积
若A是 m 阶张量,B是 n 阶张量,则我们用AB表示它们的乘积,其定义为:用前一个张量的每一个分量与后 一个张量的每一个分量相乘,共得3^{m}\cdot3^{n}=3^{m+n}它们构成的是m+n阶张量。
AB各元素指标的书写规定为:先写前一个张量的指标,保持其顺序不变,再写第二张量的指标,也保持其顺序不变。
例:A、B均是二阶张量,其分量分别为 A_{ij}、B_{mn} , 则A与B的乘积为四阶张量,用T 表示,T=AB, T的分量指标应书写成:
T_{ijmn}=A_{ij}B_{mn}
B_{i_1i_2...i_n}=\quad\lambda A_{i_1i_2...i_n}
B_{i_1i_2...i_n} 改成一个新的张量
A_{ijj}=A_{i11}+A_{i22}+A_{i33}
A_{ijj}只有三个元素,为一阶张量。
由张量的缩并运算定义可知, 缩并运算必需指明是对哪两个指标进行的 ,否则缩并运算的结果不是唯一的。
- 张量的内积
对张量A、B的乘积再进行一次缩并的联合运算,称为张量A、B的内积,记为:
C=A\cdot B
同一个张量对不同指标进行缩并,结果不同。
为了使张量内积的结果唯一,对张量内积中的缩并运算有如下进一步的规定:缩并的两个指标为前一个张量 的最后一个指标和后一个张量的第一个指标。
内积一般情况下不服从交换律,即
A\cdot B\neq B\cdot A
特殊情况如 B 是二阶张量,且B_{ij}=B_{ji}时交换律成立。
B_{ij}=B_{ji}时,称张量 B 为二阶对称张量
B_{ij}=-B_{ji}时,称张量 B 为二阶反对称张量
一个二阶张量一定可以唯一地分解成一个二阶对称张量和一个二阶反对称张量
2.5 张量的微分运算
在笛卡尔直角坐标系下,设张量分量在所定义的区域中是连续可微的,则张量的微分运算等于张量分量的直接 微分
例如对于坐标变换 x_i=\beta_{ij}x_j^{\prime} 有:
\frac{\partial x_i}{\partial x^{\prime}_j}=\beta_{ij}
参考文献





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· [翻译] 为什么 Tracebit 用 C# 开发
· 腾讯ima接入deepseek-r1,借用别人脑子用用成真了~
· Deepseek官网太卡,教你白嫖阿里云的Deepseek-R1满血版
· DeepSeek崛起:程序员“饭碗”被抢,还是职业进化新起点?
· RFID实践——.NET IoT程序读取高频RFID卡/标签