机器学习基础8--矩阵分解
用隐藏分解发现隐藏的数据结构
我们现在有一个用户对看过的电影的评分表
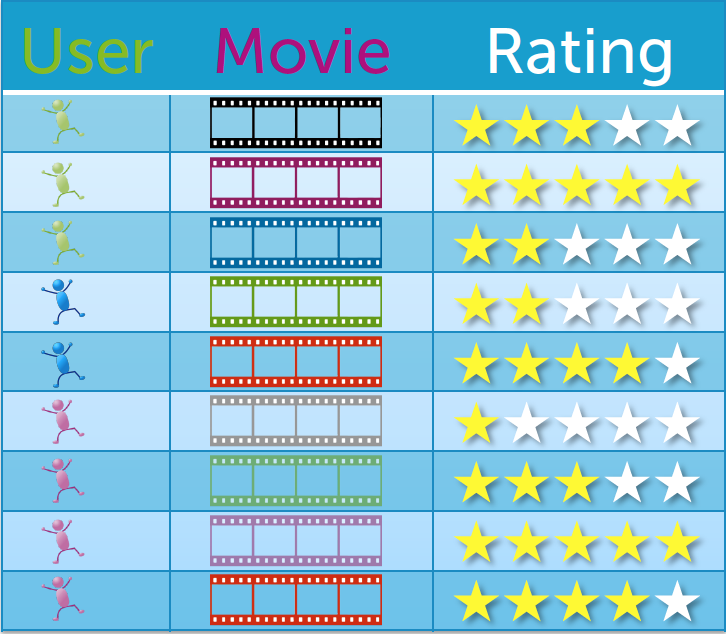
我们看到,绿色用户对3个电影做了评价,蓝色用户对2个电影做了评价,红色用户对4个电影做了评价.
但无论多少个用户,相对大量的电影来说,每个用户只有可能看过很少的一部分电影.
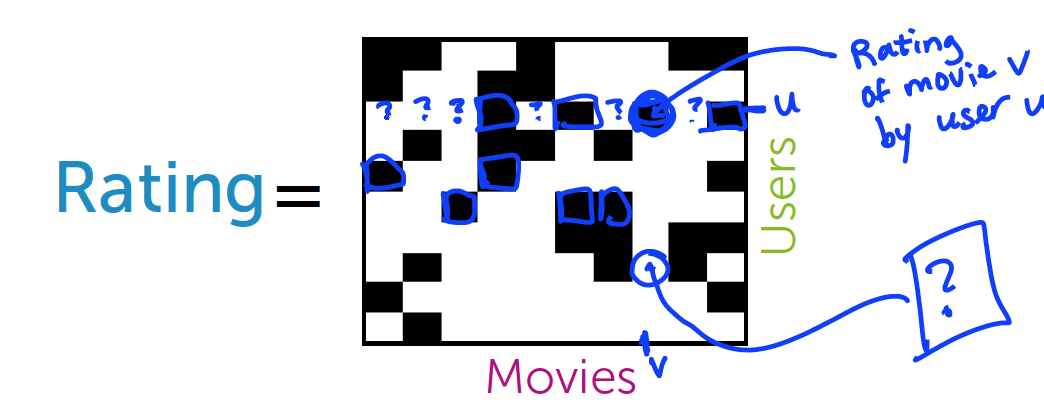
如上图所示,黑点代表了用户u对电影v的评价,白点代表该用户没有对电影进行评价.
那么我们如何填充未知数据?
利用该用户历史数据和所有用户对该电影的评价数据
预测一个人对从未看过的电影的评价:
我们需要用到2个向量:
电影类型向量:
假设
肖申克的救赎这部电影: 用动作相关值为0.3,与爱情相关值为0.01,与戏剧相关值为1.5
Rv = [ 0.3 0.01 1.5 ......]
用户偏好向量:
假设
用户A对电影的喜好:动作电影为2.5,爱情电影为0,戏剧电影为0.8
Lua = [ 2.5 0 0.8 ......]
那么Rating(u,v)的值为
0.3 * 2.5 + 0 + 1.5 * 0.8 + ...... = 7.2
假设B用户的Lub为 [ 0 3.5 0.01 ...... ]
0 + 0.01*3.5 + 1.5*0.01 + ...... = 0.8
很明显,A用户喜好这部电影的可能性更大.
当然,一个电影最高评分为5分, 7,2显然没有体现分数的预测.
上面的方法显然可以预测出用户对电影的评价情况,但是有一个最主要的问题.
我们并不知道所有的Lu和Rv
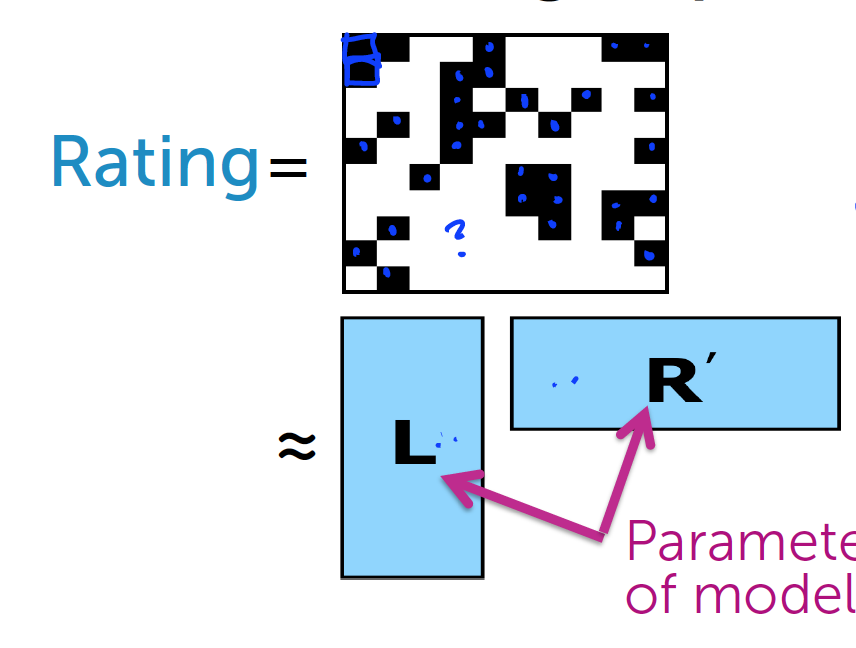
我们需要用到矩阵因子分解模型:
仍然使用残差平方和:
RSS(L,R) = (Rating(u,v) - <Lu,Rv>)2 + [ include all (u,v) ]
注意:后面中括号内的u,v指的是所有已经做出评价的u,v
但是,这个模型我们仍然会遇到冷启动问题.
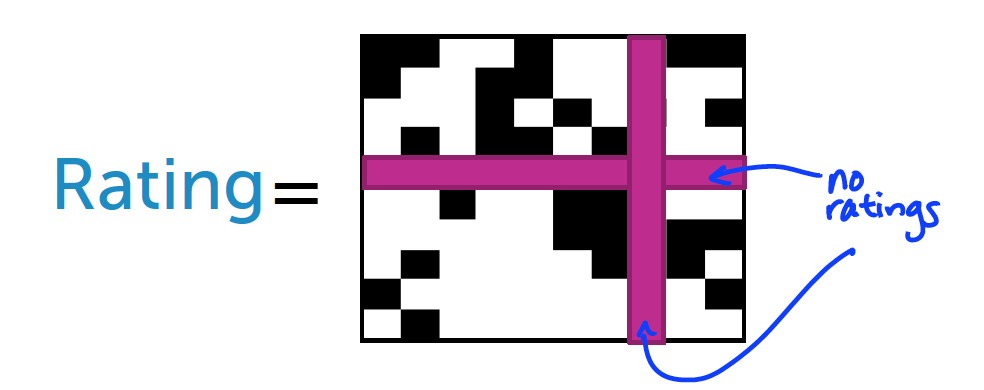
如何评价模型的性能:
精度和召回率
召回率:
#liked & shown / #liked
精度
#liked & show / #shown
如果所有商品都进行推荐,召回率变成了1,但是精度变得非常小.
最佳的性能: 精度 = 1,召回率 = 1
不同算法之间进行比较:
曲线下的面积最大的,就是最优性能
end
课程:机器学习基础：案例研究(华盛顿大学)
视频链接: https://www.coursera.org/learn/ml-foundations/lecture/1Blxo/the-matrix-completion-task
