机器学习基础1--线性回归
定义:
线性回归(Linear Regression)是利用线性回归方程的最小平方函数,对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
案例:
房价预测
目标:
房屋大小(X)和价格(Y)之间的关系
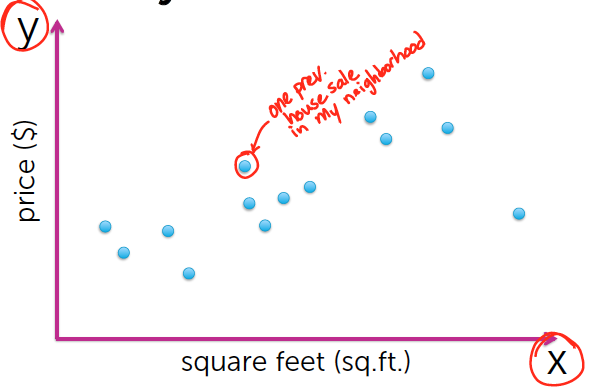
如图所示,我们将房屋价格Y,与房屋大小X,绘制在坐标系.
在这里会引入新的定义:
X:特征,协变量,自变量
Y:观测值,因变量
很明显,在很大概率下,我们无法从一个随机的X下,找到Y的对应值.
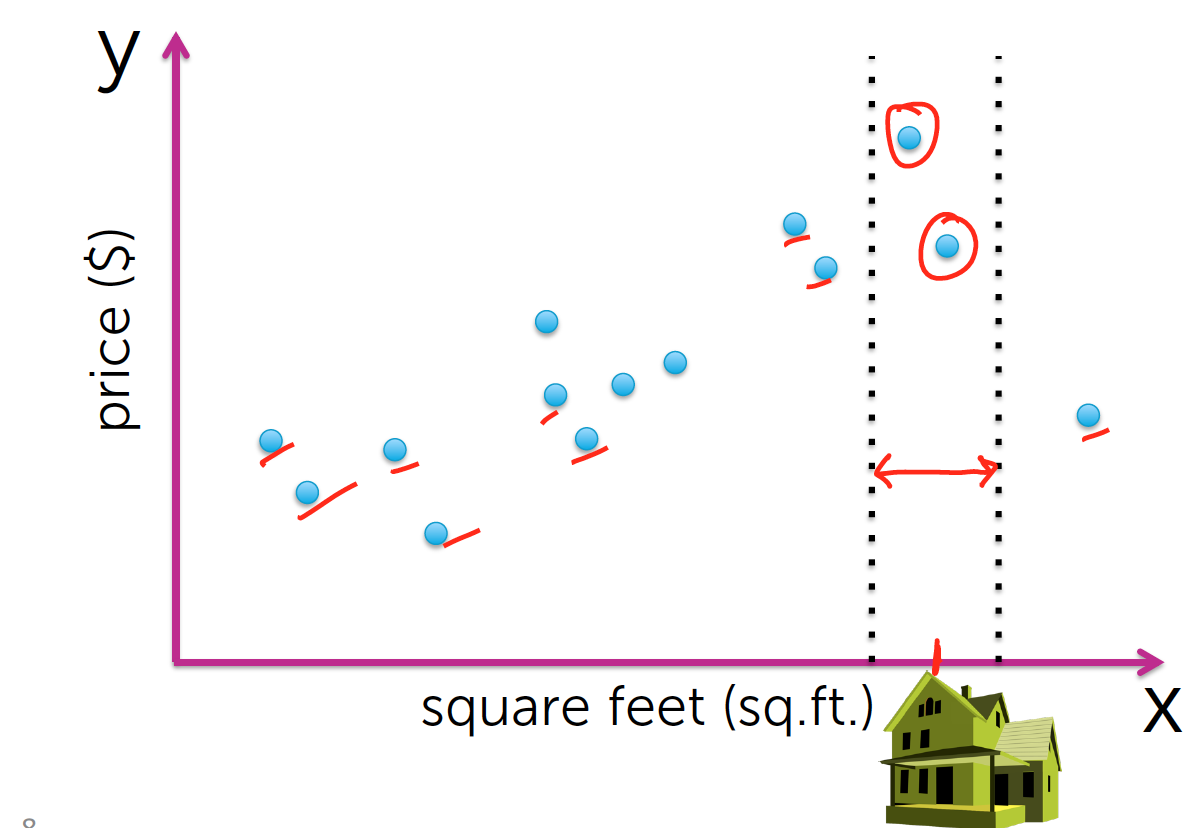
如此,我们取我们的房子大小两边的两个价格,来对房屋价格进行判断.但这会带来另一个问题,难道房屋的价格,只和图中圈起来的2个点有关,与其他值无关?那我们收集这么多数据有何用处?
线性回归:
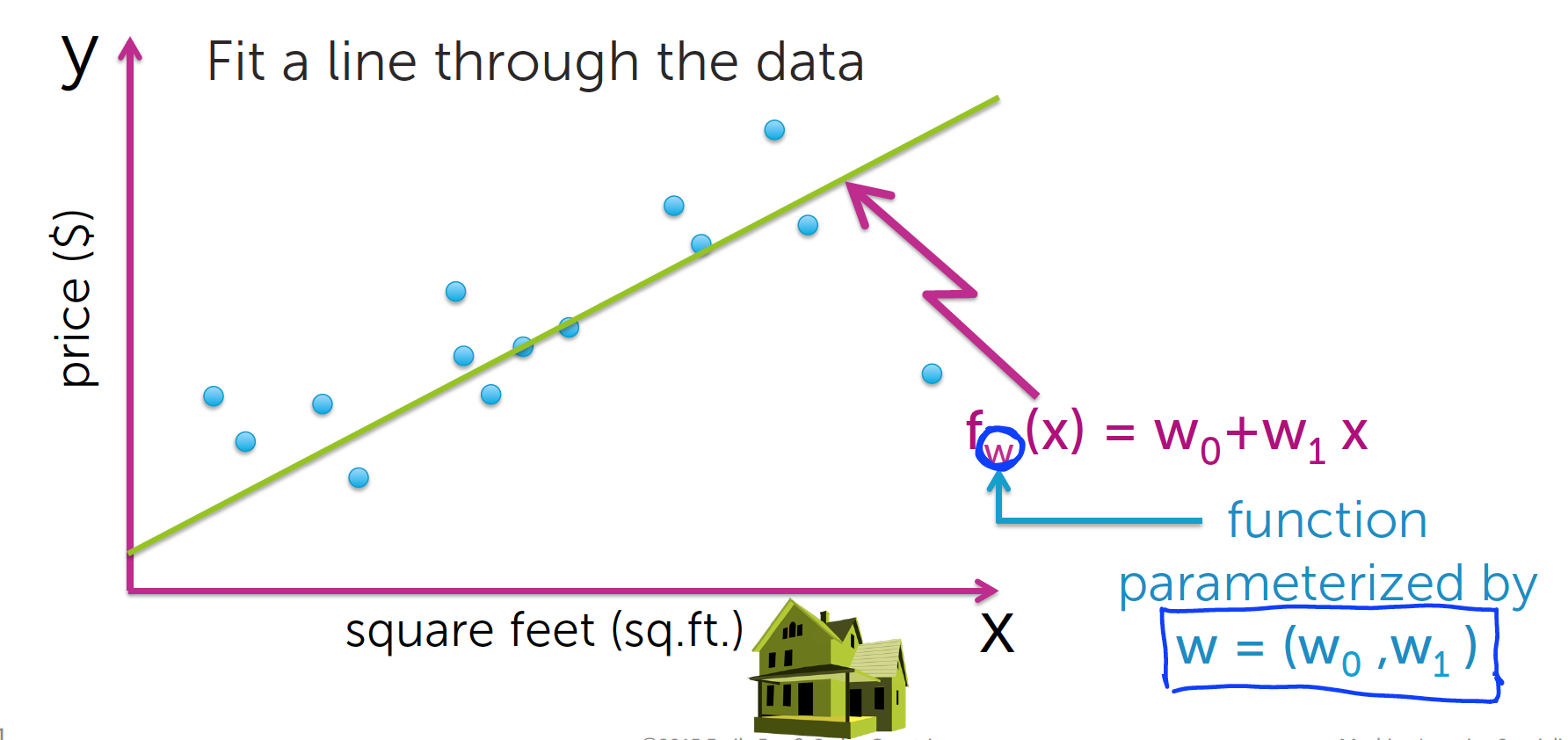
如图所示,我们尽量穿过最多的值(这种说法并不准确),画出一条直线,那么这条直线的公式为
fw(x) = w0 + w1x
w0:截距
w1:斜率
w:函数的参数
注意:通常把W1称作特征X的权重.
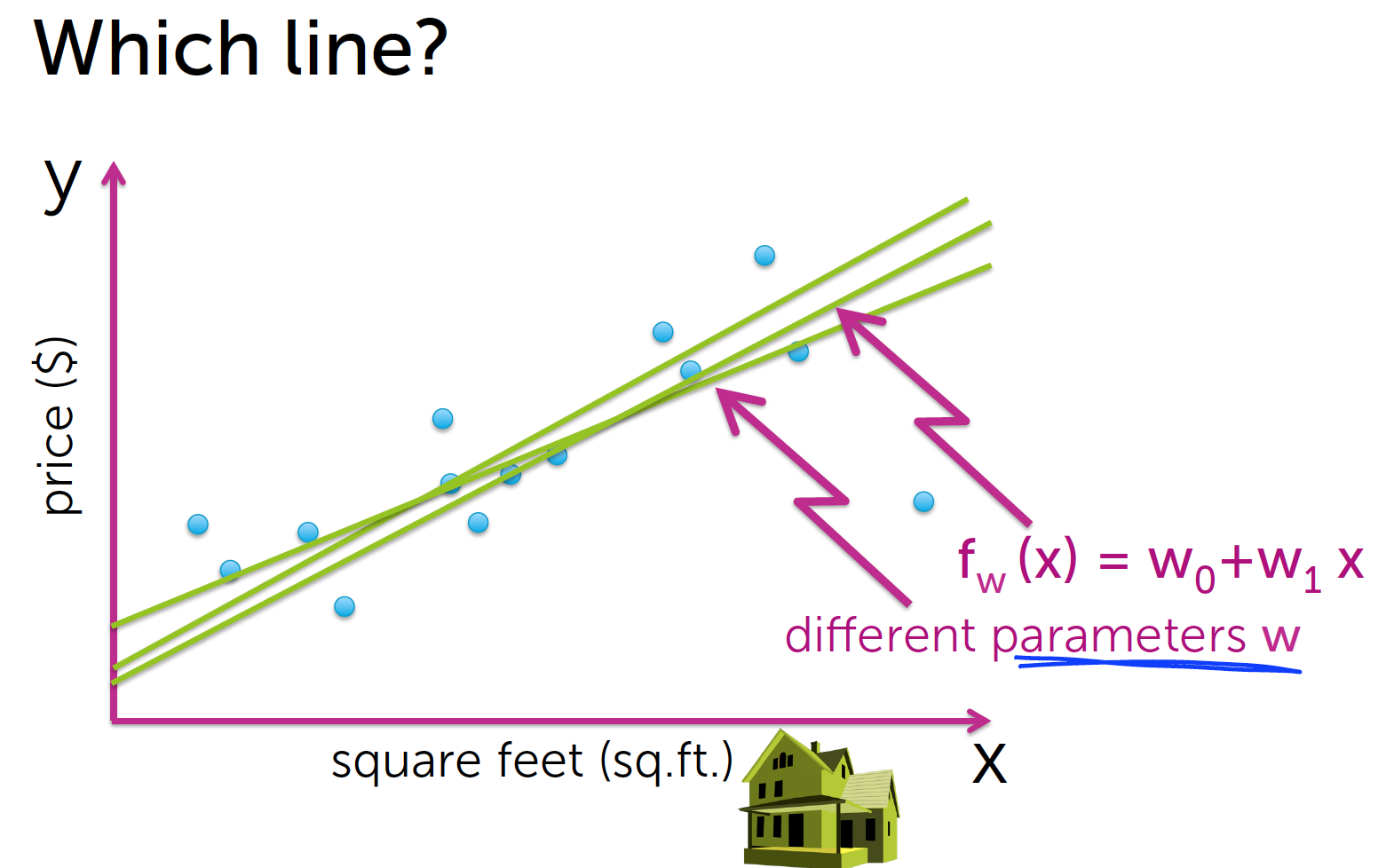
很明显,这种直线有很多,不同的参数w会形成不一样的直线,我们应该选择哪条?
残差平方和

计算每个点到直线的距离,将其平方值相加,得到残差平方和.
残差的含义:表示着预测值和真实数据的值差了多少
那么在多条线的情况下,w0组成一个集合W0_hat,w1组成一个集合W1_hat,相应的,w也组成一个集合W_hat(为了书写方便我直接使用了_hat,实际应写作ŵ)
W_hat = (W0_hat,W1_hat)
fŵ(x) = ŵ0 + ŵ1 x
那么计算你自己房价价格的公式:
ŷ = ŵ0 + ŵ1 Size_of_house
那么,你有一个数学系的研究生朋友,你把你的分析结果跟他说了.
他说,这不是一个线性关系,试试二次函数?
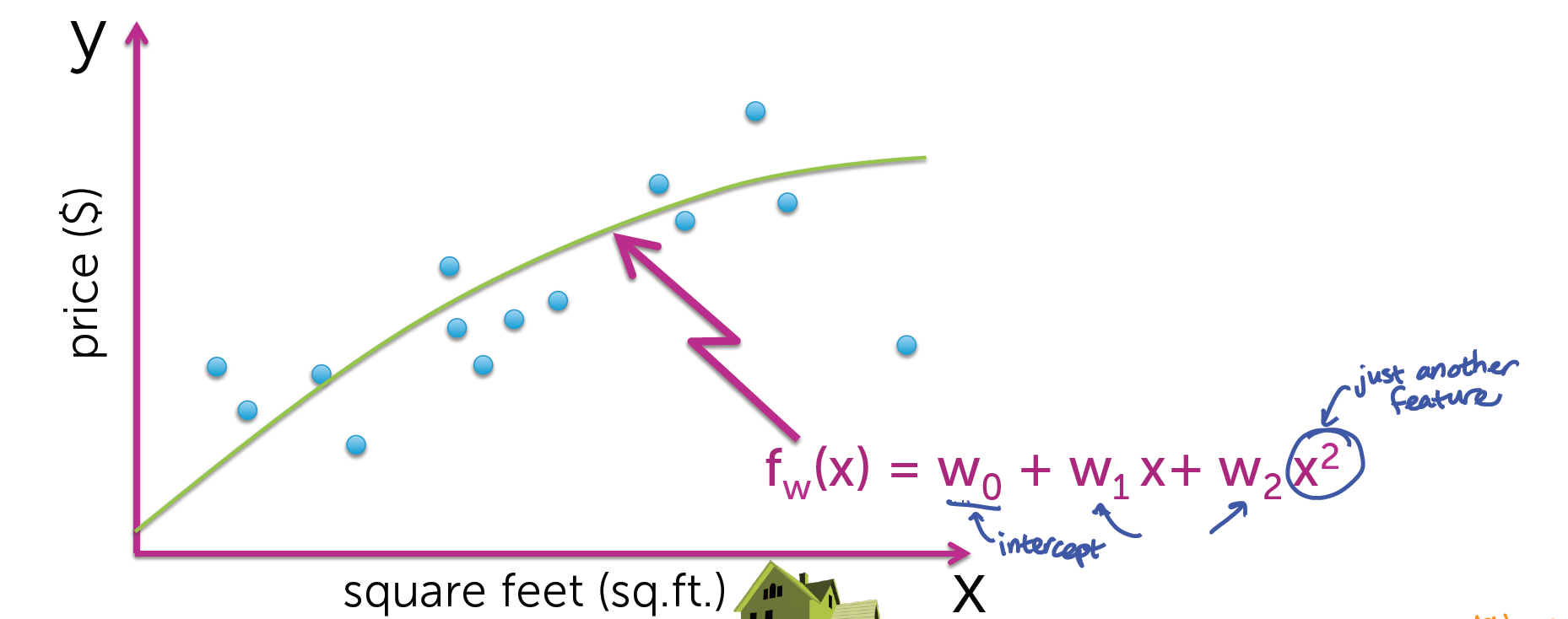
注意:这仍然是一个线性回归,我们可以把x2认为是另一个回归量.
你朋友又说了,我可以最小化你的残差平方和,来个13次函数!
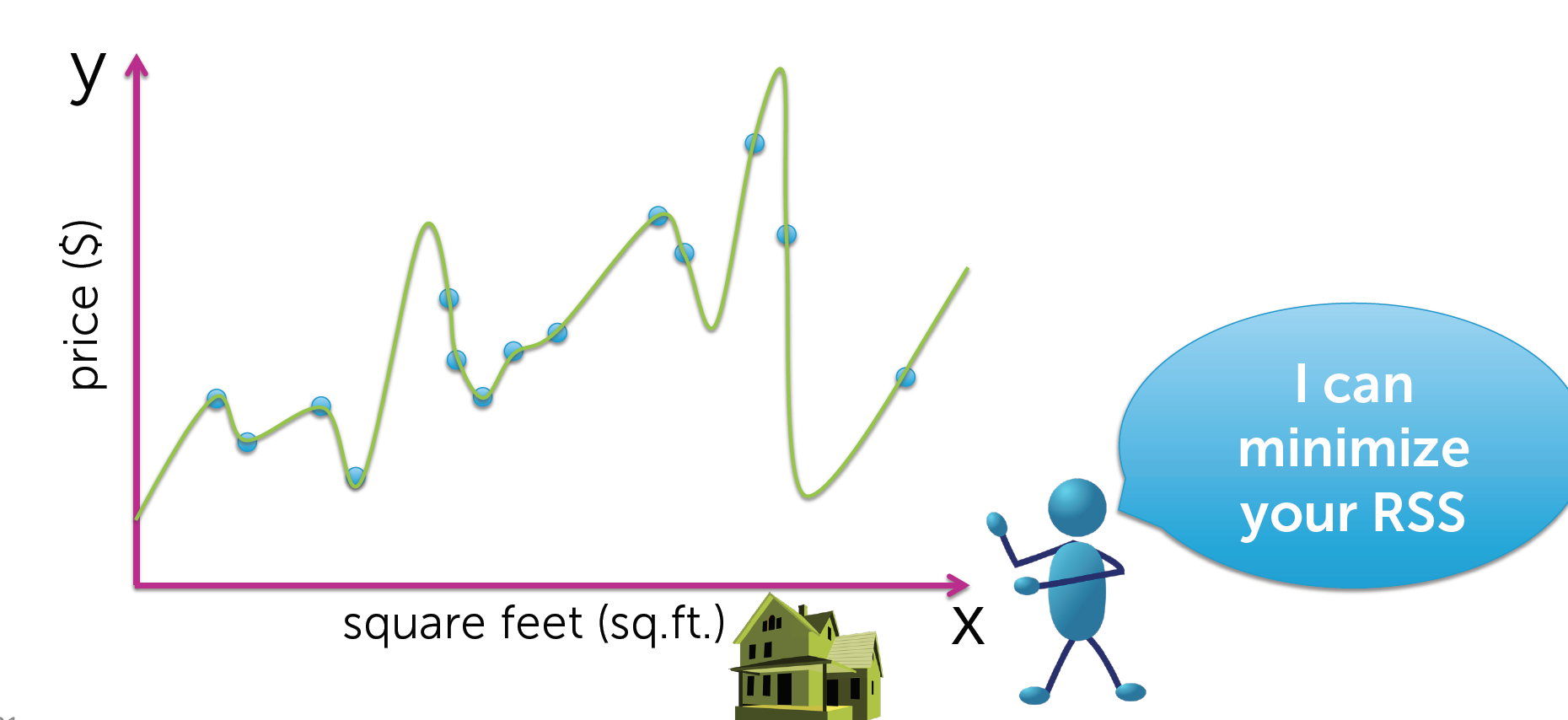
WTF???还有这种操作!
就是我的房子怎么才这么点钱?
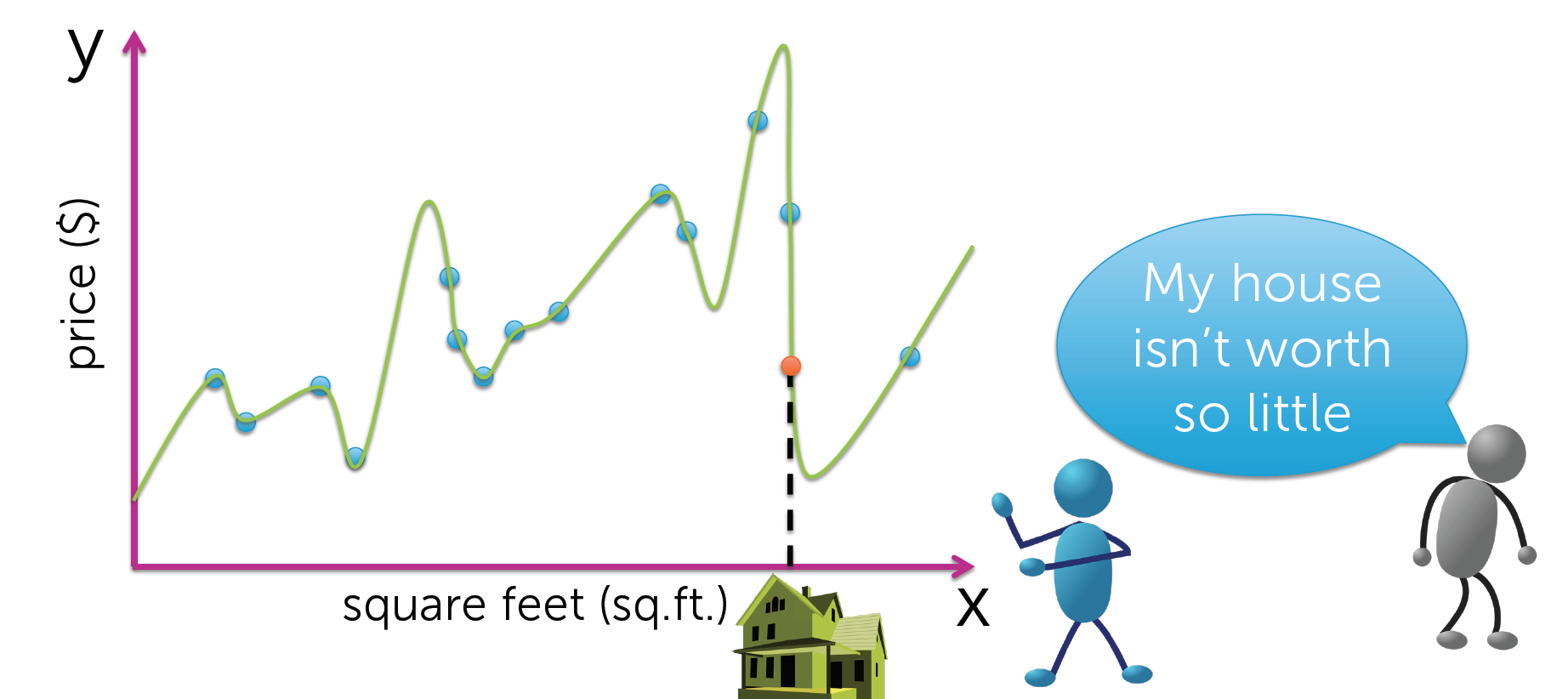
这种现象称为过拟合.
end
课程:机器学习基础:案例研究(华盛顿大学)
视频链接:https://www.coursera.org/learn/ml-foundations/home/welcome
week2 Linear regression modeling




