矩阵乘法及简易公式推导

矩阵乘法

　　矩阵加法很简单，结果矩阵的某一位置上的数就是加数矩阵对应位置上的数之和。如下图：

 

 

 

　　那矩阵乘一个数呢？把矩阵每一个位置上的数都乘上那个数就得到了结果矩阵。如下图：

　　可以发现矩阵乘一个数可以当成乘法分配律来理解。

 

　　那矩阵乘矩阵呢？还按对应位置相乘吗？

　　起初，矩阵的作用是表示线性代数方程组，如下图：

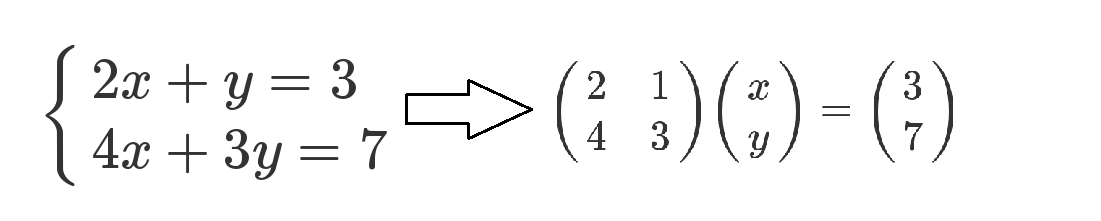
　　从图中可以看出，左矩阵每一行第N列位置上的数乘上右矩阵第N行位置上的变量就等于结果矩阵中第N行的数。这样左矩阵每一行都构成一个方程，最终组成一个方程组。

　　现在我们可以开始推导矩阵乘法的公式了。

　　首先我们可以定义一个用矩阵A表达的线性方程组。如下图：

　　再定义一个矩阵B表达 x 与 t 的关系。如下图：

　　很显然，我们可以把B矩阵带入到A矩阵，以及把B表达的方程组带入到A表达的方程组。如下图：

　　代入得到的方程组括号拆开后提出来t1和t2，可以化简得到一个新方程组。如下图：

　　由矩阵和线性代数方程组的关系得出：

　　

　　将上图中的式子与之前推导出的式子（下图）相比较：

　　可以得出：

　　

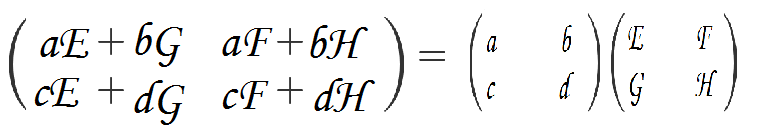
　　这也就是矩阵乘法的行列规律，即结果矩阵M行N列位置的数为左矩阵M行的数按次序对应乘上右矩阵N列相应次序的数，得到的所有积的总和。从这也可以看出相乘的两个矩阵必须满足一个矩阵的行数等于另一个矩阵的列数。