D3算法编写决策树

 前言

所谓构建决策树，

就是递归的对数据集参数进行“最优特征”的选择。然后按最优特征分类成各个子数据集，继续递归。

最优特征的选择：依次计算按照各个特征进行分类以后数据集的熵，各个子数据集的熵比较后，其中拥有最小的熵的数据集就是最优的分类结果，此次分类的特征就是最优特征。

熵的计算：熵计算的是数据集的纯净程度，数据集的熵的大小只和数据集中各数据样本的最终分类结果的分布有关。假设数据集中所有数据都是“同一种类”的数据，那么其熵就是0，表示是最纯净的数据。

（所以最优特征的选择就变成了，先计算分类前的数据集的熵，再计算按某种特征分类后其各个子数据集的熵的期望，然后取原数据集熵与分类后的熵期望之差作为评价分类效果的标准。）

（此处之所以计算分类后所有子数据集的熵的期望其实很好理解。期望也可以看成一堆离散数据的平均值，假设我们把原数据集分成了三堆子数据集，这三堆子数据集哪一堆也不能代表分类后的结果，只有三堆总结果再求个期望也就是三堆的平均值，才能代表分类后的结果）

 

 

熵的计算

我们用数据集中各结果分类出现的概率来作为计算熵的决定因素。

假设整个样本数据集中样本都有着“统一的分类结果”时，出现该分类结果的概率是100%，其熵就是0。

而如果数据集中有10个样本，每个样本都有一个独立的结果分类，那么出现每一种结果的概率都是10%，这种结果的不确定性自然要比上一个大（上一个可是100%的确定结果），其最终熵值肯定也要更大。

 

至此我们可以看出，我们需要找到一个函数能把事件出现的概率映射成熵值。

这个函数就是以下这个函数

 

其函数图像为

 

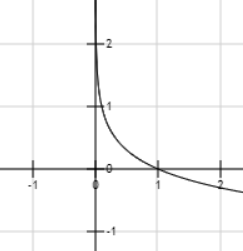
x轴是事件出现的概率

y轴是熵的值

 

通过图像我们可以看出随着事件出现的概率越来越大，熵也越来越小，直至到0。

 

假设数据集中一共有出现三种分类结果的可能，该数据集的熵自然是算出这三种分类结果的熵后在求其三者的期望，使用期望作为该数据集的熵。

 

python代码实现如下：

from math import log

"""
数据集，
二维数组中的前三个元素都是特征，
最后一个元素是样本的分类结果。
"""
data = [["有眼镜", "短发", "胖", "男"],
        ["有眼镜", "长发", "瘦", "女"],
        ["有眼镜", "短发", "胖", "女"],
        ["没眼镜", "长发", "胖", "男"],
        ["没眼镜", "短发", "瘦", "男"]]

"""
data：需要计算熵的数据集
return：该数据集的熵

计算数据集的熵
"""
def calcShannon(data):
    # 熵
    shannonMean = 0
    # 数据总量
    sumDataNum = len(data)
    # 数据集的所有分类情况
    classify = [man[-1] for man in data]
    # 循环每一种分类结果，计算该分类结果的熵，并求期望
    for resClassify in set(classify):
        # 该分类结果的“发生”概率
        p = classify.count(resClassify) / sumDataNum
        # 计算该分类结果的熵
        shannon = -log(p, 2)
        # 求期望
        shannonMean += p * shannon
    return shannonMean

print(calcShannon(data))

 

构建决策树

我们的最终目的是要构建出下图结构的决策树。

 

 

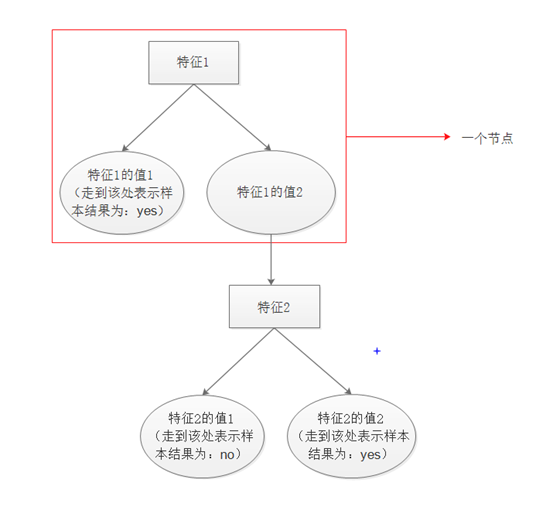
上图转换成python字典数据格式为：

{特征1：{值1：yes，值2：{特征2：{值1：no，值2：yes}}}}

 

完整python代码如下：

from math import log

"""
数据集，
二维数组中的前三个元素都是特征，
最后一个元素是样本的分类结果。
"""
data = [["有眼镜", "短发", "胖", "男"],
        ["有眼镜", "长发", "瘦", "女"],
        ["有眼镜", "短发", "胖", "女"],
        ["没眼镜", "长发", "胖", "男"],
        ["没眼镜", "短发", "瘦", "男"],
        ["有眼镜", "长发", "瘦", "女"],
        ["有眼镜", "长发", "胖", "男"]]

"""
样本参数中各个特征的描述信息
"""
labels = ["是否戴眼镜", "头发长短", "身材"]

"""
计算数据集的熵

data：需要计算熵的数据集

return：该数据集的熵
"""
def calcShannon(data):
    # 熵
    shannonMean = 0
    # 数据总量
    sumDataNum = len(data)
    # 数据集的所有分类情况
    classify = [man[-1] for man in data]
    # 循环每一种分类结果，计算该分类结果的熵，并求期望
    for resClassify in set(classify):
        # 该分类结果的“发生”概率
        p = classify.count(resClassify) / sumDataNum
        # 计算该分类结果的熵
        shannon = -log(p, 2)
        # 求期望
        shannonMean += p * shannon
    return shannonMean


"""
统计分类数组中出现最多的项，并返回该项的值
"""
def statisticsMostClassify(classify):
    map = {}
    for resClassify in classify:
        value = map.get(resClassify)
        if value:
            map[resClassify] = value + 1
        else:
            map[resClassify] = 1
    mostClassify = sorted(map.items(), key=lambda item: item[1])
    return mostClassify[-1][0]


"""
对数据进行分类，并返回分类后的结果（如按照a特征分类后，分类后的结果数据集中就没有a特征值了）

index：按照第几个特征开始分类，从0开始
value：按照该特征的什么值进行分类
data：待分类数据
"""
def categorizationOfData(index, value, data):
    resData = []
    # 循环每一个样本，如果第index个特征的值符合指定特征，就把该特征删除后保存
    for man in data:
        if man[index] == value:
            tmpMan = man[:]
            tmpMan.pop(index)
            resData.append(tmpMan)
    return resData


"""
D3算法构建决策树
步骤：
0、获取数据集
1、判断当前数据集是否需要继续分类，如不需要，则返回结果分类
2、找到最优特征
3、根据最优特征进行分类，并把最优特征删去
4、
"""
def createTree(data, labels):
    classify = [man[-1] for man in data]
    # 如果当前数据集数据都是同一分类结果则不用继续分类
    if len(set(classify)) == 1:
        return classify[0]

    # 如果数据集中的样本没有特征了，则返回数据集中出现最多的分类结果
    if not labels:
        return statisticsMostClassify(classify)

    # 原数据集香农熵
    originalShannon = calcShannon(data)
    # 熵差
    diffShannon = 0
    # 最优特征（index下标）
    bestFeatureIndex = 0
    # 按照最优特征分类后的结果{分类结果值：分类后的数据集}
    bestClassifyData = {}
    # 循环计算按照每一个特征分类后的结果，选择其中使得熵差值最大的特征作为最优特征
    for i in range(len(labels)):
        tmpClassifyData = {}
        # 取出第i个特征的所有可能值
        valueAll = [man[i] for man in data]
        valueSetAll = set(valueAll)  # 去重后的所有可能特征值
        # 循环计算按各个可能值分类后的熵，然后求期望
        classifyShannonMean = 0
        for value in valueSetAll:
            resData = categorizationOfData(i, value, data)  # 按该特征值分类后结果
            classifyShannon = calcShannon(resData)  # 分类后的熵
            classifyShannonMean += (valueAll.count(value) / len(valueAll)) * classifyShannon  # 期望
            tmpClassifyData.update({value: resData})
        # 计算按照当前特征分类后的熵差
        diff = originalShannon - classifyShannonMean
        if diff >= diffShannon:
            bestFeatureIndex = i
            bestClassifyData = tmpClassifyData
            diffShannon = diff
    # 按结果分类，把labels中的最优特征删去，构建节点，并将各结果数据集递归
    bestFeature = labels[bestFeatureIndex]  # 获取最优特征的中文描述
    tmpLabels = labels[:]
    tmpLabels.pop(bestFeatureIndex)
    node = {bestFeature: {}}  # 当前节点
    for key in bestClassifyData:
        resClassify = createTree(bestClassifyData[key], tmpLabels)
        node[bestFeature].update({key: resClassify})
    return node

# 使用样本测试样本构建决策树
tree = createTree(data, labels)
# 打印树
print(tree)
# 得到结果：{'是否戴眼镜': {'有眼镜': {'身材': {'胖': {'头发长短': {'长发': '男', '短发': '女'}}, '瘦': '女'}}, '没眼镜': '男'}}

 

（ps：不知不觉已经是第100篇随笔了，还是很有成就感的^_^）