决策树

前言

构建决策树的前提：

与之前讲的那些回归算法一样，如果想要构建一颗决策树，首先你手里得有大量的已经知道结果的样本数据。

比如你想通过决策树来分析一个人是否是罪犯，那么你手里就必须得有一定量的人类样本。并且还得从这些人类样本身上提取出各种用于分类的特征，如是否有纹身、学历高低、是否有刀疤等。

然后就是通过这些已经知道结果的样本参数来构建决策树。

 

决策树算法的整个过程如下：

1、创建一个根节点，把所有数据都放在根节点，然后选择一个最有特征，之后按照这个最优特征对所有数据进行分类。

2、判断每个子集有没有被正确分类，如果正确分类，那么就为该子集建立叶子结点，把这些子集放到叶子结点里。如果没有被正确分类，则继续选择子集的最优特征，然后将子集按最有特征分隔。

递归整个2阶段，直至所有数据都被正确分类。

 

决策树的算法主要包含三个部分：

特征选择：特征选择的目的是“选取能够最优的将数据集进行分类的特征”，特征选择的关键是：信息增益、信息增益比、Gini指数。

决策树的生成：通常利用：信息增益最大、信息增益比最大、Gini指数最小作为准则。从根节点递归生成决策树。

决策树的剪枝：剪枝的目的是为了防止树过拟合。剪枝包括预剪枝和后剪枝。

 

由此可看出主要要解决的问题是：

1、最优特征如何选择？

2、如何判断数据有没有被“正确”分类？

 

最优特征的选择

所谓最优特征，就是指这个特征拥有最好的分类能力，而衡量其分类是否分的好的标准就是“信息增益”。

所谓信息增益，就是指：对数据进行分类之前与之后数据信息发生的变化。如果分类之后这个信息增益很大，就证明分类分的很好（换句话说通过这个分类的确把信息按一种很大的差异分开了），这时这个分类特征就是当前状态下的最优特征。

 

所谓信息增益，说明白点就是分类以后信息的价值增加了多少。

而信息的价值是用“熵”这个概念来衡量的。

熵代表了事物的混乱程度，熵越大表示事物越混乱，其价值也越低。

所以信息增益的计算就变成了：分类前后其熵“减少”了多少？

分类前后其熵的差值越大，表示熵减少的越多，信息越稳定，价值也就变高了。

 

信息熵

之前说了熵代表了事物的混乱程度（或者说是不确定度），熵越大表示事物越混乱。

在信息熵中，“信息的价值是通过信息的传递体现出来的，传播的越广、流传时间越长的信息越有价值”。

所以信息的某种情况出现的概率越高，其对应的熵值也越低，比如信息的某种情况发生的概率为100%，那么其自然就是个很肯定的事件，混乱程度也为0，熵就是0.

由此可见熵应该随着事件的发生概率增大而减小。

 

“只有一个不确定变量的信息的熵”的公式为：

 

其中P是某一个不确定变量出现的概率，图像如下

 

 

整个公式图像为递减函数，且自变量P的取值肯定是在[0,1]之间，随着信息出现概率越大，其熵也越小，当事件出现概率为100%时，其熵自然为0，即混乱程度为0，是个很肯定的事件。

 

而一般情况下每一种信息都会包含多种可能值，

如：学生上课睡觉是一种信息，其包含的可能值就有两种：睡和不睡。

而之前也说了，熵的计算需要信息出现的概率。

假设我们以一个50人班的某一节课为背景，其中20个人睡觉了，30个人没睡。

那么上课睡觉这个信息就有两种数值：20人睡、30人没睡。

其反映出来的概率就是P(睡) = 2/5 P(没睡) = 3/5

 

但我们要算的是“上课睡觉这个信息”的熵，我们需要求一个信息那么就需要对该信息拥有的“所有可能值的出现值”求数学期望，找到一个所有值的平均表达。

（期望：

假设我们要求某一事件的期望。

首先要分析该事件有多少种可能的结果。

所谓期望就相当于是这些结果的一个平均结果。

期望 = 各结果出现的概率乘上各结果的结果值，然后相加。

例：

事件：某个城市中每个家庭小孩的个数

该事件的可能结果：0个小孩、1个小孩、2个小孩、3个小孩

期望：这个城市中每个家庭小孩的个数的平均值（即每个家庭平均有多少小孩）

假设0个小孩的家庭在该城市中占1%，1孩占90%，2孩占6%，3孩占3%（可以看出各种孩子数的概率构成了一个完备事件组），

则：

 

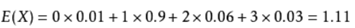
说明每个家庭平均有1.1孩。）

于是我们熵的真正计算公式如下

 

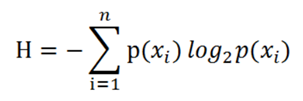
H是信息的“平均熵”，也就是该信息的平均混乱程度。

 

之前我们也说了，我们最终的目的是要求出“信息增益”，而信息增益指的是：对数据进行分类之前与之后数据信息发生的变化。如果分类之后这个信息增益很大，就证明分类分的很好。

之前我们已经推导出了：信息在任意一时刻的“熵”的计算公式。

所以我们现在需要计分类前的熵和分类以后的熵。然后用“分类前的熵”减去“分类后的熵”，其差值就是混乱程度减小的量，即信息增益，这个增益自然是越大越好。

（之所以用分类前减分类后，是用为分类的目的就是减少信息的混乱程度，分类前的熵自然比分类后的熵要大。而这个混乱程度减少的越多自然分类分的越好。）

 

经验熵

经验熵可以看成是“分类前的熵”。

 

假设我们最后是要通过决策树预测“某人是否是罪犯”。

我们现在手上有100个人作为样本。

可以从这100个人中提取出：是否有纹身、是否有刀疤、学历高低等各种特征。

而且我们也知道了，通过各种特征组合后，100人里，40个是罪犯，60个是好人。

 

熵指的是信息的混乱程度。

而经验熵也是一种熵，是我们手头上所有样本的“最终分类结果”这一信息的混乱程度。

（我们希望通过每次的分类，使得最终分类结果这一信息混乱度最低）。

而在这个例子里，我们最终分类的目的是判断“某人是否是罪犯”，所以我们每次分类前的经验熵都是计算“某人是否是罪犯”这一信息的熵。

某人是否是罪犯这个信息一共有两种可能结果：是、不是。根据之前的推导我们乣计算所有可能结果的熵的期望。

所以“某人是否是罪犯”这一事件的熵为：

H(D) = - [40/100*log2(40/100) + 60/100*log2(60/100) ]

 

由此经验熵公式可以写成：

 

|D|表示样本总容量。

|Ck|表示“满足第k种可能性”的样本的个数。

此时的H(D) 指的就是“最终分类结果”的熵。

 

条件熵

条件熵可以看成是“分类后的熵”。

 

我们分类前与分类后其实只关注“分类的最终结果”这一信息的熵的值（因为得到最终分类结果才是我们建立决策树的最终目的）。

还是用上面判断罪犯的例子，在分类前，我们计算的是“最终样本是否是罪犯”这一特征。

分类后，我们应该还是关注“样本是否是罪犯”这一特征。

所以，我们需要知道“按某种特征分完类以后，样本的最终分类情况的熵改变了多少”。

 

条件熵就是“以某一特征分类后”的样本的最终结果情况的熵。

（如：“按照刀疤分类以后，样本是否是罪犯”的熵）

 

条件熵的表达式形式为H(Y|X)，其含义是，在X特征分类后，Y特征的熵。（其中Y特征就是最终的结果特征，如整个决策树的目的就是判断人是否是罪犯，那么这个Y特征就是“是否是罪犯”）

公式如下：

 

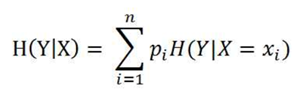
其中，pi=P(X=xi)，指的是按某特征分类的各种分类情况。

 

条件熵的推导公式如下：

 

 

信息增益

之前说了，信息增益是指分类前的信息熵（经验熵）减去分类后的信息熵（条件熵），

所以信息增益的公式为：

g(D,A)=H(D)−H(D|A)

 

信息增益的结果就是混乱度减少的量，混乱度减少的越多，分类分的越好。

 

 

决策树的生成

ID3

利用信息增益之差来生成决策树。

从树根处就开始先计算当前样本参数的经验熵，然后计算每种特征分类后的条件熵，两者取差计算出各种特征的信息增益。

选择增益最大的特征进行分类。

分类完后，继续计算当前样本的经验熵，然后计算“剩余”的特征分类的条件熵，递归此步骤。

 

使用此算法生成的树有以下缺点：

1、生成的树太“深”，容易产生过拟合。

2、分类特征变量越多，其信息增益可能越大，也越容易被选成最优特征。（如身高特征的变量可能是166cm、167cm、168cm、169cm、170cm五种变量，而性别特征只有男和女两种变量，那么身高特征分类的信息增益往往比性别特征的信息增益要大）。其实原因也很好理解，我们每次分类的目的是把样本分的更细，更“纯净”，只按男女分肯定没有按照各种身高分分的细致。

 

C4,.5

C4.5算法解决了ID3算法“偏向分支过多的特征分类，而导致过拟合”的问题。

 

所以信息增益比提出了一个“惩罚系数”，用来降低分支过多的特征的信息增益。

信息增益比公式如下：

 

其中HA(D)是以当前分类特征A作为特征变量而计算的经验熵。（之前我们的经验熵用的都是最终特征做特征变量）

 

可以看出，如果某特征分支越多，其对应的该特征经验熵也越大，相处后，信息增益比会减小。

相当于分支越多，其分支增益就会相应收到惩罚而减少某种比例。