红黑树

先贴一些二叉树的基础吧，红黑树和AVL树等这些东西不是凭空产生的，必须从二叉树开始理解和发展：

一、二叉树

不需要太多说明，仅列举一些名词和性质：

度：结点孩子个数

树的高度：根结点到叶结点的简单路径和(的最大值)

结点的深度：结点到根节点的简单路径和

树的度为所有结点度的大值，二叉树的度为2。

树的高度==叶结点最大深度，根结点深度为0，叶节点高度为0，深度也可以称作层(level)。

Ps: 有的地方会把根节点的深度设为1，叶节点高度设为1，只要能理解其实都可以，但是设置为0对代码更加友好。

二、二叉搜索树

可以看作中序遍历结果为升序数组的二叉树：即对于任意结点x，其左子树中的最大值<=x，其右子树的最小值>=x。

三、满二叉树

二叉树的每一层都满足结点个数=2^k。

四、平衡二叉树

左右子树高度相差不超过1，且左右子树皆为平衡二叉树。

换个说法：树内任意一个结点其左右子树高度相差不超过1。

五、完全二叉树

平衡二叉树，且其结点位置与相同高度的满二叉树完全一致，则可称为完全二叉树。

六、AVL树(平衡二叉搜索树)

平衡二叉树+二叉搜索树，不必是完全二叉树，即叶子结点不需要像完全二叉树那样集中在左侧，叶子结点也不需要都在同一层。

实际上我们只需要对二叉搜索树的定义加一条额外的限制就可以得到AVL树：将二叉搜索树的高度限制在logn。

可以证明AVL树的一个性质就是：AVL树的最大高度为2logn+2，因此其查找的时间复杂度为O(logn)。

七、红黑树

一种特殊的近似平衡二叉树，即肯定是二叉搜索树，但并不严格平衡。

八、堆

一种完全二叉树的线性存储结构(数组)，可以认为是完全二叉树的层次遍历结果。

一般我们在代码中实现二叉树时都会使用链式存储结构，但堆这种线性存储结构可以让我们把数组看作二叉树，从而利用树的性质对数组做一些操作(例如堆排序)。

---

红黑树正文：

二叉搜索树可以通过中序遍历快速输出有序数组，其查找任意值的平均时间复杂度为O(logn)，但是二叉搜索树在最差情况下树的高度会等于key的个数，因此有时我们需要一种更加均衡的二叉树来使查找时间复杂度更接近O(logn)，红黑树即是众多”平衡“搜索树中的一种了，它确保没有任何一条路径会比其他路径长出2倍(注意：这是维护红黑树的结果而非红黑树的定义)。

红黑树的定义(或性质)如下(首先红黑树是一颗二叉搜索树)：

1.结点有红黑两种颜色

2.根结点为黑色

3.叶结点(NIL)为黑色

4.如果结点为红，则其两个子结点皆为黑色

5.每个结点的到其后代叶结点的简单路径上，皆包含相同个数的黑色结点(我们把他称作黑高，black-height)

假设任意两个叶子节点的深度为和D1,D2，黑高为bh，结合性质2、3、4可知从根节点到叶子节点的简单路径上，黑色结点一定比红色结点多，因此有D1 >= bh > D2/2 或D2 > =dh > D1/2，因此D1*2 > D2或D2*2 > D1，即一条路径一定不可能是另一条路径的两倍长。

一般来说红黑树结构定义上比二叉搜索树多一个color属性即可：

type color bool

const (
	red, black = false, true
)

type Node struct {
	color color
	value int
	left  *Node
	right *Node
	p     *Node
}

引理1：一个有n个内部结点的红黑树，其高度至多为2log(n+1)。 证明见算法导论"红黑树"一章第一节。

注意：为简化边界条件的处理，《算法导论》一书定义红黑树时将root结点的父节点和所有叶节点统一设置为了黑色的T.nil结点，这个节点的结构和普通结点一样，区别是他的color一定是黑色的，其他属性则无所谓。

一、红黑树的旋转

准确的说这里讲的并不是红黑树的旋转，而是二叉搜索树的旋转，红黑树也是BST因此旋转代码一样(只是我们会把nil替换为T.nil)。

先来说说为什么我们要旋转红黑树？很简单，为了在删除或插入数据之后使红黑树依然保持其性质(依然是一颗红黑树)，更广义的说法是：为了使树在增删数据之后其高度依然保持"平衡"从而使其查找效率不至于下降。

我们将旋转看作使用扳手拧螺丝的行为，手握扳手处看作撬点，螺丝部位看作孩子结点，扳手本身为轴，旋转函数本身包含两个参数：二叉树本身和要旋转的结点。

定义“旋转”这个行为是以结点到孩子的路径为轴、以结点本身为撬点进行的旋转，因此旋转只有两种：即结点包含左孩子时可以右旋，包含右孩子时可以左旋。

以下述树性结构为例，左旋X时我们以X=>R路径为轴，以X为撬点，让X下降到R的左孩子，同时将R原本的左孩子变为X的右孩子，再将R与P链接即可：

	P		  	P		
	|       	|
	X       	R
   / \         / \
  L	  R       X	  Rr(R的右孩子不变)
     / \     / \
     Rl Rr  L   Rl(R的左孩子变为X的右孩子:因为Rl必定大于X且小于R符合BST的定义，且X原本的右孩子R上浮了腾出了位置)
// 这样旋转之后整棵树依然是BST，但是P的这个子树(左子树还是右子树不重要)深度发生了变化，左旋之后左子树高度+1，右子树高度-1，右旋则相反。
	P		  	P		
	|       	|
	X       	L
   / \         / \
  L	  R       Ll  X
 / \		 	 / \
Ll  Lr		    Lr  R
// 右旋与左旋类似，我们将X以X=>L的路径为轴向右侧下沉，X变为了L的右孩子，L原本的右孩子Lr成为X的左孩子，依然符合BST的定义。

据此我们来写一下右旋的伪代码(左旋的伪代码就不写了，因为算法导论里在正文给出了，右旋则是练习题)：

RIGHT-ROTATE(T, X) {
    // X has left, so we can do right rotate
	L = X.left  
    // let Lr to be X's left child
    X.left = L.right
    if L.right != T.nil {
    	L.right.p = X
    }
    // link L and P: 这一逻辑要早于让X替换Lr，因为X.p是唯一能找到P的方式，如果让21-22行代码在前，那么X.p就永久丢失了。
    L.p = X.p
    if X.p == T.nil {
    	T.root = L
    } 
    else if X == X.p.left {
    	X.p.left = L
    }
    else {
    	X.p.right = L
    // let X replace Lr
    L.right = X
    X.p = L
}

二、红黑树的插入

红黑树的插入涉及树的染色和旋转，插入部分的代码和普通二叉搜索树的插入基本一样，只需要额外三个操作：

1.为插入的叶子结点设置默认的T.nil黑色子节点

2.为新插入的代码染色

3.对树做再平衡

设置T.nil结点和染色很简单，三行简单赋值代码足矣，但之后的再平衡就比较麻烦了，因为不仅仅是简单的左旋和右旋，期间还涉及到结点颜色的变化。

我们把再平衡函数定义为RB-INSERT-FIXUP(T, X)，假设这里的X就是插入的结点。

首先插入的结点要染为红色，因为黑色会直接导致新结点所在子树的黑高发生变化，连锁反应过于巨大不利于后继代码编写(虽然染红处理也麻烦就是了)。

我们把新插入结点的父节点标记为P(arent)，爷爷标记为G(randpa)，叔叔标记为U(ncle)，虚线表示可能存在的子节点或父节点。

此外为了描述更加清晰，我这里把红黑树的T.nil叶子结点称作伪叶子结点，把伪叶子结点的父节点称作叶子结点(后文依此例)。

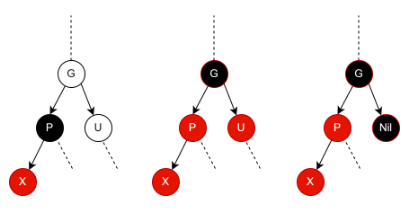
上图演示的是插入X为P的左孩子且P本身是左孩子时原红黑树的着色情况(除非特别标明否则省略T.nil)：

1.当P为黑色时，根据红黑树的定义增加一个Red X不可能影响任意结点的黑高，因此我们不需要任何操作，也无需关心G和U的颜色，树还是一颗红黑树。

2.当P为红色时，其父节点G必然为黑色(据性质4)，插入X之前G->P->P的左孩子(T.nil)这条路径的黑高为2，因此P的右孩子一定是T.nil，U则一定是T.nil或红色的叶子结点。

    2.1) 当U是红色时，我们只需要把G/P/U的颜色统一反转即可，这样黑高未变化，P和U也满足性质4；但是G变为了红色可能违反性质4，那么我们看下能否针对G进行递归以便实现红黑树性质维护，这点之后再来验证。

    2.2) 当U是黑色伪叶子节点时，无法通过简单的颜色转换满足性质4，此时我们考虑对G进行右旋：

        2.2.1）右旋G之后G变为P的右孩子，且G本身成为叶子结点，此时只要把G和P的颜色互换即可，这样性质4和性质5都未违反。

        2.2.2）假设X是P的右孩子呢？<型结构的子树显然不能通过一次旋转就平衡，我们可以先把P左旋，然后再按2.2.1的逻辑把G右旋并换色G/X即可。注意到这个逻辑显然通过递归即可实现，因为左旋P之后下次递归时的条件和2.2.1一模一样，因此会直接访问2.2.1分支，但直接完成两次旋转也是可行的(先左旋P再右旋G)。

3.此外当P是G的右孩子时，我们只要把左右互换一下即可，没什么可说的。

我们先把当前的思路整理为伪代码(相比书上的示例，我这里的伪代码用了递归，更好理解一些)，最后再去解决那个遗留的最大问题：能否针对G进行递归以便实现红黑树性质维护？

RB-INSERT-FIXUP(T, X) {
    P, G = X.p, X.p.p
	// 实现上述场景1
	if P.color == BLACK {
		T.root.color = BLACK	// 处理插入的是root结点的场景
		return
	}
	// 实现上述场景2
	if P == G.left {    
		U = G.right   
		// 实现上述场景2.1
		if U.color == RED {   
			P.color, U.color, G.color  = BLACK, BLACK, RED
			// 遗留问题: 待验证
			RB-INSERT-FIXUP(T, G)   
			}
		// 实现上述场景2.2
		else
			{
			// 实现上述场景2.2.1
			if X == P.left { 
				P.color, G.color = BLACK, RED
				RIGHT-ROTATE(T, G)   
				}
			// 实现上述场景2.2.2
			else {
				LEFT-ROTATE(T, P)
				RB-INSERT-FIXUP(T, P)   
				}
		}
    // 实现上述场景3
	else 
		{
		// 反转上述代码中的左、右即可
		}
    T.root.color = BLACK	// 最后把根节点设为黑，此操作不会违反红黑树的任意一条定义
}

OK，那么现在我们只需要验证下第15行代码是否正确即可：

我们把G当作了新的X传入了RB-INSERT-FIXUP()，新的X不再是一个结点而是一棵树(看作一颗根节点为红色的红黑树)，根据红黑树的定义3-6行的场景1肯定能跑通，场景2.1不涉及X子树的性质变更因此也没问题，场景2.2中右旋G时进行了颜色变换，通过简单计算就能知道P的右子树和G的左子树黑高都未变化，而左旋P时从下图可以看出，P和X的黑高是一样的(都是红结点)，所以左旋P对G/P/X三棵子树的黑高都不构成影响。

 

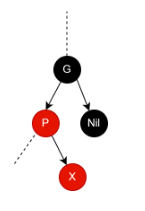
至此我们可以正常上述伪代码是可行的。

从上述代码还可知，插入一个新结点时，红黑树至多旋转两次，因为分支1和分支2.1都不涉及旋转，只涉及颜色转换，而分支2.2一旦执行函数就会终止了，分支2.2两个子分支中旋转次数至多为2。

三、红黑树的删除

红黑树的删除要比插入更复杂一些，基本思路和RB-INSERT相似，都是复用TREE-DELETE的代码，然后添加RB-DELETE-FIXUP来修复红黑树性质，但是RB-DELETE-FIXUP理解起来要比RB-INSERT-FIXUP更难(伪代码本身不难，难的是证明伪代码是正确的)。

四、红黑树的优劣

相比于AVL树，红黑树不需要严格平衡，因此其写入效率要比AVL树更好一些，增删数据时旋转起来比AVL树简单太多了。而相比于B树和B+树这种基于磁盘的数据结构，红黑树更适合能完全存储于内存中的数据，因为B树的构造是着重考虑了磁盘IO的。

五、其他

红黑树在面试时很少会让你写出他的插入或删除代码，因为实在是有些麻烦(当然相比AVL树还是简单些)。我在知乎某个答案里看到过据说算法导论的作者考虑把红黑树一章替换为跳表，跳表这种结合了链表和顺序表长处的数据结构实现起来更简单，效率却不相上下。