咕咕咕

颓废了太久了也太久没有做 🕊 了

找点事情做防止自己过于颓废。

尽量写题解

题目 完成情况 题目 完成情况 题目 完成情况
CF549E CF674G QAQ ARC103_F QAQ
CF594E AGC034_F QAQ AGC030_D QAQ
CF575E AGC035_C QAQ AGC026_F QAQ
CF607E AGC038_E QAQ AGC030_C QAQ
CF611G AGC034_D QAQ AGC024_F
CF571E CF696F ARC093_E
CF573E CF704E ARC103_D QAQ
CF627F AGC035_D QAQ AGC033_F
CF538G CF674D ARC101_F
CF566C CF700E QAQ ARC092_F
CF566E AGC034_E QAQ AGC022_D
CF613E AGC033_E AGC021_F
CF528C AGC038_F AGC029_E
CF611H AGC036_D AGC027_E
CF626G CF666D ARC102_F
CF605E AGC031_E QAQ AGC028_D
CF536D AGC027_F AGC024_E
CF553E AGC037_F AGC029_C
CF571D CF708E ARC093_F
CF603E AGC036_E AGC021_E
CF590E AGC031_D QAQ AGC026_E
CF587F CF685C ARC096_E
CF587D CF674F ARC091_F
CF575I AGC035_F AGC028_F
CF504E CF671E ARC101_E QAQ
CF585F CF708D ARC095_F
CF521D AGC036_F AGC028_C
CF585E AGC032_C AGC023_F QAQ
CF568C CF666E AGC025_E
CF568E CF704C ARC100_F
CF538H AGC032_D AGC024_D
CF582E AGC039_E AGC025_F QAQ
CF526F AGC037_D AGC020_E
CF521E AGC030_F QAQ AGC026_D
CF526G CF698D ARC089_F
CF582D CF634F AGC020_D
CF578F CF704B ARC099_F
CF578E AGC035_E AGC025_D QAQ
CF516E AGC030_E QAQ AGC027_D
CF576E CF704D ARC096_F
CF547E CF671D ARC097_F
CF547D AGC033_D AGC031_F
CF575A CF639E AGC039_F
CF559E AGC037_E AGC020_F
CF512D AGC028_E AGC022_F QAQ
CF506E CF639F AGC039_D QAQ
CF576D AGC029_F AGC022_E QAQ
CF555E AGC032_E AGC023_D QAQ
CF506C CF679E ARC098_F
CF516D AGC032_F AGC023_E QAQ

CF674G

众所周知求序列出现次数超过一半的众数有一个辅助空间 \(O(1)\) 复杂度 \(O(n)\) 的做法。

然后很显然这个做法是可以扩展的，做法类似：碰到一个有的数则把那个数的计数 \(+1\)，否则全体 \(-1\)。正确性我不会证然后感觉上挺对的？

那么这个区间推平还有询问很自然地把它放到线段树上，合并的时候暴力合并，把一边的数都并到另一边。（其实并的顺序没什么关系）

Code

AGC039_D

平面几何神仙题。看了半个小时无从下手一看完题解就喙了 QAQ

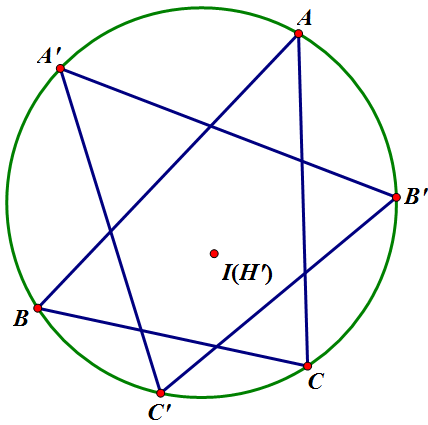
如图，\(△ABC\) 内接于圆，内心为 \(I\)，延长 \(AI\)，\(BI\)，\(CI\) 交圆于 \(A'\)，\(B'\)，\(C'\)，下面证明：\(I\) 是 \(△A'B'C'\) 的垂心。

事实上，由鸡爪定理知，\(A'A = A'I\)，\(B'A = B'I\)，故 \(A'B' \bot AI\)，即 \(C'I \bot A'B'\)。同理，\(A'I \bot B'C'\)，\(B'I \bot A'C'\)，故 \(I\) 是 \(△A'B'C'\) 的垂心。注意到 \(A'\)，\(B'\)，\(C'\) 分别是 \(\overset{\frown}{BC}\)，\(\overset{\frown}{CA}\)，\(\overset{\frown}{AB}\) 的中点（不经过 \(A\)，\(B\)，\(C\)），坐标容易计算。

又由欧拉线定理，\(△ABC\) 的外心 \(O\)，垂心 \(H\)，重心 \(G\) 三点共线，且 \(\vec {OH} = 3 \vec {OG} = \vec {OA} + \vec {OB} + \vec{OC}\)。注意到这里的三角形外心都是原点，故 \(H = A + B + C\)。

考虑计算两个点 \(A\)，\(B\) 造成的贡献。若 \(C\) 在优弧 \(AB\) 上，则 \(C'\) 在劣弧 \(AB\) 上；反之，若 \(C\) 在劣弧 \(AB\) 上，则 \(C'\) 在优弧 \(AB\) 上。

这样的话只要 \(O(n ^ 2)\) 枚举两个点计算贡献就好了 QAQ

Code

CF700E

上古时期用后缀数组写过一发，这次换 SAM。

话说 SAM 真的比后缀数组好想很多的说

在 parent 树上 dp，每个点 \(u\) 找到离它最近的在它里面出现两次的祖先 \(v\)，即 \(v\) 的 \(endpos\) 集合在 \([pos_u - len_u + len_v, pos_u]\) 中出现两次，注意到 \(v\) 是 \(u\) 的严格后缀，所以只要检查 \(v\) 的 \(endpos\) 集合在 \([pos_u - len_u + len_v, pos_u - 1]\) 中是否出现，可以使用线段树合并实现。

实现的时候对于一段 dp 值相同的链记录顶端会好写一点 QAQ

Code

AGC030_C

首先考虑 \(n\) 的大小不限怎么做。有一个很 \(naive\) 的想法就是第 \(i\) 行填 \(i\)，但是似乎没法扩展。考虑按照斜线填数。

然后考虑 \(n \leq 500\)。注意到可以把每一条斜线交替填数，显然满足要求，然后就做完了。

Code

AGC030_D

首先把方案数转化为概率，最后乘上 \(2 ^ Q\) 即可。

记 \(P_{i, j}\) 为 \(a_i > a_j\) 的概率，设欲交换的位置为 \(x, y\)。

考虑一种情况，对于 \(i \neq x\) 且 \(i \neq y\) 则有 \(\frac 12\) 的概率 \(P_{i, x}\) 不变（即 \(x, y\) 不交换），有 \(\frac 12\) 的概率 \(P_{i, x} \leftarrow P_{i, y}\)（即 \(x, y\) 交换），故 \(P_{i, x} \leftarrow \frac 12(P_{i, x} + P_{i, y})\)。其余情况同理可求。

注意到一次交换只会对 \(i = x\) 或 \(i = y\) 或 \(j = x\) 或 \(j = y\) 的 \(\operatorname {O} (n)\) 个位置的值造成贡献，复杂度为 \(\operatorname {O} (n^2 + nQ)\)。

Code

AGC030_E

挺有意思的一道题。

记序列为 \(s\)。对于一个中间的位置 \(i\)，其可操作的一个必要条件是 \(s_{i - 1} \neq s_{i + 1}\)。

注意到一次操作（\(001 \rightarrow 011, 011 \rightarrow 001, 100 \rightarrow 110, 110 \rightarrow 100\)），不会改变 \(0\) 和 \(1\) 之间的相对位置关系，考虑在分界线染色。特殊地， \(01\) 为黑，\(10\) 为白。原来的问题就转化为了：最少移动多少步，使得两个序列的分界线重合，过程中相邻两个分界线距离为 \(1\) 或 \(2\)。

不过这样似乎不是很好处理两边的情况，考虑在左右两边搞一个无穷的 \(01\) 交替的序列，这样就可以让中间的分界线和两边的互相转化了。特别地，两边的分界不受距离限制。

最后考虑一个问题：如果已经知道哪些分界线要对齐，最少需要移动多少步。可以发现答案的下界是对应分界的距离和，感性理解一下这似乎就是答案。（我不会证）

注意到可能的对齐情况有 \(\operatorname {O} (n)\) 种，每次计算复杂度 \(\operatorname {O} (n)\)，总时间复杂度 \(\operatorname {O}(n^2)\)。

Code

AGC030_F

个人感觉比 E 题简单一点。

首先把 \(A_{2i - 1} \neq -1\) 且 \(A_{2i} \neq -1\) 的扔掉。剩下的要么两个都不确定，要么有一个确定。

考虑把 \(1～2N\) 排成一列，在配对的之间连边。

注意到若配对的一端的位置已经确定，则另一端的位置也必定确定。否则，注意到在不确定的位置配对的对数是一定的，记为 \(C\)，可以先不考虑顺序，最后把答案乘上 \(C!\)。

然后就很自然有一个 dp 做法。

考虑数字从大到小 dp。记 \(dp_{i, j, k}\) 为当前考虑完 \(\geq i\) 的数，剩下 \(j\) 个位置确定的未匹配，\(k\) 个位置不确定的未匹配的方案数。则答案就是 \(dp_{1, 0, 0}\)。然后分类讨论一下：

  • 若当前点位置确定
    • 与后面一个位置不确定的点匹配。
    • 留着等以后被匹配。
  • 若当前点位置不确定
    • 与后面一个位置不确定的点匹配，这里不用乘系数，之前已经考虑过了。
    • 与后面一个位置确定的点匹配，注意这里转移要乘上一个 \(k\)，因为可以和后面任意一个已确定的匹配。
    • 留着等以后被匹配。

Code

AGC034_E

在小公主的指导下完成了此题。

硬点最后到了哪个点上，考虑 dp。记 \(dp_{u, x}\) 表示当前考虑 \(u\) 的子树，当前考虑的所有棋子到 \(u\) 的距离和为 \(x\) 是否可行，然后就有一个十分 naive 的会 T 的做法了！

发现可行的 \(x\) 是一段区间中奇偶相同的所有数，于是只要维护可行的最大值和最小值就可以了。

至于是否可行，只要看一下最后 \(min_{rt}\) 是否等于零就可以了。

时间复杂度 \(\operatorname O (n^2)\)

Code

AGC026_F

按照 \(n\) 的长度奇偶分类的方法好妙啊！

令先、后手分别为 \(A, B\)。

  • 若 \(n\) 为偶数，\(A\) 从端点开始一定不劣。因为如果从中间开始，会被 \(B\) 获得先手，\(A\) 可取得的价值一定不优。
  • 若 \(n\) 为奇数。
    • 如果 \(A\) 取奇数位置，答案和从端点开始相同。
    • 如果 \(A\) 取偶数位置，就把原问题分成两个长度为奇数的子问题，其中一边全取下标奇数的位置，另一边继续递归。则问题转化为了：\(A\) 可以钦定划分点，\(B\) 可以选择一段下标为奇数的和剩下的段下标为偶数的位置使得和尽量小。可以先钦定 \(A\) 取了所有下标为偶数的值，然后使最小的一段中的奇数下标减偶数下标的值尽量大，这个显然可以通过二分解决。但是这样的 check 似乎是 \(n^2\) 的，考虑记录所有可行划分点的前缀最小值，就可以 \(\operatorname O(n)\) 愉快 check 了！

Code

AGC035_C

显然对于 \(2\) 的幂次是无解的。

注意到有 \(2k\bigoplus 2k + 1 = 1\)，然后就可以两个数一组和 \(1\) 连，大概就是类似于 \(1\longleftrightarrow 2k, 1\longleftrightarrow 2k+1,2k\longleftrightarrow n+2k+1,2k+1\longleftrightarrow n+2k\)。

对于 \(n\) 为偶数的情况，最后多出来的那个数可以找到一组 \((x, y)\) 满足 \(x\bigoplus y\bigoplus 1=n\)，连就完事了。

Code

AGC034_F

设 \(f_S\) 表示到 \(S\) 状态的步数，则 \(\forall S > 0,f_S = 1 +\sum_{j\bigoplus k=S}f_jp_k\)。

记 \(f\) 的集合幂级数为 \(F\)，\(p\) 的集合幂级数为 \(P\)，则有：

\[F + c = I + F\bigoplus P\tag{1} \]

即

\[\operatorname{FWT}(F)+\operatorname{FWT}(c)=\operatorname{FWT}(I)+\operatorname{FWT}(F)\times\operatorname{FWT}(P) \]

注意到 \(\operatorname{FWT}(P)_0 = 1\),故 \(c=\operatorname{FWT}(I)_0 = 2^n\)。

显然有 \(F\bigoplus 1=F\)，在 \((1)\) 式两边同时减去 \(F\)，有：

\[2^n = I + F\bigoplus(P - 1) \]

也即

\[\operatorname{FWT}(2^n - I) = \operatorname{FWT}(F)\times\operatorname{FWT}(P - 1) \]

显然，\(\forall S>0,\operatorname{FWT}(2^n - I)_S\neq 0,\operatorname{FWT}(P-1)\neq 0\)，可以轻易求出 \(\operatorname{FWT}F_S(S>0)\)。

对于 \(S=0\)，可以使用待定系数，开始钦定一个 \(f_0\) 最后减掉即可。

Code

AGC031_E

发现这个数据范围不对，考虑费用流（雾

发现这个数据范围小的离谱，甚至可以承受跑 \(n\) 次费用流那什么都不管跑它 n 次再说

先考虑一维的情况，枚举选的珠宝数量 \(k\),则横坐标小于等于 \(a_i\) 的最多 \(b_i\) 这个限制等价于最后 \(k - b_i\) 个横坐标必须大于 \(a_i\)，大于等于类似考虑。这样可以搞出每一个点的可行坐标范围，很容易可以转化为费用流模型，采用最大费用最大流即可，最后检查一下是否流满更新答案即可。

转到二维，与一维情况类似，两边各弄这样的 \(k\) 个点即可。

Code

AGC031_D

设 \(A = qp^{-1}q^{-1}p\)，则有 \(a_{n+6}=Aa_nA^{-1}\)在纸上手模 15 项可得

发现这个结论以后应该容易证明，\(a_n=a_{n-1}a_{n-2}^{-1}=Aa_{n-7}A^{-1}Aa_{n-8}^{-1}A^{-1}=Aa_{n-6}A^{-1}\)

然后快速幂即可。

Code

AGC038_E

记 \(S=\sum A\)，\(T = \sum B\)。设 \(F_k(x)\) 表示第 \(i\) 个加数器加了不少于 \(B_k\) 次的概率指数生成函数，则

\[\begin {align*} F_k(x) & = \sum_{i = B_k}\left(\frac{A_k}{S}\right)^i\frac{x^i}{i!} \\ & = e^{\frac{A_k}{S}x} - \sum_{i = 0}^{B_k - 1}\left(\frac{A_k}{S}\right)^i\frac{x^i}{i!} \end {align*} \]

则答案为：

\[\sum_{i = 0}^{+\infty}\left(1 - i![x^i]\prod F_k(x)\right) \]

对于后面的 \(\prod F_k(x)\)，注意到它应该有这样的形式：

\[\prod F_k(x) = \sum_{i = 0}^S e^{\frac iSx}P_i(x) \]

其中 \(P_i(x)\) 是次数不超过 \(T\) 次的多项式，且 \(P_i(x)\) 可以通过 \(\operatorname O(ST^2)\) 大力 dp 得出。记 \(P_{i, j} = [x^j]P_i(x)\)，则答案为：

\[\begin {align*} & \sum_{i = 0}^{+\infty}\left(1 - i![x^i]\prod F_k(x)\right) \\ = & -\sum_{i = 0}^{+\infty}i![x^i]\sum_{k=0}^{S-1}e^{\frac kSx}P_k(x) \\ = & -\sum_{i = 0}^{+\infty}i!\sum_{k=0}^{S-1}e^{\frac kSx}\sum_{j = 0}^T P_{k, j}\frac {\left(\frac kS\right)^{i-j}}{(i - j)!} \\ = & -\sum_{k = 0}^{S - 1}\sum_{j = 0}^TP_{k, j}\left(\frac kS\right)^{-j}\sum_{i = 0}^{+\infty}\left(\frac kS\right)^i\frac{i!}{(i-j)!} \\ = & -\sum_{k = 0}^{S - 1}\sum_{j = 0}^TP_{k, j}\left(\frac kS\right)^{-j}j!\sum_{i = 0}^{+\infty}\left(\frac kS\right)^i\binom ij \\ \end {align*} \]

考虑最后面那坨东西。记 \(F_j(x)=\sum_{i = 0}^{+\infty}x^i\binom ij\)，则 \(F_0(x)=\frac 1{1-x}\)，且对于 \(j > 0\)，有：

\[\begin {align*} F_j(x) & = \sum_{i = 0}^{+\infty}x^i\binom ij \\ & = \sum_{i = 0}^{+\infty}x^i\left(\binom{i-1}{j}+\binom{i-1}{j-1}\right) \\ & = xF_j(x)+xF_{j-1}(x) \end {align*} \]

故 \(F_j(x) = \frac x{1-x}F_{j-1}(x) = \frac {x^j}{(1-x)^j}\)，递推即可。

Code

AGC034_D

曼哈顿距离可以写成 \(|x_1-x_2|+|y_1-y_2|=\max\{(x_1+y_1)+(-x_2-y_2),(x_1-y_1)+(-x_2+y_2),(-x_1+y_1)+(x_2-y_2),(-x_1-y_1)+(x_2+y_2)\}\)，建四个虚拟点分别表示这四种情况（注意对应），跑最大费用最大流即可

Code

AGC035_D

显然 \(A_1\) 和 \(A_n\) 没有什么用处，最后加到答案里就好了。

考虑倒着做，假设最后一个删的位置是 \(i\)。那么对于 \(i\) 左边的数，有一部分贡献到了 \(i\) 上，有一部分贡献到了最左边的虚空。对于贡献到虚空的，显然贡献了 \(1\) 次；对于贡献到 \(i\) 的，在删掉 \(i\) 的时候还会向虚空贡献 \(1\) 次，共贡献了 \(2\) 次。对于 \(i\) 右边的情况同理。

于是很自然地有一个 dp：\(dp_{L,R,pl,pr}\) 表示当前考虑区间 \([L,R]\)（不包括端点），向左贡献的倍数为 \(pl\)，向右贡献的倍数为 \(pr\) 的最小值。枚举当前区间最后删去的数 \(i\)，显然有转移:

\[dp(L,R,pl,pr)=\min_{i=L+1}^{R-1}\left(dp(L,i,pl,pl+pr)+dp(i,R,pl+pr,pr)+a_i*(pl+pr)\right) \]

显然状态数上界是 \(\operatorname{O}(n^22^n)\) 的。SV 通过我不会的精细分析得出是 \(\operatorname{O}(2^n)\) 的。反正能过管这么多干嘛

Code

AGC022_F

神仙 dp 题。

每个数对答案的贡献一定是 \((-1)^c2^dx^i\) 的形式。发现 \(x\) 很大，故每个数可以分开来算贡献。

考虑若将 \(A\) 关于 \(B\) 作了一次对称，则将 \(A\) 设为 \(B\) 的父亲。这样每个点的 \(d\) 显然只与它的深度有关，容易处理，而 \(c\) 则与它儿子个数的奇偶性和它到祖先的链上在它之后被选点数的奇偶性相关。

推到这一步发现自己不会了偷偷瞄一眼题解

考虑每个点和他父亲的符号是否相同，那么影响这个的因素仅有它儿子数的奇偶性和在它之前指向它的父亲的点数的奇偶性。

考虑按深度转移。设 \(dp_{i,j}\) 表示当前共有 \(i\) 个点，上一层有 \(j\) 个儿子数为奇数的点数，枚举这一层的点数和与父亲符号不同的点数，可以得到这一层儿子数为奇数的点数。转移时乘上一个组合数即可。

Code

AGC025_D

与一个点距离平方为 \(D(D\leq 2\times 300^2)\) 的点最多 \(96\) 个，所以直接建二分图跑最大匹配是可以的。

但是我不想写这个东西怎么办 w但是其实 \(n^2\) 这个界蛮松的，考虑这样一种染色方式：

  • 若 \(D\bmod 4=1\)，说明 \(\Delta x\) 和 \(\Delta y\) 一奇一偶，考虑棋盘形染色。
  • 若 \(D\bmod 4=2\)，说明 \(\Delta x\) 和 \(\Delta y\) 同为奇数，隔行/隔列染色即可。
  • 若 \(D\bmod 4=0\)，说明 \(\Delta x\) 和 \(\Delta y\) 同为偶数，考虑将 \(D\) 不断 \(\div 4\) 转化为上面两个问题。
  • 若 \(D\bmod 4=3\)，\(\tan \frac{\pi}2\)

这样根据 \(D1\) 和 \(D2\) 染完色以后一定有至少 \(n\) 个未被染色的地方（考虑鸽子巢原理）。

Code

ARC101_E

考虑容斥。记 \(f_S\) 表示 \(S\) 中的边全部未被覆盖的方案，则 \(ans=\sum_S(-1)^{|S|}f_S\)。

若一个连通块 \(T\) 的价值为 \([2|n]\frac{n!}{2^{\frac n2}\left(\frac n2\right)!}\)，则 \(f_S\) 等于它分割出的所有连通块的价值的乘积。

考虑树形 dp。记 \(dp_{u,i}\) 表示以 \(u\) 为根的子树中，与 \(u\) 相连的连通块的大小为 \(i\) 的方案数。特殊地，\(dp_{u,0}\) 表示 \(u\) 和父亲断开，转移类似树上背包。注意 \(u\) 和父亲断开时 \(|S|\) 增大了 \(1\)，要乘上一个系数 \(-1\)。

QAQ

AGC022_E

手建毕克自动机。因为开始的状态是不确定的，所以从 1 和 11 状态开始倒推。

Code

AGC025_F

看到这个题想起了那个均摊 \(\operatorname O(n)\) 的二进制加数器。于是大胆猜测这个题也是均摊的

首先容易发现，会自发产生进位只有可能某一位为 1 1，并且如果没有阻碍的话会每一轮前进一格。当遇到 0 1 或 1 0 时停止，并由 0 1 或 1 0 继续向前产生进位。考虑从高位到低位模拟这个过程，把所有 0 1 和 1 0 存入一个栈中，每次遇到 1 1 向前模拟进位即可。

懒得写势能函数注意到 1 1 每向前走两步至少弹栈一次，所以复杂度是 \(\operatorname O(n)\)。

Code

AGC023_D

神仙题。

先来考虑一些比较简单的情况。

  • 所有人在起点同一侧，那么车一定是往那一侧开到底。
  • 最后只剩下两个位置有人，那么车一定是先往人多的一侧开再往人少的一侧开（人数相同向左开）。

对于上面的第二种情况，假设人少的一侧位置为 \(x\)，回家时间为 \(t\)；人多的一侧位置为 \(y\)，回家时间为 \(T\)。则一定有 \(t=T+|x-y|\)，显然 \(T\) 仅与 \(t\) 有关。也就是说，在此之前，\(x\) 的人会希望 \(y\) 的人先回到家，以使自己早回到家。因此倒着做，每次把两边人少的一边向人多的一边合并即可。

Code

AGC023_E

设 \(cnt_i\) 表示限制大于等于 \(i\) 的个数，考虑从小到大填数，易知总方案数 \(sum = \prod_{i=1}^n\left(cnt_i - (n - i)\right)\)。

先考虑枚举两个位置 \(i<j\)，计算它们的贡献。

  • \(A_i = A_j\)，显然贡献为 \(\frac 12sum\)。
  • \(A_i < A_j\)，当 \(P_j > P_i\) 时一定不会对答案产生贡献，所以可以强制 \(A_j = A_i\)，然后按上面的方法做就可以了。
  • \(A_i > A_j\)，好像不能直接套用上面的方法，考虑令 \(A_i = A_j\)，用总数减去不产生贡献的数量，然后做法类似上面。

这样可以做到 \(O(n^2)\)。

考虑强制 \(A_j = A_i\) 的时候发生了什么，容易发现实际上是改变了连续一段 \(i\) 的 \(cnt\) 值。然后就可以考虑以 \(A_i\) 为下标维护一个前缀积的和就好了。

Code

AGC023_F

树上贪心，以 \(\frac{cnt_0}{cnt_1}\) 为关键字，不断合并上去就可以了。

Code

posted @ 2020-02-13 21:35  realSpongeBob  阅读(581)  评论(0)  编辑  收藏  举报