一个最大张角尺规可作性命题的分析与证明

引言：

前一阵前同事小罗和我交流他孩子考试的一道初三数学题，说第三问全年级全军覆没。这道题是这样的：

在平面直角坐标系 xOy 中，已知抛物线 y = x² - 2ax - 3a²（其中 a > 0）与 x 轴交于 A，B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C，顶点为 D，OC = 3OA.

(1) 求 a 的值；
(2) 点 M(m, n) 与点 N(n, m) 是抛物线上两个不重合的点，求 m - n 的值；
(3) 点 P 是抛物线对称轴上一点，在直线 BC 上有且仅有一个点 Q，使得 ∠AQP = 45°，求点 P 的坐标.

在完成了该题第三问的解答后，很自然就引出了如下的一个命题。

命题：在平面直角坐标系中，从 x 轴的上方任意取定不同两点 M 和 N. 则通过尺规作图一定可以找出 x 轴上的一点 Q，使得 MQN 张角最大.

分析与证明：先证明最大张角点的存在性.

第一步：若最大张角点存在，考察其满足什么性质.

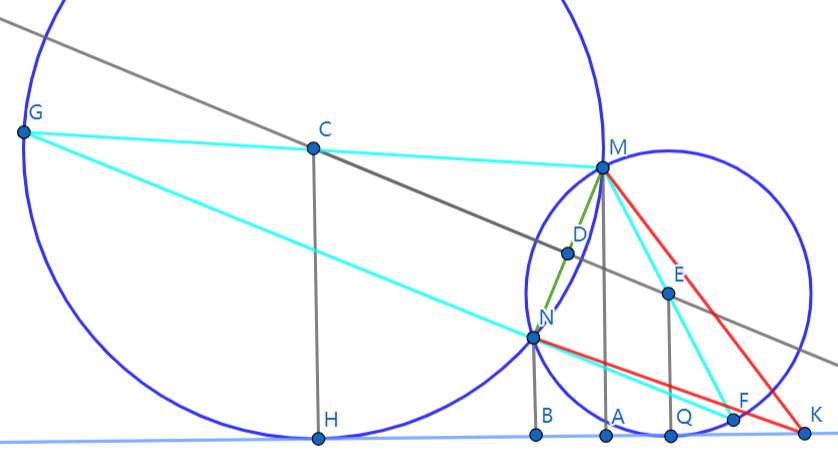
如上图所示，直线 AB 为 x 轴，M 和 N 是 x 轴上方不同两点. 记 M 和 N 到 x 轴的距离分别为 2a 和 2b，即 MA = 2a，NB = 2b，并记 AB = 2c，其中：

①           a > 0, b > 0, c ≥ 0 且 c = 0 时，a ≠ b.

易知满足条件 ① 的一组 a, b, c 唯一确定了 x 轴上方不重合两点 M 和 N 的一种相对位置，即确定了两点的高度以及它们的水平距离（线段 MN 沿水平方向作平移变换或沿某条垂直 x 轴的直线作轴对称变换均视作保持相对位置不变 ）；反之，x 轴上方不重合两点 M 和 N 的任何一种相对位置都对应有唯一的一组 a, b, c.

上图示例是 a > b 的情形.

D 是 MN 的中点，CD 是 MN 的垂直平分线. 过点 M 和 N 且与 x 轴相切的圆的圆心显然一定落在直线 CD 上. 上图的情形这样的圆有两个：一个以点 C 为圆心，与 x 轴的切点为 H；另一个以点 E 为圆心，与 x 轴的切点为 Q.

在 x 轴上任取一点 K，因为有两个过 M 和 N 且与 x 轴相切的圆，无论 K 取在点 H 的左侧，或是点 Q 的右侧，又或是线段 HQ 上，线段 MK 和 NK 必定有一条会穿过其中一个圆的内部，继而由圆周角的性质可知：

②          ∠MKN ≤ max {∠MHN, ∠MQN}.

上图中，MG 和 MF 分别是两个圆的直径，即有 GN ⊥ MN，FN ⊥ MN，于是 G、N、F 三点共线，MGF 构成一个三角形，由大边对大角可知：

③         ∠MHN = ∠MGN < ∠MFN = ∠MQN.

综合 ② 和 ③，即有 ∠MKN ≤ ∠MQN.

由上述分析，容易猜想到最大张角点就是过点 M 和 N 且与 x 轴相切的所有圆中半径最小的那个圆与 x 轴相交的切点.

第二步：考察一般情形下，过点 M 和 N 且与 x 轴相切的圆是否一定存在以及存在多少个这样的圆的问题.

所谓一般情形，就是满足条件 ① 的情形. 在上图中，令点 B 为平面直角坐标系的原点，则 点 N 的坐标为 (0, 2b)，点 M 的坐标为 (2c, 2a)，点 D 的坐标为 (c, a+b).

直线 MN 的斜率为 k = (a-b)/c，于是 直线 CD 的方程为 y - (a+b) = (x - c)·c/(b-a)，即

④       cx + (a-b)y = a² - b² + c².

容易验证，当 c = 0 或 a = b 时，直线 CD 的方程同样满足 ④.

先讨论 c = 0 的情形. 此时 MN 所在直线垂直于 x 轴，MN 的垂直平分线与 x 轴平行. 此时符合要求的圆有两个，半径都等于 MN 的中点 D 到 x 轴的距离.  如下图所示： 

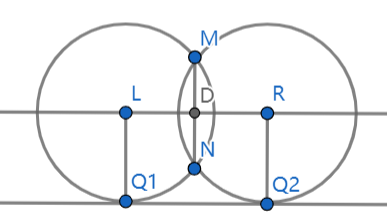
在 x 轴上任取一点 K，无论 K 取在点 Q₁ 的左侧，或是点 Q₂ 的右侧，又或是线段 Q₁Q₂ 上，线段 MK 必定会穿过其中一个圆的内部. 因此，有圆周角的性质可知，两个圆与 x 轴的切点都是最大张角点. 

以下讨论 c ≠ 0 的情形. 设点 P 是直线 CD 在 x 轴上方部分的一个动点，其坐标记为 (p, r)，其中 r > 0 是点 P 到 x 轴的距离. 

PM² = DM² + PD² =  (2c - c)² + (2a - a - b)² + (c - p)² + (a + b - r)²

   = c² + (a - b)² + (c - p)² + (a + b - r)²

点 P 在直线 CD 上，故由 ④ 有 cp + (a - b)r = a² - b² + c²，即有

cp - c² = c(p - c) =  a² - b² - (a - b)r = (a - b)(a + b - r). 于是

(c - p)² = [(a - b)/c]²(a + b - r)² = k²(a + b - r)². 

代入上式，得到

PM² = (k² + 1)(r - a - b)² + c² + (a - b)².

以 P 为圆心，r 为半径的圆显然与 x 轴相切，该圆过点 M 和 N 的充要条件是 PM² = r². 于是问题等价为：

判断两个二次函数 y = x² 和  y = (k² + 1)(x - a - b)² + c² + (a - b)² 在第一象限是否有交点以及有几个交点.

后者可以简记为 y = u(x - v)² + w，其中 u = k² + 1，v = a + b，w = c² + (a - b)².

当 k = (a - b) / c = 0，即 a = b（M 和 N 等高）时，由 (x - v)² + w = x² 可得 x = (v² + w) / (2v) > 0. 符合要求. 此时，符合要求的圆只有一个，如下图所示：

 

这种情形下，尽管只有一个符合要求的圆，但是在 x 轴上任取一点 K，无论 K 取在点 Q 的左侧，或是点 Q 的右侧，线段 MK 和 NK 必定有一条会穿过圆的内部，同样由圆周角的性质可知 ∠MKN ≤ ∠MQN，即点 Q 就是最大张角点.

当 k ≠ 0 时，u(x - v)² + w = x² 是一个一元二次方程，展开即为 (u - 1)x² - 2uvx + uv² + w = 0. 其判别式为：

Δ = 4u²v² - 4(u - 1)(uv² + w)

   = 4(k² + 1)²v² - 4k²(k² + 1)v² + 4k²w

   = 4k⁴v² + 8k²v² + 4v² - 4k⁴v² - 4k²v² + 4k²w

   = 4k²v² + 4v² + 4k²w > 0.

 因此，u(x - v)² + w = x² 有两个根：

⑤     x₁ = [2uv - Δ^1/2] / (k²)，x₂ = [2uv + Δ^1/2] / (k²).

显然 x₂ > 0. 而由 Δ > 0 以及 Δ = 4u²v² - 4k²(uv² + w) < 4u²v² 可知 Δ^1/2 < 2uv. 因此，x₁ > 0. 这说明：

当 k ≠ 0 时，y = x² 和  y = (k² + 1)(x - a - b)² + c² + (a - b)² 在第一象限总有两个交点. 如下图所示：

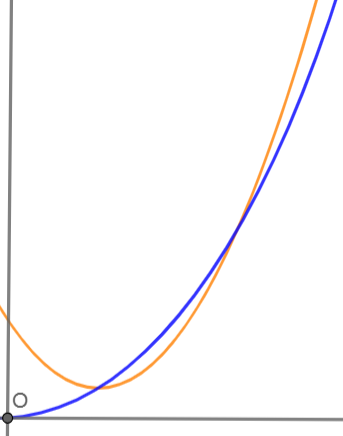
这两个交点的横坐标，即 x₁ 和 x₂，分别就是过 M 和 N 且和 x 轴相切的两个圆的半径. 以下进一步考察这两个圆相对 MN 的位置关系.

先看一种特殊情形. 过点 M 和 N 的最小的圆，其圆心必然正好是 MN 的中点 D，假如这个圆和 x 轴相切，此时圆的半径正好等于点 D 的纵坐标 a+b. 如下图所示：

那么这个圆必定是半径较小的那个圆. 这是因为让 动点 P 沿点 D 往点 L 方向移动，以 P 为圆心且与 x 轴相切的圆半径会越来越小，但这些圆都不过点 M 和 N.

由于 MN 是小圆的直径，且 c ≠ 0，点 M 和 N 必然分属该圆的左右半圆弧. 于是在 x 轴上任取一点 K，无论 K 取在点 Q 的左侧，或是点 Q 的右侧，线段 MK 和 NK 必定有一条会穿过圆的内部，同样由圆周角的性质可知 ∠MKN ≤ ∠MQN，即点 Q 就是最大张角点.

上图中红色线段 M'N' 是圆中平行 MN 的弦，位置低于 MN 且点 M' 和 N' 也分属该圆的左右半圆弧. 不难发现任取 x 轴上一点 K，都有 ∠M'KN' ≤ ∠ M'QN'. 也就是说上图中的圆也是过 M' 和 N' 且与 x 轴相切的两个圆中较小的那一个.

但当 MN 继续平行下移到上图中绿线所示的 M''N''，此时 M'' 和 N'' 都处在该圆的右半圆弧上，这个圆则是过 M'' 和 N'' 且与 x 轴相切的两个圆中较大的那一个，即还存在一个半径更小的过 M'' 和 N'' 且与 x 轴相切的圆. 以下整理成一个引理并给出证明.

引理：如下图所示，半径为 CE 的 圆 C 与水平直线 FL 相切于点 F，M 和 N 是圆上位于直径 EF 右侧的两点，且 N 在 M 的左下侧. D 是 MN 的中点，CD 的延长线过点 L. 则线段 LC （不含端点）上存在唯一的点 P 使得以 P 为圆心以 P 到 FL 的距离为半径的圆过点 M 和 N，且点 N 一定在该圆的左半侧.

 

证明：设动点 P 从点 L 沿着 LC 线段往上移动，以 LP 的长度为自变量 x，则 P 到 FL 的距离为：f(x) = x·sin∠CLF.

PM 的距离为：g(x) = (MD² + PD²)^1/2 = (MD² + (x - DL)²)^1/2. 其中 sin∠CLF，MD，DL 都是大于 0 的常数.

记 d = DL. 易知 f(x) 和 g(x) 都是 [0, +∞) 上的连续函数. f(x) 在 [0, +∞) 上单调递增；g(x) 在 [0, d) 上单调递减， 在 [d, +∞) 上单调递增.

且显然有 f(0) < g(0). 过点 N 作 FL 的垂线，分别交 CL 和 FL 于点 J 和点 K. 如下图所示：

显然有 JK > JN = JM. 记 j = LJ，即有 f(j) > g(j). 于是结合上述连续函数 f(x) 和 g(x) 的单调性，以及 f(0) < f(0)，可知存在 t ∈ (0, j)，使得 f(t) = g(t).

对应到上图，就是在线段 LJ 上必定存在一点 P 使得 P 到 FL 的距离等于 PM，即以 P 为圆心 PM 为半径的圆过点 M 和 N 且与 FL 相切. 而 点 N 显然在该圆的左半侧. 至此，引理得证.

下图是 f(x) 和 g(x) 的示意图，图中点 D 的横坐标为 d，J₁ 和 J₂ 的横坐标为 j. 

 综上，最大张角点的存在性得证. 且有以下结论：

(1). c = 0（即 MN 所在直线垂直于 x 轴）时，存在两个半径相等的过 M 和 N 且和 x 轴相切的圆，半径都等于 MN 的中点 D 到 x 轴的距离.  两个圆与 x 轴的切点都是最大张角点.

(2).  a = b（即 M 和 N 等高）时，存在唯一一个过 M 和 N 且和 x 轴相切的圆，切点为唯一的最大张角点.

(3). a ≠ b 且 c ≠ 0（即 M 和 N 不等高且 MN 所在直线不与 x 轴垂直）时，存在两个半径不相等的过 M 和 N 且和 x 轴相切的圆，半径小的圆与 x 轴的切点是唯一的最大张角点. 

接下来证明最大张角点的尺规可作性.

关于尺规可作性的理论基础，这里从冯承天老师所著的《从一元一次方程到伽罗瓦理论》 截取一段，如下图所示：

在本题中，已知三个可作数：a，b，c. 不妨令 a 为单位长度，即 a = 1.

对照上面的三种情形，逐个来看一下：

(1). c = 0（即 MN 所在直线垂直于 x 轴）时，存在两个半径相等的过 M 和 N 且和 x 轴相切的圆，半径都等于 MN 的中点 D 到 x 轴的距离.  两个圆与 x 轴的切点都是最大张角点.

此种情形下的两个最大张角点显然是尺规可作的.

(2). a = b（即 M 和 N 等高）时，存在唯一一个过 M 和 N 且和 x 轴相切的圆，切点为唯一的最大张角点.

对应的示意图如下：

由前面的分析可知 x = (v² + w) / (2v)  就是符合要求的唯一圆的半径长度，v = a + b，由 a 和 b 可作，v 也是可作的，于是 v² = v·v，2v = v + v 也都是可作的；同样地， w = c² + (a - b)² 也是可作的. 因而 x = (v² + w) / (2v) 是可作的. 以点 M 为圆心 x 为半径作圆弧交 MN 的垂直平分线于点 P，再以点 P 为圆心 x 为半径作圆，与 x 轴的交点 Q 即为所求的最大张角点.

(3). a ≠ b 且 c ≠ 0（即 M 和 N 不等高且 MN 所在直线不与 x 轴垂直）时，存在两个半径不相等的过 M 和 N 且和 x 轴相切的圆，半径小的圆与 x 轴的切点是唯一的最大张角点. 

由前面的分析可知，此种情形下就是要证明 x₂ = [2uv - Δ^1/2] / (k²) 是尺规可作的.

由 u = k² + 1，v = a + b，w = c² + (a - b)²，k = (a - b) / c，Δ = 4u²v² - 4(u - 1)(uv² + w) 可知

k，k²，u，v，w，Δ 都是可作的，由 Δ 可作，Δ^1/2 也可作. 于是 x₂ 也是可作的.

至此，命题已完成证明. 

 

 -----------------------------------------------------------------------------------------------

以下是分析过程中的一些其它结论，放在最后算作花絮：

假设存在过点 M 和 N 且与 x 轴相切的圆，该圆的圆心记为 P，该圆的半径记为 r，则点 P 的坐标可记为 (p, r). 于是

r² = PM² = PD² + DM² = (c - p)² + (a + b - r)² + (2c - c)² + (2a - a - b)² 

   = c² + p² - 2cp + (a + b)² + r² - 2(a+b)r + c² + (a - b)² 

   = 2c² + p² - 2cp + 2a² + 2b² + r² - 2(a+b)r

化简后，即为

⑤'      2(a+b)r = 2(a² + b² + c²) + p² - 2cp.

由前述分析可知，P 在直线 CD 上，故有

⑥'     cp + (a-b)r = a² - b² + c².

由 ⑥' 有 cp = a² - b² + c² - (a-b)r，代入 ⑤'，可得 4br = 4b² + p²，即

⑦'     r = b + p²/(4b).

由 ⑦' 可知 r ≥ b. 上面的分析过程并没有约定 a 和 b 的大小关系，把 a 和 b 互换（对应把线段 MN 沿中点 D 到 x 轴的垂线作对称变换后，再把 M 称作 N，N 称作 M 的情形 ），即 N 和 M 调整后的坐标为：N(0, 2a)，M(2c, 2b)，设点 P 的坐标为 (q, r)，重复上面的分析过程可得

⑧'    r = a + q²/(4a).

综合 ⑦' 和 ⑧'，即有

⑨'    r ≥ max{a, b}. 

结论 ⑨' 在几何上是很直观的. 就是过 M 和 N 且和 x 轴相切的圆的最高点一定不低于 M 和 N，即 2r ≥ max{2a, 2b}.