Rudin 数学分析原理定理 4.19 （紧集上的连续函数是一致连续函数）的证明思路分析

f: X→Y 是连续函数，X、Y是度量空间，且 X 是紧集，则 f 在 X 上一致连续.

分析：任意给定 ε > 0，由 f 的连续性可知，对任意一点 p ∈ X，存在 ζ(p) > 0 使得

①    若 q ∈ X 满足 d_X(p, q) < ζ(p)，则 d_Y(f(p), f(q)) < ε.

把点 p 的邻域 N(p, ζ(p), X) 记为 V(p)，则 {V(p): p ∈ X} 显然是 X 的一个开覆盖，由 X 是紧集可知，{V(p): p ∈ X} 中存在 X 的一个有限子覆盖，不妨记为 {V(s_i): s_i ∈ X, i = 1,2,...,k, k ∈ Z⁺}，即有

②    X ⊂ V(s₁) ∪ ... ∪ V(s_k).

而 f 在 X 上的一致连续性要求对任意给定 ε > 0，存在 δ(ε) 使得

③    若 s, t ∈ X，满足 d_X(s, t) < δ(ε)，则 d_Y(f(s), f(t)) < ε.

就 s 而言，由 ② 可知存在一个整数 j，满足 1≤ j ≤ k，并使得 s ∈ V(s_j). 即 s 落在邻域 V(s_j) 中. 取 δ(ε) = min(ζ(s₁), ..., ζ(s_k))，则由 d_X(s, t) < δ(ε) 可知 s 和 t 的距离小于 V(s_j) 的半径（即 ζ(s_j)），但不能保证 t 也落在 V(s_j) 中，例如下图所示的情形：

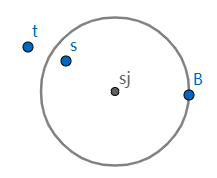
事实上，不论 δ(ε) 取得多小，都不能确保 s、t 都落在 V(s_j) 中. 因此，对上面的开覆盖的选取还需优化一下，即取颗粒更细的开覆盖. 比如，记 J(p) = N(p, ζ(p) / 2, X)，即 J(p) 的半径是 V(p) 的半径的一半，{J(p)} 显然也是 X 的一个开覆盖，同样，{J(p)} 中存在 X 的一个有限子覆盖，不妨记为 {J(p_i): p_i ∈ X, i = 1,2,...,n, n ∈ Z⁺}，即有

②'    X ⊂ J(p₁) ∪ ... ∪ J(p_n).

重新考察 ③，就 s 而言，由 ②' 可知存在一个整数 j，满足 1≤ j ≤ n，并使得 s ∈ J(p_j). 即 s 落在邻域 J(p_j) 中. 取 δ(ε) = min(ζ(p₁), ..., ζ(p_n)) / 2，则由 d_X(s, t) < δ(ε) 可知 t 一定落在 V(p_j) 中（尽管不能保证 t 落在 J(p_j) 中）， 如下图所示：

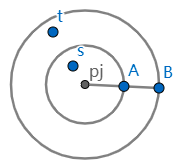
事实上，d_X(p_j, t) < d_X(p_j, s) + d_X(s, t) < ζ(p_j) / 2 + δ(ε) < ζ(p_j).

于是结合 ①，便有

d_Y(f(s), f(t)) < d_Y(f(p_j), f(s)) + d_Y(f(p_j), f(t)) < ε + ε = 2ε.