一道几何题的简单解法

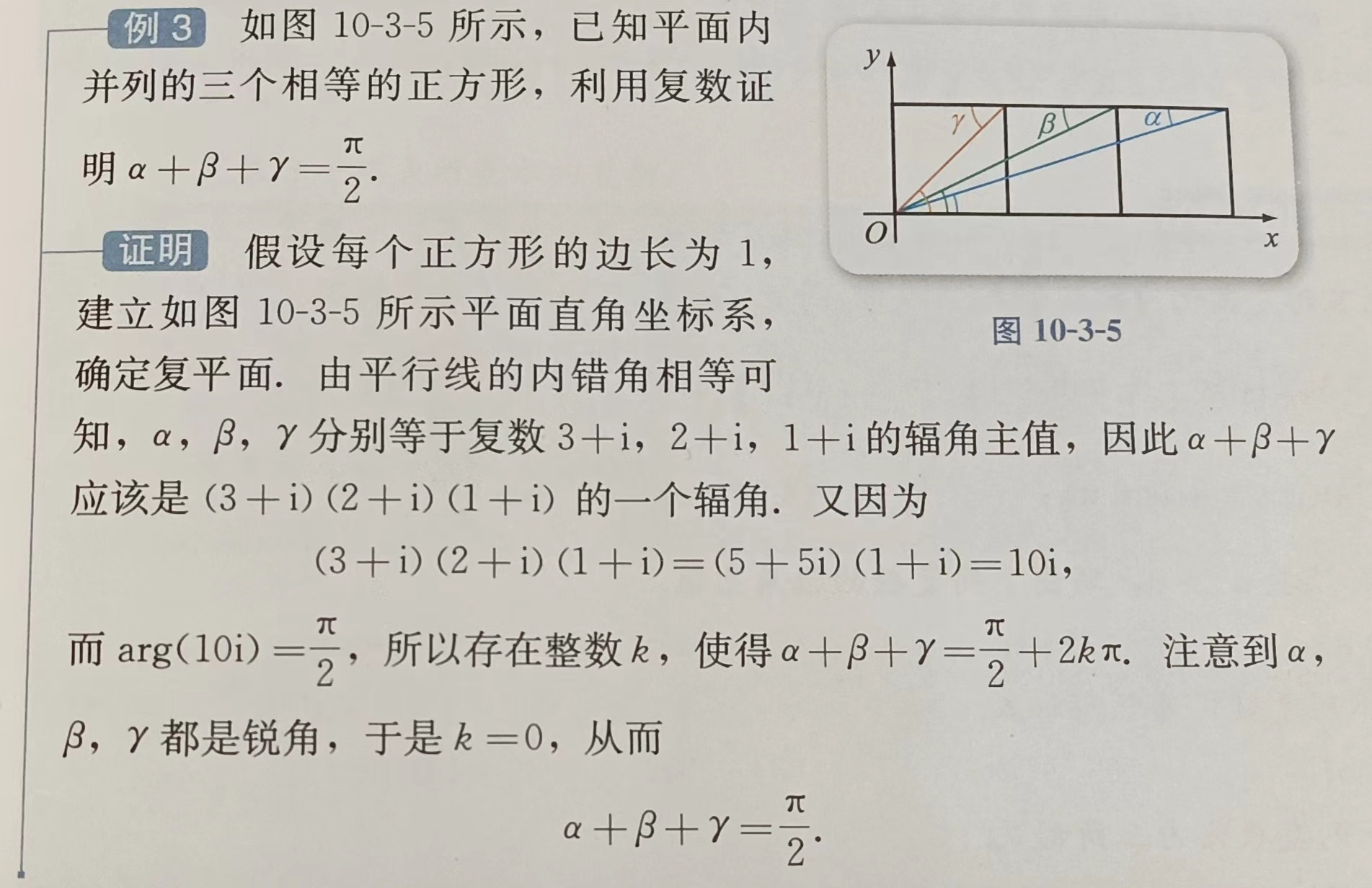
这是高中数学教材复数部分的一个例题. 以下是该题的一个简单的初中解法：

如下图所示，原题等价于证明 ∠CHA + ∠CDA = 45°，即等价于 ∠CHA = ∠FAD.

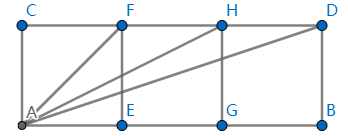
在直角三角形 CHA 中，短直角边 AC 是长直角边 CH 的 1/2（即 tan ∠CHA = 1/2），因此为 ∠FAD 构造一个同比例的直角三角形是一个求解思路.  延长 GH 和 AF，交于点 I，连接 DI. 如下图所示：

 

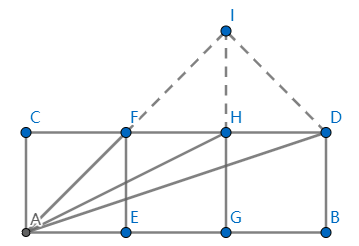
 易知 HIF 和 HID 均为等腰直角三角形， ∠AID = ∠FIH + ∠HID = 90°，且有 AI = 2·DI，即有 △CHA ∽ △IAD. 于是有 ∠CHA = ∠FAD. 即有 ∠CHA + ∠CDA = 45°，即  ∠CFA + ∠CHA + ∠CDA = 90°.