基础拓扑习题与题解（二）

以下习题选自Walter Rudin 所著的 《Principles of Mathematical Analysis Third Edition》（数学分析原理第三版）的第二章：基础拓扑（Basic Topology）习题集.

习题 21

设 R^k 中的两个子集 A 和 B 是分离的. a ∈ A，b ∈ B.  定义
    p(t) = (1 - t)a + tb, t ∈ R¹.
记 A₀ = p^-1(A)，B₀ = p^-1(B). 则
(a) A₀ 和 B₀ 是 R¹ 中的两个分离子集.
(b) 存在 t₀ ∈ (0, 1) 满足 p(t₀) ∉ A ∪ B.
(c) R^k 中凸集一定是连通集.

分析：(a) 和 (b) 为 (c) 的证明提供了切实可行的思路. 双射 p 把 R¹ 上的点（数）映射为直线 ab 上的点. 这样，R^k 中两个分离的子集可以对应到 R¹ 中两个分离的子集. 下面是一个直观的示意图：

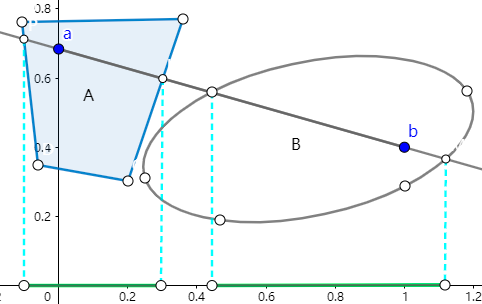
 证明：(a) 假设 A₀ 和 B₀ 不是分离的，则 A^¬₀ ∩ B₀ ≠ Φ 或者 A^¬₀ ∩ B₀ ≠ Φ. 不失一般性，不妨设 A^¬₀ ∩ B₀ ≠ Φ，即存在 x ∈ R¹ 满足 x ∈ A^¬₀ 以及 x ∈ B₀. 由 x ∈ A^¬₀ 可知，要么 x ∈ A₀，要么 x 是 A₀ 的极限点.
若 x ∈ A₀，则 p(x) ∈ A，由 x ∈ B₀，又有 p(x) ∈ B，即 A ∩ B ≠ Φ，与 题设（A 和 B 是分离的）矛盾；若 x ∉ A₀ 但 x 是 A₀ 的极限点，即 x 的任意邻域 N(x, δ, R¹) 都含有 A₀ 中的点，即存在 y ∈ A₀ 满足 |x - y| < δ，于是
   ①       |p(x) - p(y)| = |(1 - x)a + xb - (1 - y)a - yb| = |a - b|·|x - y| < |a - b|·δ.
由 y ∈ A₀，有 p(y) ∈ A，由 ① 可知，p(x) 是 A 的极限点（对任意 ε > 0，取 δ = ε / |a - b|，就有 |p(x) - p(y)| < ε），即 p(x) ∈ A^¬；而由 x ∈ B₀，有 p(x) ∈ B，与 题设（A 和 B 是分离的）矛盾.

(b) 假设任意 t ∈ (0, 1) 都满足 p(t) ∈ A ∪ B，即 p(t) ∈ A 或 p(t) ∈ B. 由题设可知，任意 t ∈ (0, 1) 都满足 t ∈ A₀ 或 t ∈ B₀，即有 (0, 1) ⊂ A₀ ∪ B₀. 由题设显然有 0 ∈ A₀，1 ∈ B₀，于是有 [0, 1] ⊂ A₀ ∪ B₀. 记 C₀ = [0, 1]，C₁ = C₀ ∩ A₀，C₂ = C₀ ∩ B₀. 则
  ②      C₀ = C₀ ∩ (A₀ ∪ B₀) = (C₀ ∩ A₀) ∪ (C₀ ∩ B₀) = C₁ ∪ C₂.
由 A₀ 和 B₀ 分离可知，C₁ 和 C₂ 是分离的，显然 0 ∈ C₁，1 ∈ C₂，即 C₁ 和 C₂ 都是非空集，结合 ② 可推知，C₀ 不是连通集，但 C₀ = [0, 1] 显然是连通集，矛盾.

(c) 假设 R^k 中凸集 E 不是连通集，即存在 R^k 中分离的两个非空子集 A 和 B 满足 E = A ∪ B. 取 a ∈ A，b ∈ B， 由 (b) 可知，存在 t₀ ∈ (0, 1) 满足 (1 - t₀)a + t₀b ∉ E. 这与 E 是凸集矛盾.

习题 22

若度量空间 E 的某个稠密子集 D 是可数集，则称 E 是可分的（separable）. 求证：R^k 是可分的.

证明：Q^k ⊂ R^k 是可数集，只需证明 Q^k 在 R^k 中稠密. 任取 R^k 中一点 p = (x₁, x₂, ^..., x_k)，从 Q^k 中取一点 q = (q₁, q₂, ^..., q_k)，其中 x_i ∈ R，q_i ∈ Q，i = 1, 2, ^..., k. 则 |p - q|² =  Σ _i=1..k [(x_i - q_i)²].
给定任意小的正实数 ε，对任意 x_i ∈ R，存在 q_i ∈ Q，使得 (x_i - q_i)² < ε² / k. 即有 
|p - q|² < k·(ε² / k) = ε²，即 |p - q| < ε. 由 ε 的任意性，可知 Q^k 在 R^k 中是稠密的.

习题 23

X 的一组开子集 {V_α} 称作 X 的一个基（base），若满足以下条件：
对任意 x ∈ X 以及 X 中的含有 x 的开集 G，存在某个 V_α 使得 x ∈ V_α ⊂ G. 或者说，X 中的每一个开集都是 {V_α} 的一个子组集合的并集.
求证：可分的度量空间一定存在一个可数基.

证明：设度量空间 X 是可分的，则 X 存在某个可数稠密子集 D. 对任意 y ∈ D 以及任意正有理数 q，构造邻域 N(y, q, X)，得到 X 的一组开子集 Δ = {N(y, q, X) | y ∈ D, q ∈ Q}，D 和 Q 都是可数的，则 Δ 也是可数的. 剩下只需证明 Δ 是 X 的基. 

任取 x ∈ X，以及 X 中的含有 x 的开集 G，则存在 x 的某个邻域 N(x, r, X) 满足 N(x, r, X) ⊂ G.
(1)  若 x ∈ D，取 q ∈ Q 且 满足 0 < q < r，则有 x ∈ N(x, q, X) ⊂ N(x, r, X) ⊂ G，且 N(x, q, X) ∈ Δ；
(2) 若 x ∉ D，则 x 是 D 的极限点，邻域 N(x, r/8, X) 有点 z ∈ D，易知
   x ∈ N(x, r/8, X) ⊂ N(z, r/4, X) ⊂ N(z, r/2, X) ⊂ N(x, r, X) ⊂ G.
【以证明 N(x, r/8, X) ⊂ N(z, r/4, X) 为例：对任意 p ∈ N(x, r/8, X)，则 |z - p| ≤ |x - z| + |x - p| < r/8 + r/8 = r/4，即有 p ∈ N(z, r/4, X) 】
取 q ∈ Q 且 满足 r/4 < q < r/2，则有 x ∈ N(z, q, X) ⊂ N(x, r, X) ⊂ G，且 N(z, q, X) ∈ Δ.
综合 (1) 和 (2)，可知 Δ 是 X 的基.

习题 24

度量空间 X 为无限集，且其任意无限子集在 X 中都存在极限点. 则 X 是可分的.

证明：给定一个正实数 r，构造 X 的一个子集 E_r，使其包含尽可能多的点并满足其中任意两点的距离均 ≥ r. 具体做法如下：
步骤 i（i 从 1 开始计数）：从 X_i （X₁ = X）中任取一点 x_i ∈ X_i 加入 E_r，记 X_i+1 = X_i - N(x_i, r, X)，若 X_i+1 为空，则 E_r 构造完成；否则，i 的计数加1，继续 步骤 i.
由题设可知，E_r 一定是有限集. （不然，E_r 存在极限点 p 可使邻域 N(p, r/2, X) 含有 E_r 中无限个点，选取其中两点 x 和 y，则 |x - y| ≤ |p - x| + |p - y| < r/2 + r/2 = r，与 E_r 的构造要求矛盾.）
记 E_r = {x₁, x₂, ^..., x_k}，且对任意 q ∈ E_r^c(X)，必然存在某个 x ∈ E_r 使得 |x - q| < r，即 q ∈ N(x, r, X). 于是 X = ∪ _i=1..k N(x_i, r, X). 

【以上实际上顺带证明了 X 是有界集.】

取 r = 1, 1/2, ^..., 1/n, ^...，由上面的构造法得到对应的 E₁, E_1/2, ^..., E_1/n, ^.... 取 D = ∪ _i=1.._∞ E_1/i. 显然，D 是可数集. 剩下只需证明 D 在 X 中稠密. 对任意 x ∈ X - D，以及 ε > 0，存在自然数 k 使得 1/k < ε，且 E_1/k 中存在一点 y 使得 x ∈ N(y, 1/k, X)，即有 |x - y| < 1/k < ε，由 ε 的任意性可知 x 是 D 的极限点. 因此，D 在 X 中稠密.

习题 25

若紧集 K 是无限集，则 K 一定有一个可数基，并因此是可分的.

证明：对任意正实数 r，由 K ⊂ ∪ _x∈K N(x, r, K) 和紧集定义可知，存在 K 的有限子集 E(r) = {x₁, x₂, ^..., x_k} 使得 K ⊂ ∪ _i=1..k N(x_i, r, K) = ∪ _x∈E(r) N(x, r, K).
记 V(r) = {N(x, r, K) | x ∈ E(r)}，V = ∪ _i=1.._∞ V(1/i) ，V 中任意元素显然是 K 的开子集，且 V 是可数的. 对任意 y ∈ K 以及含有 y 的开子集 G ⊂ K，由开集性质可知，存在正实数 δ 使得 N(y, δ, K) ⊂ G，取正整数 m 满足 1/m < δ/2，记 V(1/m) 中含有 y 的某个邻域为 M = N(z, 1/m, K)，任取 p ∈ M，则有
   |y - p| ≤ |z - y| + |z - p| < 1/m + 1/m < δ. 

即有 p ∈ N(y, δ, K). 从而有 y ∈ M ⊂ N(y, δ, K) ⊂ G. 
综上可知，V 是 K 的一个可数基.

取 D = ∪ _i=1.._∞ E(1/i). 显然，D 是可数的，且有 D ⊂ K. 任取 y ∈ K - D，以及 ε > 0，取正整数 m 满足 1/m < ε，记 V(1/m) 中含有 y 的某个邻域为 M = N(z, 1/m, K)，显然 z ∈ D，且 |z - y| < 1/m < ε，即 z ∈ N(y, ε, K) ∩ D. 因此，y 是 D 的极限点. 由 y 的任意性可知，D 在 K 中稠密.
综上，K 是可分的.