紧集笔记（二）

引

继 紧集（compact sets）笔记（一） 之后，一个自然的目标是证明 Walter Rudin 所著的 《Principles of Mathematical Analysis Third Edition》（以下简称为教材）里给出的紧集定义和上次笔记里给出的紧集定义一是等价的. 具体可以分解为如下两个命题：

命题一：若子集 K 在度量空间 X 中的任意一个开覆盖都包含一个可以覆盖 K 的有限子覆盖，则 K 是有界的，且对于任意包含 K 的 度量空间 Y，K 都是闭集.

命题二：K 是度量空间 X 的子集，若 K 是有界的，且对于任意包含 K 的 度量空间 Y，K 都是闭集，则 K 在 X 中的任意一个开覆盖都包含一个可以覆盖 K 的有限子覆盖.

一些符号约定

邻域 N(p, r, X)

若 X 为一个度量空间，p ∈ X，r 为正实数，则记 N(p, r, X) = {q | d(p, q) < r, q ∈ X}，这实际上就是教材里邻域的定义. 但因为邻域是个相对的概念，在符号定义里显式给出所基于的度量空间，会带来表达上的便利.

补集 E^c(X)

E ⊂ X，记 E^c(X) = {p | p ∈ X, p ∉ E}.

开集的特性

已知 E ⊂ Y ⊂ X，X 是度量空间，若 E 相对 X 是开集，即任取 p ∈ E，存在 r > 0，使得 N(p, r, X) ⊂ E，由 Y ⊂ X 可知 N(p, r, Y) ⊂ N(p, r, X)，因而有 N(p, r, Y) ⊂ E，即 E 相对 Y 也是开集. 但反过来，若 E 相对 Y 是开集，并不能推出 E 相对 X 也是开集. 这正说明了开集是个相对的概念. 具体来看两个示例. 

示例1

E = (0, 1) ∩ Q，Y = Q，X = R

这里 E 是开区间 (0, 1) 中全体有理数的集合. 任取 p ∈ E，记 r_p = min(d(p, 0), d(p, 1))，则显然有 N(p, r_p, Q) ⊂ E，即 E 相对 Y 是开集. 但无论 r 取多小，N(p, r, R) 中总有无理数，即 N(p, r, R) ⊂ E 不成立，E 相对 X 不是开集.

示例2

E = {(x, y) | x = y, x ∈ (0, 1)}，Y = {(x, y) | x = y, x ∈ R}，X = R²

这里 Y 是 R² 中一条直线 y = x，如下图所示，E 是这条直线上的一截不含端点 a 和 b 的线段.

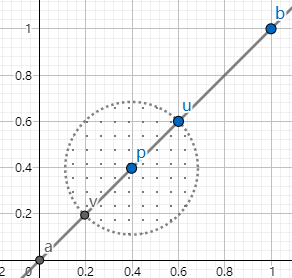
任取 p ∈ E，记 r_p = min(d(p, a), d(p, b))，显然有 N(p, r_p, Y) ⊂ E，即 E 相对 Y 是开集. 但无论 r 取多小，N(p, r, X) 中总有线段之外的点，即 N(p, r, X) ⊂ E 不成立，E 相对 X 不是开集.

示例 2 中，N(p, r, Y) 是以点 p 为中点的一截线段（不含两端端点），而 N(p, r, X) 是以点 p 为圆心的一个实心圆体（不含外围点）.

定理 2.30

已知 E ⊂ Y ⊂ X，X 为一个度量空间. E 相对 Y 是开集当且仅当存在一个 X 的子集 G 满足 G ∩ Y = E 且 G 相对 X 是开集.

证明：先证充分性. 任取 p ∈ E，由 G ∩ Y = E 可知 p ∈ G，而 G 相对 X 是开集，于是存在 r > 0 使得：

N(p, r, X) ⊂ G

两端与 Y 取交集，N(p, r, X) ∩ Y ⊂ G ∩ Y，即 N(p, r, Y) ⊂ E，E 相对 Y 是开集.

必要性的证明比较麻烦，涉及 G 的构造.  由 G ∩ Y = E 可知 E ⊂ G，一个思路是对 E 作扩充得到 G，具体如下：

E 相对 Y 是开集，故对任意 p ∈ E，存在 r_p > 0，使得 N(p, r_p, Y) ⊂ E. 对 E 中每个点的这种邻域求并集

∪_p∈E N(p, r_p, Y)，因为其中的每个邻域都有 N(p, r_p, Y) ⊂ E，所以 ∪_p∈E N(p, r_p, Y) ⊂ E；另一方面，E 中任意一个点 p 都满足 p ∈ N(p, r_p, Y)，由此可知，E ⊂ ∪_p∈E N(p, r_p, Y). 因此，E = ∪_p∈E N(p, r_p, Y).

记 G_p = N(p, r_p, X)，G = ∪_p∈E N(p, r_p, X). 

G_p 相对 X 是开集，G 相对 X 也是开集. G ∩ Y = ∪_p∈E (N(p, r_p, X) ∩ Y) =  ∪_p∈E N(p, r_p, Y) = E. 证毕.

扩展分析：闭集的特性

已知 E ⊂ Y ⊂ X，X 是度量空间，若 E 相对 X 是闭集，假设点 p ∈ Y 是 E 的极限点，由 Y ⊂ X 可知 p ∈ X，再由 E 相对 X 是闭集，可知 p ∈ E，因而 E 相对 Y 也是闭集. 但反过来，若 E 相对 Y 是闭集，并不能推出 E 相对 X 也是闭集. 这正说明了闭集是个相对的概念. 对照上面开集的特性部分来看一下对应的示例. 

示例1

E = [0, 1] ∩ Q，Y = Q，X = R

这里 E 是闭区间 [0, 1] 中全体有理数的集合. E 中每个点都是 E 的极限点，且 E 在 Y 中没有其它的极限点，因此 E 相对 Y 是闭集. 但 E 在 X 中还有很多极限点，比如 π / 4，它们都不属于 E，因此 E 相对 X 不是闭集.

示例2

E = {(x, y) | x = y, x ∈ [0, 1]}，Y = {(x, y) | x = y, x ∈ R}，X = R²

这里 Y 是 R² 中一条直线 y = x，E 是这条直线上的一截含端点 (0, 0) 和 (1,1) 的线段. 容易验证 E 相对 Y 是闭集，相对 X 也是闭集. 事实上，本例中 E 是紧集，即 E 相对任意包含 E 的度量空间都是闭集.

闭集的情形是否存在类似定理 2.30 的定理？

命题三：已知 E ⊂ Y ⊂ X，X 为一个度量空间. E 相对 Y 是闭集当且仅当存在一个 X 的子集 G 满足 G ∩ Y = E 且 G 相对 X 是闭集.

分析：先看充分性. 假设 X 的子集 G 满足 G ∩ Y = E 且 G 相对 X 是闭集. 把 G 中的全体孤立点的集合记为 S，全体极限点的集合记为 L，则 G = S ∪ L，且 S ∩ L = Φ.

S 可以进一步划分为 S₁ 和 S₂，其中 S₁ = S ∩ Y，S₂ = S₁^c(S).

同样，L 进一步划分为 L₁ 和 L₂，其中 L₁ = L ∩ Y，L₂ = L₁^c(L).

于是 E = G ∩ Y = S₁ ∪ L₁. 

假如 E 相对 Y 不是闭集，则存在某点 p ∈ Y 是 E 在 Y 上的极限点，但 p ∉ E，即有 p ∉ L₁. 由极限点定义可知，N(p, r, Y) 中总有 E 中的点；再由 E ⊂ G 和 Y ⊂ X，可知 p 也是 G 在 X 上的极限点，故 p ∈ L，结合 p ∉ L₁，可知 p ∈ L₂ ；而 L₂ ∩ Y = Φ. 这与 p ∈ Y 矛盾. 因此，命题一的充分性成立.

再看必要性.  假设 E 相对 Y 是闭集. 按孤立点和极限点划分，E 分为 S 和 L 两个子集，记 E 在 X 上的全体极限点的集合为 F，由 Y ⊂ X  以及 E 相对 Y 是闭集，可知 F ∩ Y = L.

取 G = F ∪ S，则显然有 G ⊂ X，且 G 相对 X 是闭集，以及 G ∩ Y = (F ∪ S) ∩ Y = L ∪ S = E. 必要性同样成立.

因此，命题三可称为定理 2.30 的平行定理.

定理 2.33

已知 K ⊂ Y ⊂ X，X 为一个度量空间. K 相对 Y 是紧集当且仅当 K 相对 X 是紧集.

在紧集定义一中，直接由定义本身（对于任意包含 K 的 度量空间 Y，K 都是闭集）保障了紧集不是个相对的概念，因此定理 2.33 的结论是显然的. 但由教材里的紧集定义，定理 2.33 的结论并不是显然的.

证明：先证充分性：由 K 相对 X 是紧集推出 K 相对 Y 是紧集. 假设 {Gα} 是 K 在 Y 中的一个开覆盖，其中每个 Gα 相对 Y 是开集，由上面的桥接定理可知存在相对 X 的开集 Vα 满足 Gα = Vα ∩ Y.

由 K ⊂ ∪_α G_α ⊂ ∪_α V_α， 可知 {Vα} 是 K 在 X 中的一个开覆盖，由 K 相对 X 是紧集知 {Vα} 包含一个可以覆盖 K 的有限子覆盖，不妨设 K ⊂ Vα₁ ∪ ... ∪ Vα_n，两边与 Y 取交集，有 K ∩ Y ⊂ (Vα₁ ∩ Y) ∪ ... ∪ (Vα_n ∩ Y)，即 K ⊂ Gα₁ ∪ ... ∪ Gα_n，至此可知 K 相对 Y 是紧集.

再证必要性：由 K 相对 Y 是紧集推出 K 相对 X 是紧集. 假设 {Vα} 是 K 在 X 中的一个开覆盖，其中每个 Vα 相对 X 是开集，即有 K ⊂ ∪_α V_α，两边与 Y 取交集，有 K ∩ Y ⊂ ∪_α (V_α ∩ Y). 记 Gα = Vα ∩ Y，即有 K ⊂ ∪_α G_α.

Gα ⊂ Y ⊂ X，由上面的桥接定理可知 Gα 相对 Y 是开集. 于是 {Gα} 是 K 在 Y 中的一个开覆盖. 由 K 相对 Y 是紧集知  {Gα} 包含一个可以覆盖 K 的有限子覆盖，不妨设 K ⊂ Gα₁ ∪ ... ∪ Gα_n，由 Gα = Vα ∩ Y 知 Gα ⊂ Vα. 因此，K ⊂ Gα₁ ∪ ... ∪ Gα_n ⊂ Vα₁ ∪ ... ∪ Vα_n，至此可知  K 相对 X 是紧集.

定理 2.34 紧集是闭集

紧集定义一中，直接用闭集来定义紧集（对于任意包含 K 的 度量空间 Y，K 都是闭集），因此定理 2.34 的结论是显然的. 但由教材里的紧集定义，定理 2.34 的结论并不显然.

证明：设度量空间 X 的子集 K 是紧集，任意取定一点 p ∈ K^c(X)，对 K 中的每一个点 q_α，以 0 < r_α < d(p, q_α)/2 为半径构造邻域 W_α = N(q_α, r_α, X)，则有 K ⊂ ∪_α W_α，即 {W_α} 是 K 在 X 上的一个开覆盖，显然这个开覆盖没有覆盖点 p. 由 K 是紧集，不妨设 K ⊂ W₁ ∪ ... ∪ W_n = W，其中 W_i = N(q_i, r_i, X)，i = 1, ..., n. 相应地，构造点 p 的 n 个邻域：V_i = N(p, r_i, X)，i = 1, ..., n；并令 V = V₁ ∩ ... ∩ V_n，由上述对半径的约束可知 W_i 和 V_i 是分离的（separated），进而可知 V ∩ W = Φ，结合 K ⊂ W 有 V ∩ K = Φ，即 V ⊂ K^c. 再结合 V 是开集，以及 p ∈ V，可知 K^c 是开集，即 K 是闭集.

定理 2.35 紧集的闭子集是紧集

证明： 已知 E ⊂ K ⊂ X，K 是紧集，E 相对 K 是闭集. 设 {V_α} 是 E 在 X 上的一个开覆盖，即 E ⊂ ∪_α V_α，两边取与 K 的交集，有：

①          E ⊂ ∪_α (V_α ∩ K).

V_α 相对 X 是开集，由定理 2.30 可知，V_α ∩ K 相对 K 是开集，即 {V_α ∩ K} 是 E 在 K 上的一个开覆盖，① 的两边并上 E^c(K)，有：

②         K ⊂ ∪_α (V_α ∩ K) ∪ E^c(K).

E 相对 K 是闭集，E^c(K) 相对 K 是开集. 记 G_α = V_α ∩ K，由 ② 可知，{G_α} 搭上 E^c(K) 构成 K 在 K 上的一个开覆盖. 由 K 是紧集，不妨设 K ⊂ G₁ ∪ ... ∪ G_n ∪ E^c(K).

显然有 G_i ⊂ V_i，i = 1, ..., n. 故有 E ⊂ G₁ ∪ ... ∪ G_n ⊂ V₁ ∪ ... ∪ V_n. 因此 E 是紧集. 证毕.

教材中对这个定理的证明，给出的假设是：Suppose F ⊂ K ⊂ X, F is closed (relative to X), and K is compact. 其中标黄部分（对照教材中定理 2.35 的原文：Closed subsets of compact sets are compact.）是不够严谨的：在 F ⊂ K ⊂ X 的前提下，F 相对 X 是闭集，则 F 相对 K 也是闭集；但 F 相对 K 是闭集，则 F 相对 X 不一定是闭集（参考上面的扩展分析：闭集的特性）.

推论  若 E ⊂ X，K ⊂ X，E 相对 X 是闭集，K 是紧集，则 E ∩ K 是紧集.

证明：由定理 2.34 知 K 是闭集，由题设 E 是闭集，故  E ∩ K 相对 X 是闭集，由闭集的特性知 E ∩ K 相对 K 也是闭集，由定理 2.35 知 E ∩ K 是紧集.

定理 2.36

若 {K_α} 是度量空间 X 的一组紧子集，且其中任意有限个集合的交集都不是空集，则 ∩ K_α 也不是空集.

证明：取定 {K_α} 中一个集合，记为 K₁，K₁ 显然不是空集，并记 G_α = K_α^c. 由定理 2.34 知每一个 K_α 都是闭集，因此，每一个 G_α 都是开集. 假设 ∩ K_α 是空集，则 K₁ 中没有同时属于每个 K_α 的点，即任给 p ∈ K₁，则 p 一定属于某一个 G_α. 于是 {G_α} 是 K₁ 的一个开覆盖，由 K₁ 是紧集，不妨设 K₁ ⊂ G₂ ∪ ... ∪ G_n，两边取补集有 K₁^c ⊃ K₂ ∩ ... ∩ K_n ，于是有 K₁ ∩ K₂ ∩ ... ∩ K_n = Φ，与题设矛盾.

推论  若 {K_n} 是一个非空紧集序列，且满足 K_n ⊃ K_n+1 (n = 1, 2, 3, ...)，则这个序列的全体集合的交集 ∩ _n=1,...,∞ K_n  不为空.

证明：从 {K_n} 中任意选定 m 个集合，对应的下标记为 α₁, ..., α_m，其中最大的下标记为 β，由题设可知这 m 个集合的交集就是 K_β，由定理 2.36 可知推论成立.

定理 2.37

若 E 是紧集 K 的无限子集，则 E 在 K 中有极限点.

证法一：假设 E 在 K 中没有极限点，由题设可知 E 由无限个孤立点组成. 于是 E 相对 K 是闭集. 而 K 是紧集，由定理 2.35 可知 E 是紧集. 对每个 p ∈ E，因为 p 是孤立点，都有一个邻域满足 V_p = {p}. 于是 E = ∪ V_p，即 {V_p} 构成 E 的一个开覆盖，但显然不存在一个覆盖 E 的有限子覆盖. 这与 E 是紧集矛盾.

证法二：假设 E 在 K 中没有极限点，那么对每个 q ∈ K，都有一个邻域 V_q 至多含有 E 中一个点（若 q ∈ E，即为 q）. 这样，{V_q} 构成 E 以及 K 的一个开覆盖，但显然不存在一个有限子覆盖可以覆盖 E （E 有无限个点，每个点对应一个 V_q），更无法覆盖 K（E 是 K 的子集），这与 K 是紧集矛盾.

这里的证法二就是教材里的证法.