求函数 f(θ) = (1 - sinθ) / (2 - cosθ) 的最小值和最大值.

求函数 f(θ) = (1 - sinθ) / (2 - cosθ) 的最小值和最大值.

解法一：由 sinθ ≤ 1 知 1 - sinθ ≥ 0，由 cosθ ≤ 1 知 2 - cosθ ≥ 1，于是 f(θ) ≥ 0，当 sinθ = 1 时，f(θ) = 0，所以 f(θ) 的最小值为 0.

令：

x = -2 + cosθ        ①

y = -1 + sinθ         ②

则 ① 和 ② 构成下图所示的单位圆的参数方程：

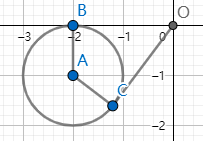
而 f(θ) = (1 - sinθ) / (2 - cosθ) = (-1 + sinθ) / (-2 + cosθ) = y / x

即 f(θ) 就是圆上一点与原点 O 的连线的斜率。从点 O 到这个圆有两条切线，即图中的 OB 和 OC，B、C 为切点。OB、OC 的斜率分别就是 f(θ) 的最小值和最大值。OB 的斜率显然为 0【注解1：记上图中坐标为 (-1, -1) 的点为 D，则此时 θ = ∠DAB = 2kΠ + Π/2】，来求 OC 的斜率。

 由 ①、② 可设点 C 的坐标为 (-2 + cosθ, -1 + sinθ)，则 AC 的斜率为

(-1 + sinθ + 1) / (-2 + cosθ + 2) = sinθ / cosθ

因为 AC ⊥ OC，所以

(sinθ / cosθ) · (-1 + sinθ) / (-2 + cosθ) = -1 ，即有

-sinθ + sin²θ = 2cosθ - cos²θ，即

sinθ + 2cosθ = 1

结合 sin²θ + cos²θ = 1，可求出 cosθ = 4/5，sinθ = -3/5，此时 OC 的斜率为

f(θ) = (1 - sinθ) / (2 - cosθ) = (8/5) / (6/5) = 4/3，这便是 f(θ) 的最大值【注解2：记上图中坐标为 (-1, -1) 的点为 D，则此时 θ = ∠DAC = 2kΠ - arccos(4/5)】。

解法二：记 t = (1 - sinθ) / (2 - cosθ)，则

2t - tcosθ = 1 - sinθ

2t - 1 = tcosθ - sinθ

令 cosψ = t / (t² + 1)^1/2，sinψ = 1 / (t² + 1)^1/2，则

(2t - 1) / (t² + 1)^1/2 = cosψ·cosθ - sinψ·sinθ = cos(ψ + θ)

由 (cos(ψ + θ))² ≤ 1，有

(2t - 1)² = 4t² - 4t + 1 ≤ t² + 1

即 t(3t - 4) ≤ 0

即 0 ≤ t ≤ 4/3

当 t = 0 时，cosψ = 0，sinψ = 1，cos(ψ + θ) = (2t - 1) / (t² + 1)^1/2 = -1，取  θ = ψ = Π/2，即满足要求；

当 t = 4/3 时，sinψ = 1 / [(4/3)² + 1]^1/2 = 3/5，cosψ = tsinψ = (4/3)·(3/5) = 4/5，cos(ψ + θ) = (2t - 1) / (t² + 1)^1/2 = 1，取 ψ = arccos(4/5)，并取 θ = -ψ，即可满足要求。

综上可知，f(θ) 的最小值和最大值分别为 0 和 4/3。

附言：

若对 f(θ) 按 (u/v)' = (u'v - uv') / (v²) 公式做求导，会得到 f'(θ) = (1 - sinθ - 2cosθ) /  (v²) ，反倒不好处理。