IMO 2021 第一题题解及相关拓展问题分析
IMO 2021 第 1 题:
设整数 n ≥ 100。伊凡把 n, n + 1, ..., 2n 的每个数写在不同的卡片上。然后他将这 n + 1 张卡片打乱顺序并分成两堆。证明:至少有一堆中包含两张卡片,使得这两张卡片上的数之和是一个完全平方数。
证:如果在 [n, 2n] 范围内存在 3 个整数 a、b、c,满足 a < b < c,且 a+b、a+c、b+c 都是完全平方数,则待证命题显然成立。考虑 a+b、a+c、b+c 是 3 个连续完全平方数的情形,由于 2 | a+b+a+c+b+c 知 居于中间位置的 a+c 必为偶数,令 a+c = (2k)2 = 4k2,k 为正整数,则 a+b = (2k-1)2,b+c = (2k+1)2,进而有
a = 2k2-4k,b = 2k2+1,c = 2k2+4k ①
由 a ≥ n 以及 c ≤ 2n,有 2(k-1)2 ≥ n+2,2(k+1)2 ≤ 2n+2,即有
1 + (n/2 + 1)1/2 ≤ k ≤ (n+1)1/2 - 1 ②
由 1 + (n/2 + 1)1/2 ≤ (n+1)1/2 - 1,可得出 n ≥ 48。但不能保证对每个大于等于 48 的 n 都有满足 ② 的 k 解,比如 n = 48,代入 ② 可得 k = 6,而 n = 49,则无 k 解。
为确保有 k 解,对 1 + (n/2 + 1)1/2 + 1 ≤ (n+1)1/2 - 1 求解,即
12(n+1)1/2 <= n + 18
542 - 180 <= (n - 54)2 ③
当n ≥ 54·2 = 108 时,③ 显然成立。即当 n ≥ 108 时,命题成立。
当 n = 100 时,② 的左侧为 1 + (51)1/2 ∈ (8,9),右侧为 (101)1/2 - 1 ∈ (9,10),易知 k 取值只能为 9,代入 ① 有 a = 126, b = 163 ,c = 198
当 n = 101,...,107 时,易知 126、163、198 也都在 [n, 2n] 范围内。
综上,命题得证。
以下为拓展分析部分:
拓展问题一:把 n, n + 1, ..., 2n 这 n + 1 个整数(n > 2)无论怎样分成两组,其中总有至少一组中存在两个数之和是一个完全平方数,请判断在这 n + 1 个整数中是否一定存在 3 个整数 a、b、c,满足 a < b < c,且 a+b、a+c、b+c 都是完全平方数。
考察上面提到的 n = 49 时无 k 解的情形,在 49, 50, ..., 98 中取两数相加,易知其和的最小值和最大值分别为 99 和 195,而在 [99, 195] 范围内有 4 个完全平方数:100、121、144、169,处在三个连续完全平方数的中间且为偶数的只有 144 = (2·6)2,对应前述 k = 6 的情形,代入 ① 可得 a = 48, b = 73, c = 96。但是 48 不在 [49, 98] 之内,这说明,在 49, 50, ..., 98 中不存在 3 个整数 a、b、c,满足 a < b < c,且 a+b、a+c、b+c 都是完全平方数。
以下试图把 49, 50, ..., 98 分到 A、B 两组,使得两组中都不存在两个数之和为完全平方数,A、B 互为对应组。
49 + 51 = 100 (I)
49→60 + 61←72 = 121 (II)
49→71 + 73←95 = 144 (III)
71→84 + 85←98 = 169 (IV)
把 49 放到 A 组,由 (I)、(II)、(III) 可知,51、72、95 都要放到 B 组,即
A: 49
B: 51, 72, 95
由 (II) 中的 51 + 70 = 121,以及 (III) 中的 51 + 93 = 144 可知,70、93 都要放到 A 组, 即
A: 49, 70, 93
B: 51, 72, 95
70 在 (III) 中,70 + 74 = 144,于是有
A: 49, 70, 93
B: 51, 72, 95, 74
72 在 (IV) 中,72 + 97 = 169,于是有
A: 49, 70, 93, 97
B: 51, 72, 95, 74
93 在 (IV) 中,76 + 93 = 169,于是有
A: 49, 70, 93, 97
B: 51, 72, 95, 74, 76
95 在(IV) 中,74 + 95 = 169,但是 74 和 95 已经在 B 组里了。
因此,由 n = 49 的情形分析可知,拓展问题一的答案是否定的。
对上述过程稍作提炼可知,49、51、70、74、95 这 5 个数由于 49+51、51+70、70+74、74+95、95+49 都是完全平方数,可形象地把这 5 个数(用更一般的 a、b、c、d、e 替代)排成五边形,则该五边形的每条边上的两数和(a+b、b+c、c+d、d+e、e+a)都是完全平方数。如下图所示:
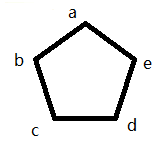
若把 a 放到 A 组,为避免 A 组中两数和为完全平方数,则与 a 相邻的 b 和 e 必需放到 B 组,同样 c 和 d 因为分别与 b 和 e 相邻,则必需放到 A 组,但 c 与 d 相邻,即无法保证 A、B 两组中都不出现两数和为完全平方数的情形。这个命题很容易扩展到任意奇数边形的一般情形:
对于任意 n 边形,n 为大于等于 3 的奇数,没有办法把 n 个顶点分配到两个集合 A 和 B,使得该 n 边形的任意一条边的两个顶点既不同在 A 也不同在 B。
由上面的分析,可以引入奇数环的概念:k 个不同正整数组成的 k 元组 (x1, x2, ..., xk),其中 k 为大于 1 的奇数,若该 k 元组中任意两个相邻数之和为完全平方数,且首尾两数之和(即 x1 + xk)也为完全平方数,则称这个 k 元组构成一个 k 阶奇数环,简称 k数环。
于是,原题的命题的等价说法就是:
若整数 n ≥ 100,则 n, n + 1, ..., 2n 中必定存在奇数环。
拓展问题一的结论用奇数环复述起来就很直观了,即:
若 n, n + 1, ..., 2n 中存在奇数环,则这个奇数环不一定是 3 数环。
拓展问题二:若从 n 个不同的正整数中任取两个相加,所能得到的和集里至多只有两个完全平方数。请问能否把这 n 个正整数分成两组使得每组中都不存在两数之和为完全平方数?
若和集中没有完全平方数,则问题的答案显然是肯定的。
考虑和集中只有一个完全平方数,记为 s,的情形。从这 n 个数中任取两个和为 s 的数,如 u + v = s,把 u 放入 A 组,把 v 放入 B 组。此时 A = {u},B = {v}。剩余的数中如果还有两数之和为 s,如 p + q = s,同样把 p、q 分别放入 A 组和 B 组,此时 A = {u, p},B = {v, q}。在 A 组中显然有 u + p ≠ s(不然 p = v,与题设矛盾)。依此类推,直到剩余的数中不再有两数之和为 s,则把这些数全部放入 A 组。易知此情形下,问题的答案同样是肯定的。
考虑和集中恰有两个完全平方数,分别记为 s1 和 s2,的情形。从n 个数中寻找同时参与组建 s1 和 s2 的一个数,记为 u,即有 u + v = s1,u + w = s2,则把 u 放入 A 组,把 v 和 w 放入 B 组。此时 A = {u},B = {v, w},易知 v + w 既不等于 s1,也不等于 s2。把 v 和 w 加入待考察列表,依次考察列表中的数。以 v 为例:从列表中取出 v,如果未入组的数中有 x 使得 v + x = s2,则把 x 放入 v 所在组的对应组,并把 x 加入待考察列表。继续考察列表中的数,直到列表为空。
重复上面的处理过程,直到待考察列表为空且未入组的数中不再有同时参与组建 s1 和 s2 的数。此时,未入组的数中若有 p + q = s1(或 s2),则把 p 放入 A 组,q 放入 B 组。重复这个过程,直到未入组的数中不再有参与组建 s1 或 s2 的数,最后把这些数全部放入 A 组。分组完成。易知此情形下,问题的答案同样是肯定的。
综上分析,拓展问题二的答案是肯定的。
扩展问题二的结论说明:任意一个奇数环所能组建的不同完全平方数的数目一定大于 2。
拓展问题三:
(I). 求 n 的最小值,使得 n, n + 1, ..., 2n 中存在奇数环;
(II). 求 k 的最小值,使得当 n ≥ k 时,n, n + 1, ..., 2n 中存在奇数环。
前述原题的证明过程,已经求得 n = 48 时,n, n + 1, ..., 2n 中存在奇数环。接下来要考察 n < 48 时,是否还有n, n + 1, ..., 2n 中存在奇数环。同样,由原题的结论,这里第二问里的 k 满足 k ≤ 100,接下来要进一步确定 k 的最小取值。
这两个问题通过编程来求解。在下一篇里提供。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号