三个实数，其和为5，其平方和为19，求其中单个实数的最小值和最大值。
三个实数，其和为5，其平方和为19，求其中单个实数的最小值和最大值。
解法一：以 x、y、z 指代这三个实数，于是有：
x + y + z = 5 ①
x2 + y2 + z2 = 19 ②
由 ①② 组成的方程组对应于在空间直角坐标系里方程①对应的平面与方程②对应的球面所交出的一个圆。示意图如下：
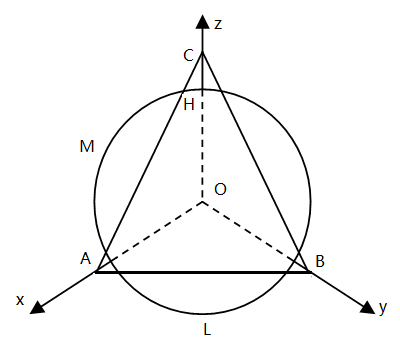
图中，OA = OB = OC = 5，A、B、C 三点确定的平面即为方程①对应的平面。圆 LMH 即为①②构成的方程组所对应的圆。其中，OH = OM = OL = 191/2，注意这里点 O 是空间直角坐标系的中心，而不是圆 LMH 的圆心。
由对称性，只需求圆 LMH 上的点在 z 轴方向坐标的最大值和最小值。在上图中可以直观地看出：
（1）点 C、H、L 在一条线上，这条线是平面 x+y+z=5 与平面 x=y 的交线；
（2）点 H 和点 C 在z 轴方向的坐标分别就是要求的最大值和最小值。
即点 H 和点 L 是圆 LMH 与平面 x=y 的两个交点。于是就有：
2x + z = 5 ③
2x2 + z2 = 19 ④
由③有 x = (5-z)/2，代入④，并经化简处理，得到：
3z2 - 10z - 13 = (3z - 13)·(z + 1) = 0
求解得 z = 13/3 或 -1，即题目中任意单个实数的最小值为 -1，最大值为 13/3。
进一步可以明确上图中点 H 的坐标为(1/3, 1/3, 13/3)，点 L 的坐标为 (3, 3, -1)。
解法二：以 x、y、z 指代这三个实数，于是有：
x + y + z = 5 ①
x2 + y2 + z2 = 19 ②
对①两端做平方操作，有：
x2 + y2 + z2 + 2(xy + yz + xz) = 25 ③
由③-②，可得 xy + yz+ xz = 3，结合①，进而可得：
xy = 3 - z(5 - z) ④
(x-y)2 = x2 + y2 - 2xy = 19 - z2 - 2(3 - z(5 - z)) = -3z2 + 10z + 13 = (-3z + 13)·(z + 1)
由于 (x-y)2 ≥ 0，于是有：
(-3z + 13)·(z + 1) ≥ 0
求解，得
-1 ≤ z ≤ 13/3
容易验证：当 x = y = 3 时，z = -1；当 x = y = 1/3 时，z = 13/3
由对称性可知，题目中任意单个实数的最小值为 -1，最大值为 13/3。
