用几何方法求解一道代数题

f(x) = (a + x²)^1/2 + [b + (c - x)²]^1/2，常数a、b、c均为正实数，x∈[0,c]。求x为何值时 f(x) 取得最小值。

解：构造如下图所示几何图形：

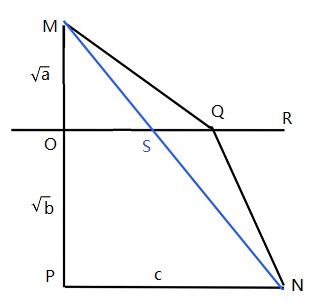
其中MP⊥OR，OR // PN，OM=a^1/2，OP=b^1/2，OR=PN=c，Q是OR上动点，OQ=x

由勾股定理易知，MQ = (a + x²)^1/2，QN = [b + (c - x)²]^1/2 

于是f(x) = MQ + QN，问题等价于考察动点Q在OR上的什么位置会让MQ+QN取得最小值

由两点间直线段最短可知，当Q在MN与OR的交点S的位置，MQ+QN取最小值。接下来要求出OS

由MO:OS = MP:PN，有

OS = MO·PN / MP = a^1/2·c / (a^1/2 + b^1/2)

即当x = a^1/2·c / (a^1/2 + b^1/2)时，f(x)取得最小值。

附言：

周末看了人教版初二上册数学教材里的13.4节（课题学习：最短路径问题），一番思考，遂有此题。

 拓展题：f(x) = (a + x²)^1/2 + [b + (c - x)²]^1/2，常数a、b、c均为正实数，x∈R。试判断 f(x) 的单调情况。

 分析：在上图中动点Q由点S向左侧平移时，可以很直观地发现三角形QMN的面积会逐渐变大（新三角形会完全覆盖旧三角形）；同样，动点Q由点S向右平移时，三角形QMN的面积也会逐渐变大（新三角形会完全覆盖旧三角形）。因此大致可以猜测f(x)在点S左侧单调递减，在点S右侧单调递增，且只有点S这一处拐点。注意这里的x可为任意实数，即动点Q不再局限于在点O与点R之间移动，而是可以在OR所在的整条直线上移动。

引理：在三角形ABC的底边AB上任取一点D，连接DC并延长至三角形ABC外一点E，连接EA和EB. 则有EA+EB > CA+CB.

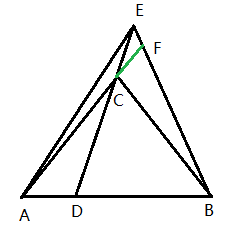
证明：若点D取在点A或点B，结论显然成立。不妨以点D取在点A为例，此时EA=EC+CA，由EC+EB > CB，知EA+EB=CA+EC+EB > CA+CB.

若点D不取在点A或点B位置，延长AC交BE于点F，于是有

EA+EB = EA+EF+FB > FA+FB = FC+CA+FB > CA+CB.

引理证明完毕。

由这个引理可知上述判断正确。记g=a^1/2·c / (a^1/2 + b^1/2)，则f(x)在(-∞, g]上单调递减，在[g, +∞)上单调递增。