一道心形数独题的求解

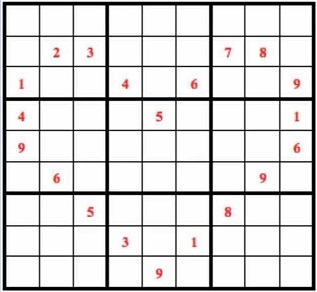
解：约定几个简记符号：用(a,b)=c表示第a行第b列的位置上的数为c；用[a]表示第a行；用{a}表示第a列。

①考虑[2]：

由上中宫第三行的4和6，可知[2]的中间三格不能为4和6，即4和6只能填置于两侧的空缺位置；再由{1}有4及{9}有6，可知(2,1)=6及(2,9)=4。

中间剩余三格待填数字为1、5、9，由于{5}已经有5和9，于是(2,5)=1。如下图所示：

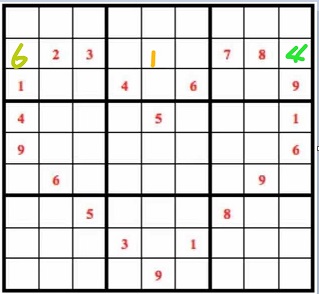
 ②考虑[4]和[2]：

由于中左宫和中右宫都有6和9，可知[4]里的6和9只能填到(4,4)和(4,6)；再由{6}里已经有6，可知(4,6)=9及(4,4)=6。

再考虑[2]，易知(2,4)=9及(2,6)=5。如下图所示：

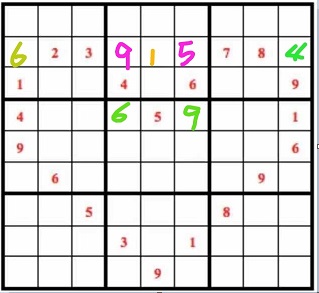
 ③填放9、8、4：

考虑{7}，由上右宫和中右宫都有9，且[9]里也有9，可知(8,7)=9。同样考虑{9}，由上右宫和下右宫都有8，可知(6,9)=8。考虑[7]，同样易知(7,2)=9。

考虑{3}，其空缺的格除了第一行之外，其余所有行里都有9，于是(1,3)=9。

考虑上左宫，由[3]和{1}里都有有4，可知(1,2)=4。如下图所示：

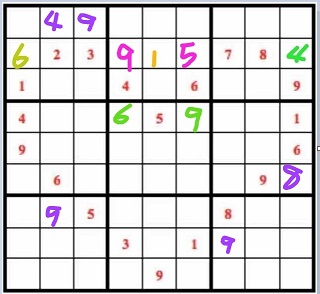
 ④填放1、6、5、4：

考虑[7]，由下中宫有1且{1}和{9}都有1，可知(7,8)=1。再考虑{7}，由中右宫和下右宫以及[3]都有1，可知(1,7)=1。

考虑左下宫，由左上宫和左中宫都有4和6，可以推知{3}里的4和6只能填到(8,3)和(9,3)两个位置；再由{1}和[8]里都有1，可知(9,2)=1。

考虑{7}，由右中宫和[3]都有6，可知(9,7)=6。于是又可以明确(9,3)=4及(8,3)=6。

考虑右上宫，由[3]和{9}都有6，可知(1,8)=6。

考虑{4}，由上中宫和中心宫以及[7]里都有5，可知(9,4)=5。如下图所示：

⑤把6、5、4填完：

考虑下中宫里的6，由[8]、[9]、{4}和{6}里都有6，知(7,5)=6；同样考虑下中宫里的4，易知(7,6)=4。

考虑右下宫，由[9]和{9}都有4，知(8,8)=4；再由[7]和[9]都有5，知(8,9)=5。

考虑[1]里的5，易知(1,1)=5；再考虑[6]里的5，由中心宫以及{1}和{3}里都有5，知(6,7)=5；进而易知，右上宫里(3,8)=5，以及左中宫里(5,2)=5。

类似方法可把4填充完整。如下图所示：

 ⑥最后的突破：

考虑{2}里的3，由左上宫和[8]里都有3，可知(4,2)=3。再往后按上述方法可以推定出所有待定位置上的数。最终得到如下图所示的一个解：

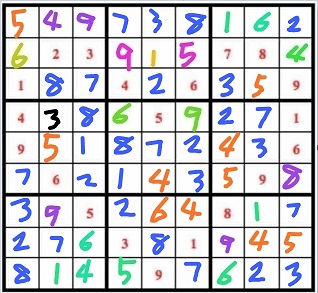
 检查两条大对角线，存在重复的数，说明这个解不是严格的对角线数独的解。