对20个正三角形顶点染色问题的分析与求解
下图中有三种正三角形，边长分别为1、2和3；这些三角形共有13个顶点，现要把每个顶点染成红色或蓝色，要求图中每个连出的三角形的三个顶点不能完全同色。求有多少种染色方案。
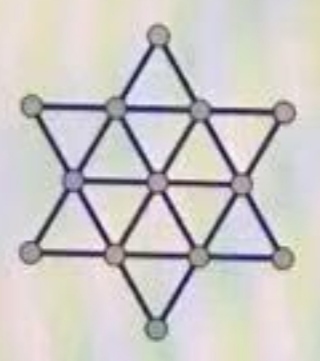
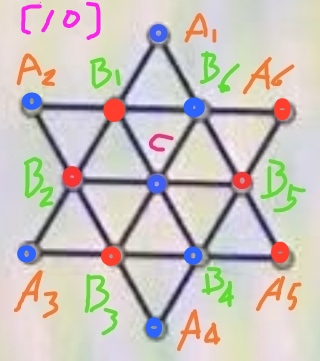
分析：为方便说明，对图中的顶点做下图所示的字母标记。由对称性可知，这13个顶点分为三类，外层的6个A类顶点、内层的6个B类顶点和处在中心位置的C（记为中央C）。
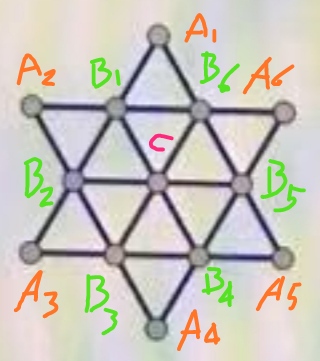
中央C只和B类顶点构成6个边长为1的正三角形（简记为小三角形，边长为2和3的正三角形则分别记为中三角形和大三角形）；6个B类顶点构成一个正六边形，每个B类点和相邻的5个点（两个A类点、两个B类点以及中央C）构成4个小三角形，另外，每个B类点还参与构成两个中三角形；每个A类点参与构成小、中、大三角形各一个。
另外，中三角形每条边上的三个顶点（即两个端点及它们的中点）不能染成同一个颜色（如A3、B3、B4都为红色，则B1、B2、C都只能为蓝色，而这三个蓝色顶点构成一个小三角形，不符合染色要求）。这个特征可以用来加快解题速度。
解法一：（walls老师提供了本题及一个可行解法，这里沿用该解法的选点策略）
步骤1、先对大三角形A1A3A5的三个顶点进行染色，共有2^3-2=6种染法，每种都是两个顶点同色并和第三个顶点异色，由对称性知，只需考察其中一种情形，得到全体顶点的染法种数，再乘以6便得到题解所求种数。以下以图（1）所示的情形作进一步考察：
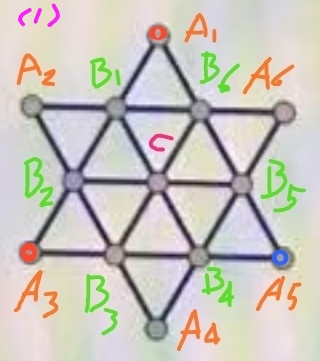
在图（1）中，由已染色的三个顶点并不能推定其余任何一点的染色情况，因此还需要选更多的点分步骤考察。
步骤2、选取点B5，将其染成红色，并进一步推定其它点的染色情况，得到图（2）：
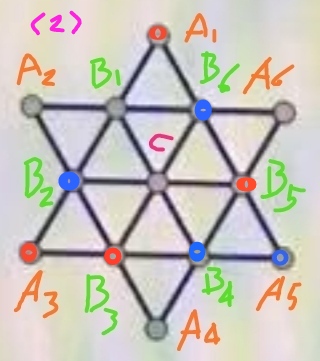
此时剩下5个颜色不能推定的点。
步骤3、选取点B1，将其染成蓝色，并进一步推定其它剩余点的颜色，得到图（3）所示的满足题设要求的一种染色方案：
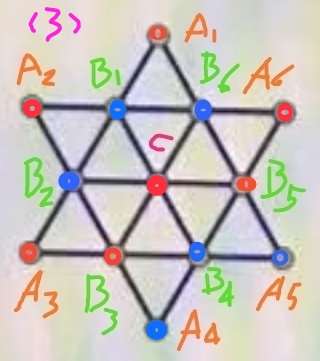
步骤4、回到图（2）的情形，将B1染成红色，得到图（4）：
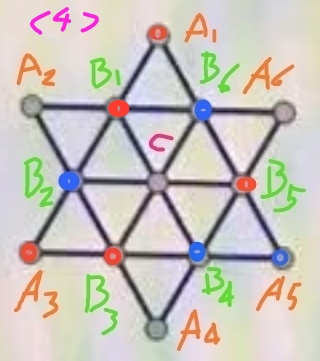
这时有4个点不能推定颜色，分别是三个A类点和中央C。由于点C不和A类点构成三角形，因而图（4）的情形对应有(2^3-2)*2=12种满足要求的染色方案。这说明图（2）的情形对应有12+1=13种满足要求的染色方案。
步骤5、回到图（1），将B5染成蓝色，并进一步推定其它点的颜色，得到图（5）：
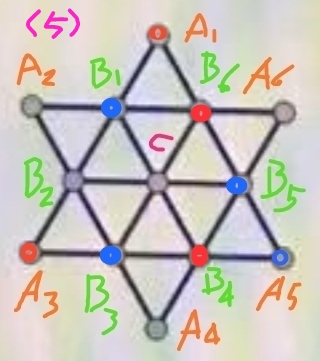
步骤6、选取B2，染成红色，得到类似图（4）的情形，同样对应有12种满足要求的染色方案。
步骤7、回到图（5），把B2染成蓝色，并进一步推定其它点的颜色，得到图（6）所示的一种满足要求的染色方案：
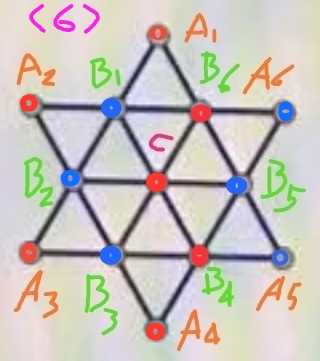
这说明，图（1）在B5染成蓝色的情形下有12+1=13种满足要求的染色方案。因此图（1）的情形对应有13+13=26种满足要求的染色方案。于是所求的染色方案共有26*6=156种。
解法二：从考察一个中三角形的三个顶点染色情况入手。
步骤1、选取中三角形A1B2B5，将其三个顶点按图[1]所示进行染色：
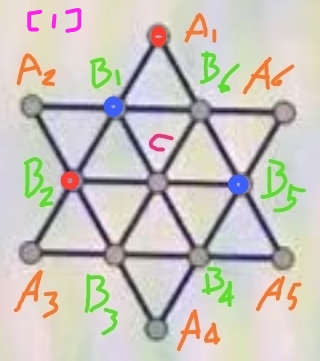
图[1]中A1和B2都是红色，所以可以推定B1为蓝色。
步骤2、选取顶点A3，将其染成红色，并推定其它点的颜色，得到图[2]：
图[2]对应有(2^3-2)*2=12种满足要求的染色方案。
步骤3、回到图[1]，将A3染成蓝色，并推定其它点的颜色，得到图[3]：
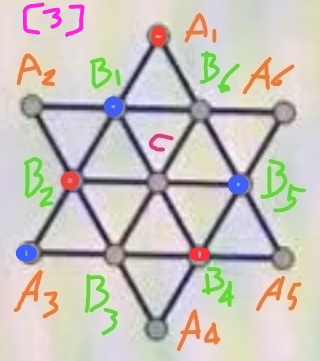
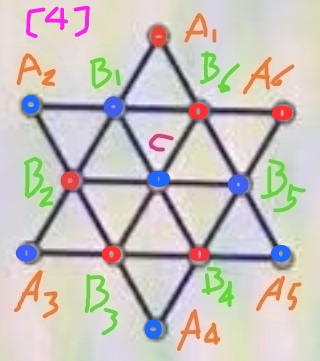
步骤4、选取顶点B3，将其染成红色，推定其它点的颜色，得到图[4]所示的满足要求的一种染色方案：
步骤5、回到图[3]，将B3染成蓝色，得到图[5]：
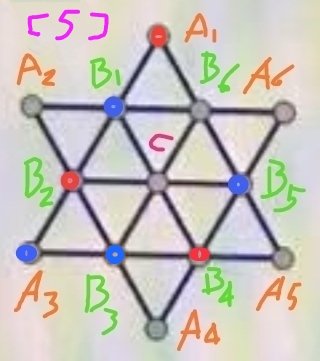
这时仍有6个点的颜色不能推定。
步骤6、选取B6，将其染成红色，得到图[6]：
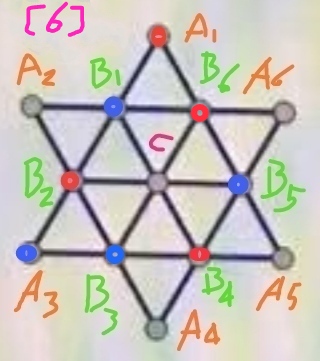
图[6]中未染色的5个点可以分成相对独立的三部分：顶点A5；中央C；A2、A4、A6。于是图[6]的情形对应2*2*6=24种满足要求的染色方案。
步骤7、回到图[5]，将B6染成蓝色，并推定其它点的颜色，得到图[7]所示的一种满足要求的染色方案：
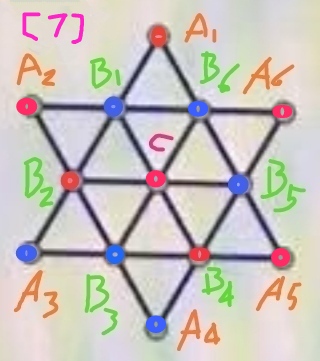
综上可知，图[1]的情形对应有12+1+24+1=38种满足要求的染色方案。但此时不能由38乘上6求全体染色方案的种数，因为中三角形A1B2B5在整体对称性上不如解法一里的大三角形A1A3A5。一个中三角形是一个A类点搭配两个B类点；其中，两个B类点同色的情形（对应的中三角形有两种染法）满足一种整体对称性，两个B类点异色的情形（对应的中三角形有4种染法）满足另一种整体对称性。
步骤8、考察图[8]所示的情形：
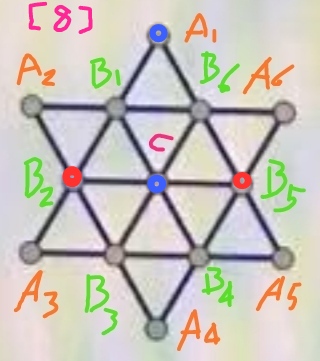
这里中央C为蓝色是由B2和B5都是红色而推定的。
步骤9、选取A3，将其染成红色，推定其它点的颜色，得到图[9]所示的一种满足要求的染色方案：
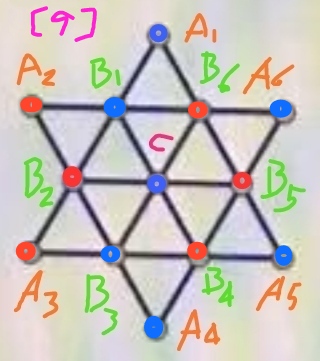
步骤10、回到图[8]，将A3染成蓝色，并推定其它点的颜色，得到图[10]所示的一种满足要求的染色方案：
综上，所求的全体染色方案共有38*4+(1+1)*2=156种。
附言：
本题还可以从考察一组共线点的染色情形入手进行求解，比如选取A2、B1、B6、A6这四个点，它们可能的染色情形有6种，即[红红蓝蓝]、[蓝蓝红红]、[红蓝红蓝]、[蓝红蓝红]、[红蓝蓝红]、[蓝红红蓝]，按对称性可分为三组，每组选取一种分步骤考察。从整体对称性来看，由一个大三角形的三个顶点入手是最优求解方法。
