24点游戏（24 game）的C++编程求解实现

什么是24点游戏

24点游戏，英文叫做24 game，是对给定的4个非负整数进行加减乘除运算，要求每个数都要被用到且仅用到一次，并得到最终的运算结果为24。比如3、8、3、8这四个数，可以找出唯一的一个解是8/(3-8/3)。

本程序的实现特点

1、采用降阶法实现，不再局限于输入4个数，也不局限于求值为24。

2、仅用整数运算，而不用浮点运算。

3、求解去重处理。

关于求解去重

24点游戏的编程求解的基本思路本质上就是遍历的思路，把每种运算组合都计算出其结果，所有最终结果为24的运算组合就是全体的解。但是单纯遍历出来的解往往会有大量的重复解。比如用1、2、3、4这四个数求24，1*2*3*4是一个解，按乘法交换律和结合律由这个解可以衍生出很多类似的解，如：2*1*3*4，1*2*(3*4)，1*(2*3)*4，2*3*4*1，2*3*4/1，等等。还有很多其它类型的重复解。后面再细说。总的来说，对求解做去重处理是为了尽快求解并简洁地展现出来。本程序相当比重的设计和逻辑实现都是用于应对去重这个任务的。

基础数据结构设计

SFraction

 1 struct SFraction
 2 {
 3     u64 numerator;
 4     u64 denominator;
 5     bool bNegative;
 6 
 7     SFraction()
 8     {
 9         reset();
10     }
11     void reset()
12     {
13         numerator = 0;
14         denominator = 1;
15         bNegative = false;
16     }
17     void setValue(u32 uiVal)
18     {
19         numerator = (u64)uiVal;
20         denominator = 1;
21         bNegative = false;
22     }
23     bool isZero() const
24     {
25         return (numerator == 0);
26     }
27     bool isOne() const
28     {
29         return (numerator != 0 && !bNegative && numerator == denominator);
30     }
31     bool operator==(const SFraction& oVal) const
32     {
33         SFraction oResult = fractAdd(*this, minusByZero(oVal));
34         return (oResult.numerator == 0);
35     }
36     bool operator<(const SFraction& oVal) const
37     {
38         SFraction oResult = fractAdd(*this, minusByZero(oVal));
39         return (oResult.numerator != 0 && oResult.bNegative);
40     }
41     bool operator>(const SFraction& oVal) const
42     {
43         SFraction oResult = fractAdd(*this, minusByZero(oVal));
44         return (oResult.numerator != 0 && !oResult.bNegative);
45     }
46 };

这里，表示分数的数据结构 SFraction 沿用了用C++实现的有理数（分数）四则混合运算计算器里的定义，相应增加了本程序需要的 isZero、isOne、operator==、operator<、operator> 等方法。分数加法函数 fractAdd、分数乘法函数 fractMultiply、求相反数、求倒数以及求最大公约数、最小公倍数等辅助函数全部沿用用C++实现的有理数（分数）四则混合运算计算器里的定义和实现。

EnumOp

enum EnumOp{E_OP_NONE, E_OP_ADD, E_OP_R_SUBST, E_OP_MULTIPLE, E_OP_DIVIDE, E_OP_R_DIVIDE};

EnumOp 定义了5种二元运算符：加、反减、乘、除、反除。

对于除法运算，这里设置了两个运算符，是基于两个因素的考虑：

（1）a / b 通常并不等于 b / a。

（2）为了方便去重处理，本程序内部表达运算数 a 和 b 的二元运算时，总是把值小的数放在左边，值大的数放在右边。即：左数 <= 右数。

假设 a 小于 b，那么有如下对应关系：

（1）a + b 和 b + a 都对应 a 加 b

（2）b - a 对应 a 反减 b

（3）a * b 和 b * a 都对应 a 乘 b

（4）b / a 对应 a 除 b

（5）a / b 对应 a 反除 b

这里的反除就是数学中的称谓“除以”。另外还需要说明一下：减法运算为什么不设置两个运算符，即只需考虑大值减小值的情形，而忽略小值减大值出现负数的情形。这是因为参与运算的原始输入数值限定为非负整数，而最终要求得到的运算结果也是一个非负整数。

用几个例子说明：

以1、3、26 求 24 为例，1-3+26 是一个解，即 -2 加上 26 得 24，但是这种情形总有对应的大值减小值的解，即 26-(3-1)，就是说一个负数加一个大正数等于这个大正数减去负数的相反数。

类似地，考虑由1、3、22 求 24，那么 22-(1-3) 是一个解，但对这个解稍作变形就得到不会出现负数的解，即 22+(3-1)。

另外两个负数相乘或相除得到一个正数的情形，同样有对应的避免出现负数的变形，比如 (1-3)*(7-19) 可变形为 (3-1)*(19-7)，(7-10)*(1/(30-38)) 可变形为 (10-7)*(1/(38-30)) 。

EnumOp 还定义了用于表示没有二元运算的符号 E_OP_NONE，其作用随后就会看到。

SExpress

 1 struct SExpress
 2 {
 3     SFraction oVal;
 4     std::string strExpress;
 5     EnumOp eOp;
 6     SFraction oL, oR;
 7 
 8     SExpress()
 9     {
10         eOp = E_OP_NONE;
11     }
12 };

SExpress 是一个表达式的表示结构，且有如下语义：

1、每个参与二元运算的原始输入数值，都是一个叶子表达式，分量 SFraction oVal 是表达式自身的数值，其 EnumOp eOp 分量取值为 E_OP_NONE，以标定该表达式节点为叶子节点

2、对两个叶子表达式（记为 a 和 b）施予前述的某一个二元运算符（记为 ~）可以得到一个新的表达式（记为 N），这个新的表达式的 SFraction oL, oR 分量分别记录两个参与运算的表达式的数值，且满足 oL <= oR；新表达式的 EnumOp eOp 分量则记录对应的二元运算符。可以概述为 a 和 b 按 ~ 聚合得到 N，对应的纯符号表示式为：a~b=N

3、对任意两个表达式施予前述的某一个二元运算符可以得到一个新的表达式，这个过程称作一次聚合（0 作除数的情形除外）

4、为区别于叶子表达式，由聚合得到的新表达式统称为枝表达式

5、所有给定的叶子表达式都参与且仅参与一次聚合，以及中间产生的枝表达式也都参与且仅参与一次聚合，最终总会得到一个根表达式

6、分量 std::string strExpress 以字符串形式记录对应的表达式是如何由叶子表达式聚合而成的

本程序的核心任务可以表达为：对所有给定的叶子表达式，遍历出各种聚合序列，对每种聚合序列得到的根表达式求值，判断是否和指定的值相等。

主函数实现

 1 int main(int argc, char* argv[])
 2 {
 3     printf(" 24 game pro version 1.0 by Read Alps\n\n");
 4     printf(" Please input the target non-negative integer to make [default 24]:");
 5     std::string strInput;
 6     getline(std::cin, strInput);
 7     u32 uiVal = 0;
 8     if (!shiftToU32(strInput, uiVal))
 9     {
10         printf(" Invalid input; use 24 instead.\n");
11         uiVal = 24;
12     }
13     CBackwardCalcor::sm_oAnswer.setValue(uiVal);
14 
15     CLog::instance();
16     printf(" Do you want to log details in workflow.log? [y/n, default n]:");
17     getline(std::cin, strInput);
18     if (strInput == "y")
19     {
20         CLog::instance()->setLogPathAndName(getMainPath().c_str(), "workflow.log");
21         CLog::instance()->setLogLevel(LOG_DBG);
22     }
23 
24     while (true)
25     {
26         CBackwardCalcor::sm_setResult.clear();
27         printf("\n Please input several (at most 6) non-negative integers separated by comma to make %u or q to quit:", uiVal);
28         getline(std::cin, strInput);
29         trimString(strInput);
30         if (strInput == "q")
31             break;
32         std::vector<std::string> vecStr;
33         if (std::string::npos != strInput.find(","))
34             divideString2Vec(strInput, ",", vecStr);
35         if (isIntStrVec(vecStr) == 0)
36         {
37             printf(" Invalid input.\n\n");
38             continue;
39         }
40         if (vecStr.size() > 6)
41         {
42             printf("At most 6 integers.\n");
43             continue;
44         }
45         u32 uiStart = (u32)GetTickCount();
46         CBackwardCalcor oCalc(vecStr);
47         oCalc.exec();
48         if (CBackwardCalcor::sm_setResult.empty())
49         {
50             printf(" From %s, there is no solution to make %u by using +-*/ and ().\n", strInput.c_str(), uiVal);
51             printf(" Used time(ms): %u.\n", GetTickCount() - uiStart);
52             continue;
53         }
54         int nCount = 1;
55         for (std::set<std::string>::const_iterator it = CBackwardCalcor::sm_setResult.begin(); it != CBackwardCalcor::sm_setResult.end(); ++it)
56             printf(" %d. %s\n", nCount++, it->c_str());
57         printf(" Used time(ms): %u.\n", GetTickCount() - uiStart);
58     } // end of main loop
59     printf("\n");
60     return 0;
61 }

main 函数实现一个交互式console程序，进入主循环之前有两次交互输入，指定要计算的目标数值以及是否记录详细日志。

进入到主循环里，让输入一组逗号隔开的非负整数，随后的如下语句是把输入的字符串分解到一个数字字符串动态数组里：

32         std::vector<std::string> vecStr;
33         if (std::string::npos != strInput.find(","))
34             divideString2Vec(strInput, ",", vecStr);

然后以这个动态数组为参数实例化一个 CBackwardCalcor 对象，并调用该对象的 exec 方法进行求解，最后输出求解结果，重新开始循环。

Linux下运行示例

[root@localhost bin]# ./24GamePro
24 game pro version 1.0 by Read Alps

Please input the target non-negative integer to make [default 24]:
Do you want to log details in workflow.log? [y/n, default n]:

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:3,4,5,6
1. (3+5-4)*6
Used time(ms): 2.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:1,2,3,4
1. (1+3)*(2+4)
2. 1*2*3*4
3. 4*(1+2+3)
Used time(ms): 1.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:8,3,8,3
1. 8/(3-8/3)
Used time(ms): 0.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:56,67,78,89
From 56,67,78,89, there is no solution to make 24 by using +-*/ and ().
Used time(ms): 2.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:23,45,67,89,34
1. (23+45)/34+89-67
Used time(ms): 62.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:23,45,67,89,34,66
1. (23+45-66)*(34+67-89)
2. (89-67)*45/(34-23)-66
3. 23+34-66*67/(45+89)
4. 23+45*66/(67-34)-89
5. 66/(45+89)+34/67+23
6. 67+89-66*(23+45)/34
Used time(ms): 3018.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:q

[root@localhost bin]#

CBackwardCalcor 类接口与成员

 1 class CBackwardCalcor
 2 {
 3 public:
 4     CBackwardCalcor(const std::vector<std::string>& vecStr);
 5     CBackwardCalcor(const std::vector<SExpress>& vecExp);
 6     void exec();
 7 
 8 private:
 9     void workOnLevel(size_t seq1, size_t seq2);
10     void stepOver(size_t& seq1, size_t& seq2);
11     void reduct(EnumOp eOp, size_t seq1, size_t seq2, const std::vector<SExpress>& vecLeft);
12     void doBiOp(EnumOp eOp, const SExpress& oExp1, const SExpress& oExp2, SExpress& oReduct, bool bNoLeft);
13     bool isRedundant(EnumOp eOpL, EnumOp eOpR, EnumOp eOp);
14     bool isRedundantEx(const SExpress& oExp1, const SExpress& oExp2, EnumOp eOp);
15 
16     void setAscendingOrder();
17     bool higherLevel(size_t seq1, size_t seq2);
18     bool topLevel(size_t seq1, size_t seq2);
19 
20     std::vector<SExpress> m_vecExpress;
21 
22     /// 头两个参与运算的数作为当前水位
23     SFraction m_oCurValL; // 左数
24     SFraction m_oCurValR; // 右数
25 
26 public:
27     static SFraction sm_oAnswer;
28     static std::set<std::string> sm_setResult;
29 
30 private:
31     CBackwardCalcor(){};
32 };

CBackwardCalcor 类里有两个静态分量：sm_oAnswer 和 sm_setResult，前者存放交互指定的要计算的目标数值，后者存放求解的集合。

CBackwardCalcor 类的两个构造函数

 1 CBackwardCalcor::CBackwardCalcor(const std::vector<std::string>& vecStr)
 2 {
 3     SExpress oExp;
 4     for (size_t idx = 0; idx < vecStr.size(); idx++)
 5     {
 6         oExp.oVal.setValue(strtoul(vecStr[idx].c_str(), 0, 10));
 7         oExp.strExpress = vecStr[idx];
 8         m_vecExpress.push_back(oExp);
 9     }
10 }
11 
12 CBackwardCalcor::CBackwardCalcor(const std::vector<SExpress>& vecExp)
13 {
14     m_vecExpress = vecExp;
15 }

main 函数里的 CBackwardCalcor oCalc(vecStr) 语句实例化一个 CBackwardCalcor 对象，并调用第一个构造函数把输入的一组字符串数值转化为一组叶子表达式，存放到成员 m_vecExpress 里。

第二个构造函数后面会用到。

CBackwardCalcor::exec 接口实现

 1 void CBackwardCalcor::exec()
 2 {
 3     setAscendingOrder();
 4 
 5     if (CLog::instance()->meetLogCond(LOG_DBG))
 6     {
 7         std::string str = "Dealing:";
 8         for (size_t idx = 0; idx < m_vecExpress.size(); idx++)
 9             str += (" " + m_vecExpress[idx].strExpress);
10         CLog::LogMsgS(LOG_DBG, str.c_str());
11     }
12 
13     if (m_vecExpress.size() == 1)
14     {
15         if (m_vecExpress[0].oVal == sm_oAnswer)
16             sm_setResult.insert(m_vecExpress[0].strExpress);
17         return;
18     }
19     if (sm_oAnswer.isZero() && m_vecExpress[m_vecExpress.size() - 1].oVal.isZero())
20     {
21         std::string str = "0";
22         for (size_t idx = 1; idx < m_vecExpress.size(); idx++)
23             str += "+0";
24         sm_setResult.insert(str);
25         return;
26     }
27 
28     size_t seq1 = 0, seq2 = 1;
29     while (seq1 + 1 < m_vecExpress.size())
30     {
31         if (higherLevel(seq1, seq2))
32         {
33             m_oCurValL = m_vecExpress[seq1].oVal;
34             m_oCurValR = m_vecExpress[seq2].oVal;
35             workOnLevel(seq1, seq2);
36             if (topLevel(seq1, seq2))
37                 break;
38         }
39         stepOver(seq1, seq2);
40     }
41 }

CBackwardCalcor::exec 的实现代码分为四个部分。第一部分是调用 setAscendingOrder 接口对 m_vecExpress 里的表达式按数值从小到大进行排序。

setAscendingOrder 接口的实现代码如下：

 1 void CBackwardCalcor::setAscendingOrder()
 2 {
 3     for (size_t idx = 1; idx < m_vecExpress.size(); idx++){
 4         for (size_t preidx = 0; preidx < idx; preidx++){
 5             if (m_vecExpress[idx].oVal < m_vecExpress[preidx].oVal){
 6                 SExpress oLow = m_vecExpress[idx];
 7                 for (size_t mvidx = idx; mvidx > preidx; --mvidx)
 8                     m_vecExpress[mvidx] = m_vecExpress[mvidx - 1];
 9                 m_vecExpress[preidx] = oLow;
10             }
11         }
12     }
13 }

CBackwardCalcor::exec 实现代码的第二部分是记录日志。

第三部分是对两种特殊情形的处理：

1、输入参与运算的数值只有一个的情形，直接判断该数值和指定要计算的目标数值是否相等即可完成求解。

2、由若干个0求0的情形，只取连加形式的一种解。

其实第二种情形有很多种解，比如等式 0+0+0+0=0，其中任意一个加号可以换成减号或乘号，依然会保持等式成立。但鉴于数值 0 的特殊性，本程序只取连加形式的一种解，其它解都当作重复解而不予展示。

第四部分代码是 exec 接口的主体逻辑实现，以下结合一个示例进行阐述。

示例：由 2、2、2、3四个数求 24。

（1）取第一和第二两个数，即2和2

　　a）做加法运算，得到4，接下来降阶成由4、2、3求24

　　b）做减法运算，得到0，接下来降阶成由0、2、3求24

　　c）做乘法运算，得到4，接下来降阶成由4、2、3求24

　　d）做除法运算，得到1，接下来降阶成由1、2、3求24

　　e）做反除法运算，得到1，接下来降阶成由1、2、3求24

（2）取第一和第三两个数，即2和2

　　a）做加法运算，得到4，接下来降阶成由4、2、3求24

　　b）做减法运算，得到0，接下来降阶成由0、2、3求24

　　c）做乘法运算，得到4，接下来降阶成由4、2、3求24

　　d）做除法运算，得到1，接下来降阶成由1、2、3求24

　　e）做反除法运算，得到1，接下来降阶成由1、2、3求24

（3）取第一和第四两个数，即2和3

　　a）做加法运算，得到5，接下来降阶成由5、2、3求24

　　b）做减法运算，得到1，接下来降阶成由1、2、2求24

　　c）做乘法运算，得到6，接下来降阶成由6、2、2求24

　　d）做除法运算，得到3/2，接下来降阶成由3/2、2、2求24

　　e）做反除法运算，得到2/3，接下来降阶成由2/3、2、2求24

再往后，还有：

（4）取第二和第三两个数，即2和2

（5）取第二和第四两个数，即2和3

（6）取第三和第四两个数，即2和3

照这样遍历下来，确实可以确保把所有的解求出来。但是，从过程看，很多步骤完全是多余的，比如（2）完全和（1）重复；（4）和（1）重复；（5）、（6）和（3）重复。

现在来看 CBackwardCalcor::exec 的第四部分代码是如何实现上述求解逻辑并避免上述重复步骤的：

28     size_t seq1 = 0, seq2 = 1;
29     while (seq1 + 1 < m_vecExpress.size())
30     {
31         if (higherLevel(seq1, seq2))
32         {
33             m_oCurValL = m_vecExpress[seq1].oVal;
34             m_oCurValR = m_vecExpress[seq2].oVal;
35             workOnLevel(seq1, seq2);
36             if (topLevel(seq1, seq2))
37                 break;
38         }
39         stepOver(seq1, seq2);
40     }

两个局部变量 seq1 和 seq2 分别记录首先参与聚合运算的左右两个表达式在表达式数组里所对应的下标，初始值分别为 0 和 1，即考虑让数值最小的两个表达式先做聚合运算的情形；while 循环体内有对这两个下标变量做步进处理的接口，该接口实现如下：

 1 void CBackwardCalcor::stepOver(size_t& seq1, size_t& seq2)
 2 {
 3     if (seq2 + 1 < m_vecExpress.size())
 4     {
 5         ++seq2;
 6         return;
 7     }
 8     ++seq1;
 9     seq2 = seq1 + 1;
10 }

但正如上述示例所示，单是对这两个下标变量做步进遍历可能会碰到很多完全多余的运算。为解决这个问题，在 CBackwardCalcor 里引入了两个水位成员：

    /// 头两个参与运算的数作为当前水位
    SFraction m_oCurValL; // 左数
    SFraction m_oCurValR; // 右数

水位就是一个有序值对，而求解的过程则按水位由低到高的总体趋势被分解成若干个子过程。上述示例里，子过程（1）的水位是(2,2)；子过程（2）的水位还是(2,2)；子过程（3）的水位是(2,3)；子过程（4）的水位是(2,2)；子过程（5）和（6）的水位都是(2,3)。由这个示例可以看到，在步进过程中，水位有可能由高变低，但总体趋势是由低到高的。

CBackwardCalcor 实例化一个对象时，其分量m_oCurValL 和 m_oCurValR 都被初始化为数值0，就是说初始设定的水位是(0,0)。higherLevel 接口的实现如下：

1 bool CBackwardCalcor::higherLevel(size_t seq1, size_t seq2)
2 {
3     return (m_vecExpress[seq1].oVal > m_oCurValL ? true : m_vecExpress[seq2].oVal > m_oCurValR);
4 }

if (higherLevel(seq1, seq2))条件体内的那几行代码的逻辑是：更新当前水位；调用 workOnLevel 接口在当前水位进行求解；判断当前水位是否为最高水位，是则退出循环，求解完成。概言之：只有水位升高时 workOnLevel 接口才会被调用。上述示例中的6个子过程，只有（1）和（3）会被执行，其它的都被当成重复过程直接跳过。

topLevel 接口的实现如下：

1 bool CBackwardCalcor::topLevel(size_t seq1, size_t seq2)
2 {
3     size_t total = m_vecExpress.size();
4     return (m_vecExpress[seq1].oVal == m_vecExpress[total - 2].oVal && m_vecExpress[seq2].oVal == m_vecExpress[total - 1].oVal);
5 }

所谓最高水位，就是输入的一组数值经由小到大排序后排在最后的两个数值构成的有序值对。

这里还有一个疑问需要消除：因为限定了只能输入非负整数，所能输入的一组数值的最低水位是(0,0)，而一个CBackwardCalcor 对象实例化的初始水位就是(0,0)，而且只有水位升高时 workOnLevel 接口才会被调用，那么由 0、0、3、8求24，水位(0,0)对应的子过程会被当成重复过程跳过，这样是否合理？

为说明这么处理是合理的，考察一般性的情形，即由 0、0、k1、k2、……、kn 这 n+2 个非负整数求非负整数 k 的情形。0 和 0 做加减乘（除非法）的二元聚合运算，只能得到 0，说明所考察的情形等价于由 0、k1、k2、……、kn 这 n+1 个非负整数求非负整数 k 的情形。任取后者的一个解，记为 [...] = k，[...] 为一个复合表达式，从结构上而言是以 0、k1、k2、……、kn 这 n+1 个数为叶子节点的一棵二叉树。对这个二叉树的根和新添的叶子节点 0 做加法运算，就得到一棵新的二叉树，它以0、0、k1、k2、……、kn 这 n+2 个数为叶子节点。就是说，[...] + 0 = k 是所考察情形的一个解。

上述结论说明，当水位为 (0,0) 时，跳过这个水位对应的子过程是合理的，因为每个带有0与0聚合的解都会有对应的不带0与0聚合的解。例如：0+0+3*8 = 0+(0+3*8)。

当然有一种情况是例外的，即一般情形中 k1=k2=...=kn=k=0，即由 n+2 个 0 求 0 的情形，其最低水位和最高水位都是 (0,0)，就是说求求解过程只有一个子过程，直接跳过这个子过程，就会误判为无解。所以在 exec 接口的代码实现的第二部分提前应对了这种例外情况。

CBackwardCalcor::workOnLevel 接口实现

workOnLevel 的实现分为三部分，具体如下：

 1 void CBackwardCalcor::workOnLevel(size_t seq1, size_t seq2)
 2 {
 3     std::vector<SExpress> vecLeft;
 4     for (size_t idx = 0; idx < m_vecExpress.size(); ++idx)
 5     {
 6         if (idx != seq1 && idx != seq2)
 7             vecLeft.push_back(m_vecExpress[idx]);
 8     }
 9 
10     if (CLog::instance()->meetLogCond(LOG_DBG))
11     {
12         std::string str = "no pending nodes";
13         if (!vecLeft.empty())
14         {
15             str = u32ToStr(vecLeft.size()) + " pending node(s):";
16             for (size_t idx = 0; idx < vecLeft.size(); idx++)
17                 str += (" " + vecLeft[idx].strExpress);
18         }
19         CLog::LogMsg(LOG_DBG, "cur two: L=%s, R=%s with %s", m_vecExpress[seq1].strExpress.c_str(), m_vecExpress[seq2].strExpress.c_str(), str.c_str());
20     }
21 
22     reduct(E_OP_ADD, seq1, seq2, vecLeft);
23     reduct(E_OP_MULTIPLE, seq1, seq2, vecLeft);
24     reduct(E_OP_R_SUBST, seq1, seq2, vecLeft);
25     reduct( E_OP_DIVIDE, seq1, seq2, vecLeft);
26     reduct(E_OP_R_DIVIDE, seq1, seq2, vecLeft);
27 }

第一部分是由 m_vecExpress组建一个新的动态数组 vecLeft，存放当前水位下首先参与聚合运算的两个表达式之外的其余表达式，这个数组称作剩余表达式数组。

第二部分是记日志。

第三部分是按二元运算可能的运算符逐个去调用聚合接口 reduct。这里的5个 reduct 调用正好对应前述示例中的5个子子过程：a）、b）、c）、d）、e）。

为清晰起见，把对整体求解过程中按水位划分出的一级子过程简称为水位子过程，用（1）、（2）、……等标记；而把在一个水位子进程内部按当前水位的左数和右数的不同聚合方式又划分出的5个二级子过程简称为聚合子过程，用a）、b）、……等标记。

运算去重策略细则

本程序实现的去重策略主要包括两大类：一类是水位去重策略，上面已有详细阐述；另一类是运算去重策略，这一类又可概括为如下两个子类（以下说明均假设 a、b、c、d、p、q、r 为非负整数，且满足 p <= q），各有若干细则。

单次运算去重策略：

【单1】舍 q+p，因为有等价的 p+q

【单2】舍 q*p，因为有等价的 p*q

前文说过约束参与运算的左数不大于右数。因而对于加法运算，按这个约束，就可以只取 p+q，而丢弃等价的 q+p。乘法运算的情形类似。

【单3】舍 b-0，因为有等价的 0+b

【单4】舍 0/b，因为有等价的 0*b

【单5】舍 b/1，因为有等价的 1*b

这三个细则可概括为：能用加则不用减，能用乘则不用除。

关联运算去重策略：

对多于一次的运算，即关联运算，定义若干约束细则，以达到所需的去重效果。具体有：

【关1】舍 p-q

减法运算丢弃出现负数的情形，即只取 q-p，而丢弃 p-q。当然这不是因为 p-q 等价于 q-p，而是因为所能涉及到的三种关联运算情形（参见前文部分的说明）都有等价的避免出现负值的等价关联运算，如 r-(p-q) 等价于 r+q-p，而后者不会出现负数。

【关2】舍 a-b-c，因为有等价的 a-(b+c)

【关3】舍 a-(b-c)，因为有等价的 a+c-b

【关4】舍 a+(b-c)，因为有等价的 a+b-c

【关5】舍 a-b+c，因为有等价的 a+c-b

【关6】舍 a/b/c，因为有等价的 a/(b*c)

【关7】舍 a/(b/c)，因为有等价的 a*c/b

【关8】舍 a*(b/c)，因为有等价的 a*b/c

【关9】舍a/b*c，因为有等价的 a*c/b

这六个细则可概括为：多用加少用减，多用乘少用除；先加后减，先乘后除。

【关10】舍 (a+b)+(c+d)，因为有等价的 a+(b+(c+d))

【关11】舍 (a*b)*(c*d)，因为有等价的 a*(b*(c*d))

这两个细则可概括为：去除分组加和分组乘。

CBackwardCalcor::reduct 接口实现

reduct 的实现分为两个部分：去重处理和聚合处理。

 1 void CBackwardCalcor::reduct(EnumOp eOp, size_t seq1, size_t seq2, const std::vector<SExpress>& vecLeft)
 2 {
 3     SExpress& oExp1 = m_vecExpress[seq1];
 4     SExpress& oExp2 = m_vecExpress[seq2];
 5     if (eOp == E_OP_R_SUBST && oExp1.oVal.isZero()) // curb b-0, only use 0+b
 6         return;
 7     if ((eOp == E_OP_DIVIDE || eOp == E_OP_R_DIVIDE) && oExp1.oVal.isZero())
 8         return;
 9     if (eOp == E_OP_DIVIDE && oExp1.oVal.isOne()) // curb b/1, only use 1*b
10         return;
11     if (eOp == E_OP_R_DIVIDE && oExp1.oVal == oExp2.oVal)
12         return;
13     if (isRedundant(oExp1.eOp, oExp2.eOp, eOp))
14     {
15         CLog::LogMsg(LOG_DBG, "base curbed: L=%s, R=%s, Op=%d.", oExp1.strExpress.c_str(), oExp2.strExpress.c_str(), (int)eOp);
16         return;
17     }
18     if (isRedundantEx(oExp1, oExp2, eOp))
19     {
20         CLog::LogMsg(LOG_DBG, "ex curbed: L=%s, R=%s, Op=%d.", oExp1.strExpress.c_str(), oExp2.strExpress.c_str(), (int)eOp);
21         return;
22     }
23 
24     SExpress oReduce;
25     doBiOp(eOp, oExp1, oExp2, oReduce, vecLeft.empty());
26     if (vecLeft.empty())
27     {
28         if (CBackwardCalcor::sm_oAnswer == oReduce.oVal)
29         {
30             if (CLog::instance()->meetLogCond(LOG_DBG))
31             {
32                 CLog::LogMsg(LOG_DBG, "solution: L=%s,R=%s,op=%d => %s", oExp1.strExpress.c_str(), oExp2.strExpress.c_str(), eOp, oReduce.strExpress.c_str());
33                 if (CBackwardCalcor::sm_setResult.find(oReduce.strExpress) != CBackwardCalcor::sm_setResult.end())
34                 {
35                     CLog::LogMsg(LOG_DBG, "solution: met a repeated solution %s", oReduce.strExpress.c_str());
36                 }
37             }
38             CBackwardCalcor::sm_setResult.insert(oReduce.strExpress);
39         }
40         return;
41     }
42     std::vector<SExpress> vecNew = vecLeft;
43     vecNew.push_back(oReduce);
44     CBackwardCalcor oNew(vecNew);
45     oNew.exec();
46 }

exec 接口里是对一级子过程做去重处理，而这里是对二级子过程做去重处理。逐个说明如下：

 5     if (eOp == E_OP_R_SUBST && oExp1.oVal.isZero()) // curb b-0, only use 0+b
 6         return;

0 和数值 b 做反减运算，即 b-0，由细则【单3】，被当作重复的聚合子过程而跳过。

 7     if ((eOp == E_OP_DIVIDE || eOp == E_OP_R_DIVIDE) && oExp1.oVal.isZero())
 8         return;

0 做除数（b/0）以及 0做被除数（0/b）时，对应的聚合子过程都跳过。前者是非法情形，后者与 0*b重复，对应细则【单4】。

 9     if (eOp == E_OP_DIVIDE && oExp1.oVal.isOne()) // curb b/1, only use 1*b
10         return;

b/1 的情形当成重复被跳过，因为与 1*b 等价，对应细则【单5】。

11     if (eOp == E_OP_R_DIVIDE && oExp1.oVal == oExp2.oVal)
12         return;

a、b 两数不等时，需要分别尝试 a/b 和 b/a 两种聚合子过程。a=b 时，只需考虑其中之一，另一个当成重复被跳过。

13     if (isRedundant(oExp1.eOp, oExp2.eOp, eOp))
       ...
18     if (isRedundantEx(oExp1, oExp2, eOp))
       ...

isRedundant 和 isRedundantEx 这两个接口应对前后聚合关联相关的去重处理，放到后面再说。

现在来看 reduct 接口的聚合处理逻辑：

24     SExpress oReduce;
25     doBiOp(eOp, oExp1, oExp2, oReduce, vecLeft.empty());

这两条语句实施左表达式 oExp1 和右表达式 oExp2 的二元聚合运算（由 eOp 指定），聚合后的结果放到局部变量 oReduce 中。doBiOp 接口的实现后面再说。

26     if (vecLeft.empty())
27     {
28         if (CBackwardCalcor::sm_oAnswer == oReduce.oVal)
29         {
30             if (CLog::instance()->meetLogCond(LOG_DBG))
31             {
32                 CLog::LogMsg(LOG_DBG, "solution: L=%s,R=%s,op=%d => %s", oExp1.strExpress.c_str(), oExp2.strExpress.c_str(), eOp, oReduce.strExpress.c_str());
33                 if (CBackwardCalcor::sm_setResult.find(oReduce.strExpress) != CBackwardCalcor::sm_setResult.end())
34                 {
35                     CLog::LogMsg(LOG_DBG, "solution: met a repeated solution %s", oReduce.strExpress.c_str());
36                 }
37             }
38             CBackwardCalcor::sm_setResult.insert(oReduce.strExpress);
39         }
40         return;
41     }

这几行代码的逻辑是如果剩余表达式数组 vecLeft 为空，就说明这时的 oReduce 是根表达式，其取值如果等于指定要计算的目标数值，就找到了一个解，记日志并把这个解加入到解集中。

42     std::vector<SExpress> vecNew = vecLeft;
43     vecNew.push_back(oReduce);
44     CBackwardCalcor oNew(vecNew);
45     oNew.exec();

最后这几行代码是应对 vecLeft 不为空的情形，用 oReduce 和 vecLeft 拼成 vecNew，以 vecNew 为参数实例化一个 CBackwardCalcor 对象（使用第二个构造函数），并调用该对象的 exec 接口对降阶的情形继续求解。

isRedundant 和 isRedundantEx

isRedundant 接口实现前述的【关2】至【关11】等细则，具体如下：

 1 bool CBackwardCalcor::isRedundant(EnumOp eOpL, EnumOp eOpR, EnumOp eOp)
 2 {
 3     /// curb a-b-c, a-(b-c), a+(b-c) and a-b+c
 4     if (eOp == E_OP_R_SUBST || eOp == E_OP_ADD)
 5     {
 6         if (eOpL == E_OP_R_SUBST || eOpR == E_OP_R_SUBST)
 7             return true;
 8     }
 9     /// curb a/b/c, a/(b/c), a*(b/c) and a/b*c
10     if (eOp == E_OP_MULTIPLE || IS_DIVIDE(eOp))
11     {
12         if (IS_DIVIDE(eOpL) || IS_DIVIDE(eOpR))
13             return true;
14     }
15     /// curb (a+b)+(c+d)
16     if (eOp == E_OP_ADD && eOpL == E_OP_ADD && eOpR == E_OP_ADD)
17         return true;
18     /// curb (a*b)*(c*d)
19     if (eOp == E_OP_MULTIPLE && eOpL == E_OP_MULTIPLE && eOpR == E_OP_MULTIPLE)
20         return true;
21 
22     return false;
23 }

isRedundantEx 接口针对连乘和连加的情形做去重处理。实现代码如下：

 1 bool CBackwardCalcor::isRedundantEx(const SExpress& oExp1, const SExpress& oExp2, EnumOp eOp)
 2 {
 3     if (eOp == E_OP_MULTIPLE) // consider a*b*c
 4     {
 5         if (oExp1.eOp != E_OP_MULTIPLE && oExp2.eOp != E_OP_MULTIPLE)
 6             return false;
 7         return (oExp2.eOp != E_OP_MULTIPLE ? true : oExp1.oVal > oExp2.oL);
 8     }
 9     if (eOp == E_OP_ADD) // consider a+b+c
10     {
11         if (oExp1.eOp != E_OP_ADD && oExp2.eOp != E_OP_ADD)
12             return false;
13         return (oExp2.eOp != E_OP_ADD ? true : oExp1.oVal > oExp2.oL);
14     }
15     return false;
16 }

连乘的情形，以 2、3、4 求 24 为例，把2、3、4这三个数连乘便得到24，所以2*3*4 是一个解，按乘法的交换律和结合律，可以衍生出很多类似的解，如：

4*4*(2*3)，2*4*3，3*(2*4)，3*2*4，4*(3*2)，3*4*2，2*(3*4)，4*2*3，4*3*2，...

本程序的处理策略是只留下 2*3*4 这一个解，而其它衍生解当成重复解全被忽略掉。扩展到更一般的情形，就是：如果 k1*k2*...*kn=k，且有 k1 <= k2 <= ... <= kn，则 k1*k2*...*kn 是由 k1、k2、...、kn 求 k 的一个解，而由 k1*k2*...*kn 凭据乘法交换律和结合律衍生出的其它解一律当成重复解被忽略不计。

isRedundantEx 接口里如下三行代码便是应对连乘的去重处理的：

 5         if (oExp1.eOp != E_OP_MULTIPLE && oExp2.eOp != E_OP_MULTIPLE)
 6             return false;
 7         return (oExp2.eOp != E_OP_MULTIPLE ? true : oExp1.oVal > oExp2.oL);

走到这段逻辑的情境是当时正要对左表达式 oExp1 和右表达式 oExp2 做乘法运算，如果 oExp1 与 oExp2 的 eOp 分量都不是 E_OP_MULTIPLE，即不与当前要做的乘法运算构成连乘，这种情形不判为重复；否则就确定碰到了连乘的情形，连乘又分为如下三种情形（oExp1 部分高亮为黄色，oExp2 部分高亮为蓝色）：

1、p*(q*r)

2、(p*q)*r

3、(p*q)*(r*s)

情形3在这里不会碰到，因为在 isRedundant 接口里由【关11】细则就会提前判为重复。

情形2因满足 oExp2.eOp != E_OP_MULTIPLE 而直接判为重复。

情形1判为重复的条件是 oExp1.oVal > oExp2.oL（即 p > q）。

概括来说就是：p、q、r 连乘时，只选取其中最大的两个数先乘的情形，其余的情形全部判为重复。

由 1、 2、3、4 求 24——以这个例子来看一下大值先乘的策略从效果上要好于小值先乘的策略：

大值先乘策略：

1、3*4

2、2*(3*4)　　　　// 去除 2、3、4 三数连乘的其它组合形式

3、1*(2*(3*4)) 　　// 去除 1、2、(3*4) 三数连乘的其它组合形式

对第3步得到的解去括号便是1*2*3*4

小值先乘策略：

1、1*2

2、(1*2)*3　　　　// 去除 1、2、3 三数连乘的其它组合形式

3、4*((1*2)*3) 　　// 去除 4、(1*2)、3 三数连乘的其它组合形式

对第3步得到的解去括号是4*1*2*3

对比不难发现，大值先乘策略总能保证去括号后参与连乘的数由小到大排列；而小值先乘策略则不能保证（例子中第2步1、2、3连乘得积为6，大于最后参与乘法运算的4，按前面的【单2】细则，4要放到乘法的左边）。

连加去重的情形和连乘的情形类似，采用的是大值先加策略。

CBackwardCalcor::doBiOp

doBiOp 接口实现如下：

 1 void CBackwardCalcor::doBiOp(EnumOp eOp, const SExpress& oExp1, const SExpress& oExp2, SExpress& oReduct, bool bNoLeft)
 2 {
 3     oReduct.eOp = eOp;
 4     oReduct.oL = oExp1.oVal;
 5     oReduct.oR = oExp2.oVal;
 6     std::string strHead = (bNoLeft ? "" : "(");
 7     std::string strTail = (bNoLeft ? "" : ")");
 8     switch (eOp)
 9     {
10     case E_OP_ADD:
11     case E_OP_MULTIPLE:
12         oReduct.oVal = (eOp == E_OP_ADD ? fractAdd(oExp1.oVal, oExp2.oVal) : fractMultiply(oExp1.oVal, oExp2.oVal));
13         if (oExp1.oVal == oExp2.oVal && oExp1.strExpress > oExp2.strExpress)
14             oReduct.strExpress = putTogether(oExp2, oExp1, eOp, strHead, strTail);
15         else
16             oReduct.strExpress = putTogether(oExp1, oExp2, eOp, strHead, strTail);
17         break;
18     case E_OP_R_SUBST:
19     case E_OP_DIVIDE:
20         oReduct.oVal = (eOp == E_OP_R_SUBST ? fractAdd(oExp2.oVal, minusByZero(oExp1.oVal)) : 
21             fractMultiply(oExp2.oVal, reciprocal(oExp1.oVal)));
22         if (oExp1.oVal == oExp2.oVal && oExp1.strExpress > oExp2.strExpress)
23             oReduct.strExpress = putTogether(oExp1, oExp2, eOp, strHead, strTail);
24         else
25             oReduct.strExpress = putTogether(oExp2, oExp1, eOp, strHead, strTail);
26         break;
27     case E_OP_R_DIVIDE:
28     default:
29         oReduct.oVal = fractMultiply(oExp1.oVal, reciprocal(oExp2.oVal));
30         oReduct.strExpress = putTogether(oExp1, oExp2, eOp, strHead, strTail);
31         break;
32     }
33 }

该接口实施左表达式 oExp1 和右表达式 oExp2 的二元聚合运算 eOp，聚合结果由输出参数 oReduct 带出，其中 putTogether 是个辅助函数，用来拼接聚合表达式的字符串表示式。当 oExp1 和 oExp2 数值相等时，则比较它们的 strExpress 分量的大小来决定拼接聚合表达式字符串时谁是左数谁是右数。当 eOp 为 E_OP_R_DIVIDE 时，在 doBiOp 里不会出现 oExp1.oVal 等于 oExp2.oVal 的情形，因为在前述的 reduct 接口里这种情形被提前判为重复而不会走到 doBiOp 里。

putTogether 函数实现如下：

 1 std::string putTogether(const SExpress& oExpL, const SExpress& oExpR, EnumOp eOp, 
 2                         const std::string& strHead, const std::string& strTail)
 3 {
 4     std::string strL = oExpL.strExpress, strR = oExpR.strExpress;
 5     if (eOp == E_OP_ADD)
 6     {
 7         if (oExpL.strExpress[0] == '(')
 8             strL = oExpL.strExpress.substr(1, oExpL.strExpress.length() - 2);
 9         if (oExpR.strExpress[0] == '(')
10             strR = oExpR.strExpress.substr(1, oExpR.strExpress.length() - 2);
11     }
12     else if (eOp == E_OP_R_SUBST)
13     {
14         if (oExpL.strExpress[0] == '(')
15             strL = oExpL.strExpress.substr(1, oExpL.strExpress.length() - 2);
16         if (IS_MULTI_OR_DIVE(oExpR.eOp))
17             strR = oExpR.strExpress.substr(1, oExpR.strExpress.length() - 2);
18     }
19     else if (eOp == E_OP_MULTIPLE)
20     {
21         if (IS_MULTI_OR_DIVE(oExpL.eOp))
22             strL = oExpL.strExpress.substr(1, oExpL.strExpress.length() - 2);
23         if (IS_MULTI_OR_DIVE(oExpR.eOp))
24             strR = oExpR.strExpress.substr(1, oExpR.strExpress.length() - 2);
25     }
26     else // divide
27     {
28         if (IS_MULTI_OR_DIVE(oExpL.eOp))
29             strL = oExpL.strExpress.substr(1, oExpL.strExpress.length() - 2);
30     }
31 
32     return strHead + strL + getOpString(eOp) + strR + strTail;
33 }

新拼接出的表达式，如果不是根节点，其 strExpress 分量是带左右括号的：左括号在头部，右括号在尾部。在拼接新的表达式时，参与聚合的子节点为非叶子节点，则根据关联的运算符之间的优先级规则对子节点做去括号处理。比如由 a、b、c、d 求 e，以下是一些可能的聚合例子：

a 和 (b+c) 做加法聚合得到 (a+b+c)

(a+b) 和 (c-d) 做乘法聚合得到 (a+b)*(c-d)

(a*b) 和 c 做除法聚合，分两种情形：(a*b) 做被除数，c 做除数，则得到 (a*b/c)；反过来，c 做被除数的情形，则得到 (c/(a*b))

关于去重处理的补充说明

最早引入去重处理的说法是说去除重复的解。但是上面文字表述过的去重处理策略实际上是广义的去重处理，即尽可能早地做去重处理，而不是等聚合到了根节点再做去重处理，这样的好处是可以减少大量无谓的运算，以便更快地求解，即便是无解的情形也能更快地得出结论。

但是狭义的去重处理逻辑也还是要有的，前面贴了对应的代码实现，只是没有做文字表述。就是 reduct 接口的如下代码段：

30             if (CLog::instance()->meetLogCond(LOG_DBG))
31             {
32                 CLog::LogMsg(LOG_DBG, "solution: L=%s,R=%s,op=%d => %s", oExp1.strExpress.c_str(), oExp2.strExpress.c_str(), (int)eOp, oReduce.strExpress.c_str());
33                 if (CBackwardCalcor::sm_setResult.find(oReduce.strExpress) != CBackwardCalcor::sm_setResult.end())
34                 {
35                     CLog::LogMsg(LOG_DBG, "solution: met a repeated solution %s", oReduce.strExpress.c_str());
36                 }
37             }
38             CBackwardCalcor::sm_setResult.insert(oReduce.strExpress);

更准确地说，就是这个代码段的最后一条语句（其余语句只是记日志相关逻辑），静态成员 sm_setResult 的类型定义成 std::set<std::string> 就是借助 std::set 的特性而实现狭义的去重处理逻辑。

下面以一个实例来说明狭义的去重处理逻辑的必要性，下图是两次用 2、6、4、8 求 24的实际效果演示，头一次记日志，第二次不记日志：

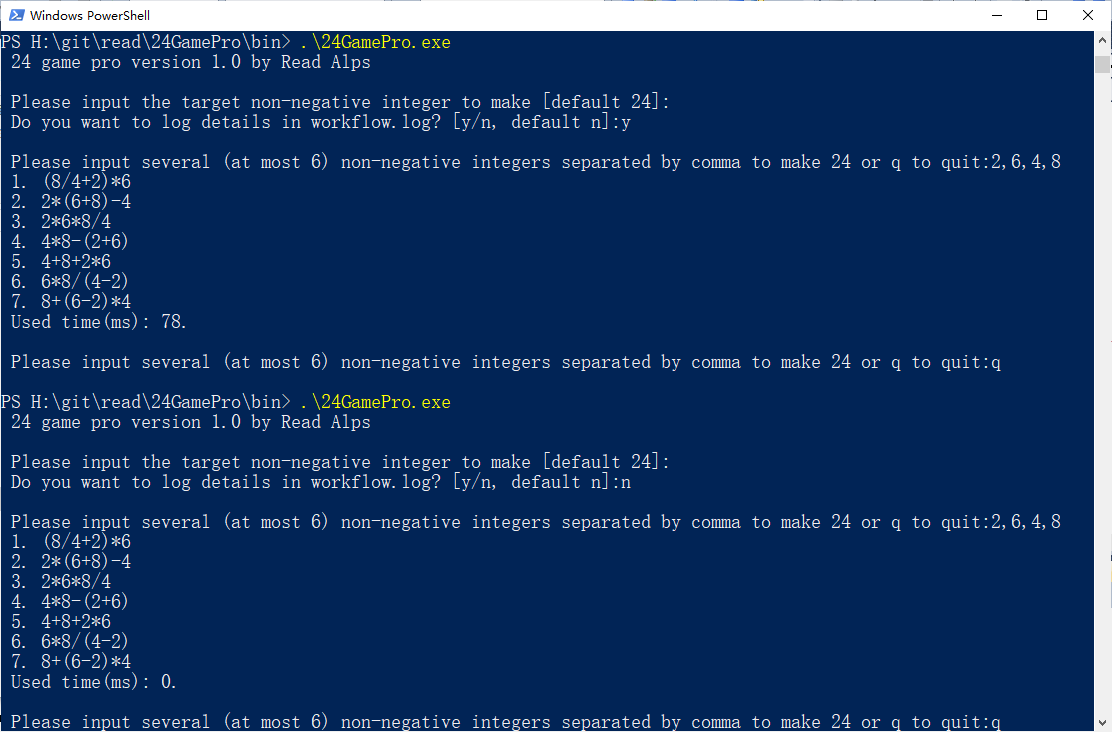
两次得出的求解集是一样的，但用时差别显著，记日志的情况下用了 78 毫秒，不记日志时则为 0 毫秒。

日志文件叫做 workflow.log，日志1529行，97KB，记录了由 2、6、4、8 求 24 的完整求解过程。大致过一下头11行：

 1 2020-09-30 20:55:07.867 [2] Dealing: 2 4 6 8
 2 2020-09-30 20:55:07.867 [2] cur two: L=2, R=4 with 2 pending node(s): 6 8
 3 2020-09-30 20:55:07.867 [2] Dealing: 6 (2+4) 8
 4 2020-09-30 20:55:07.867 [2] cur two: L=6, R=(2+4) with 1 pending node(s): 8
 5 2020-09-30 20:55:07.867 [2] ex curbed: L=6, R=(2+4), Op=1.
 6 2020-09-30 20:55:07.867 [2] Dealing: 8 ((2+4)*6)
 7 2020-09-30 20:55:07.867 [2] cur two: L=8, R=((2+4)*6) with no pending nodes
 8 2020-09-30 20:55:07.867 [2] ex curbed: L=8, R=((2+4)*6), Op=3.
 9 2020-09-30 20:55:07.867 [2] Dealing: (6-(2+4)) 8
10 2020-09-30 20:55:07.868 [2] cur two: L=(6-(2+4)), R=8 with no pending nodes
11 2020-09-30 20:55:07.868 [2] base curbed: L=(6-(2+4)), R=8, Op=1.

第 1 行对应第一个 CBackwardCalcor 实例，对应根任务：由 2、4、6、8 求 24；

第 2 行表示根任务的当前水位为 L=2, R=4，即最低水位，要对最小的两个数 2 和 4 做聚合运算，6 和 8 进剩余表达式数组；

第 3 行，Dealing: 6 (2+4) 8，表示根任务对 2 和 4 做了加法聚合运算，得到 (2+4)，然后实例化了第二个 CBackwardCalcor 对象，执行子任务1：由 (2+4) 与剩余的 6 和 8 求 24；

第 4 行，子任务1的当前水位为 L=6, R=(2+4)，8 进剩余表达式数组；

第 5 行，ex curbed: L=6, R=(2+4), Op=1，表示子任务1要对 6 和 (2+4) 做加法运算，这是连加的情形，由于不符合前述的大数先加策略，视为重复被跳过；

第 6 行，Dealing: 8 ((2+4)*6)，表示子任务1对 (2+4) 和 6 做了乘法运算，得到 ((2+4)*6)，然后实例化了第三个 CBackwardCalcor 对象，执行子任务1-1：由 ((2+4)*6) 与剩余的 8 求 24；

第 7 行，子任务1-1的当前水位（也是唯一水位）为 L=8, R=((2+4)*6)，剩余表达式数组为空；

第 8 行，ex curbed: L=8, R=((2+4)*6), Op=3，表示子任务1-1要对 8 和 ((2+4)*6) 做乘法运算，这是连乘的情形，由于不符合前述的大数先乘策略，视为重复被跳过；

子任务1-1会对 8 和 ((2+4)*6) 实施其它二元运算，但由于 8+36、36-8、8/36、36/8 都不等于 24，所以子任务1-1里没有解。

第９行，Dealing: (6-(2+4)) 8，表示子任务1对 (2+4) 和 6 做了减法运算，得到 (6-(2+4))，然后实例化了第四个 CBackwardCalcor 对象，执行子任务1-2：由 (6-(2+4)) 与剩余的 8 求 24；

第 10 行，子任务1-2的当前水位（也是唯一水位）为 L=(6-(2+4)), R=8，剩余表达式数组为空；

第 11 行，base curbed: L=(6-(2+4)), R=8, Op=1，表示子任务1-2对 (6-(2+4)) 和 8 做加法运算，不符合先加后减策略，视为重复被跳过。

现在来看日志文件里记录到的狭义去重的信息，在日志文件里查找关键字 repeated，存在如下两处：

1054 2020-09-30 20:55:07.899 [2] solution: met a repeated solution 4*8-(2+6)
...
1339 2020-09-30 20:55:07.899 [2] solution: met a repeated solution 6*8/(4-2)

具体看一下第一个重复解是如何发生的。在日志文件里查找关键字 4*8-(2+6)，找到第一次求得这个解的相关日志，如下：

 233 2020-09-30 20:55:07.875 [2] cur two: L=2, R=6 with 2 pending node(s): 4 8
 234 2020-09-30 20:55:07.875 [2] Dealing: 4 8 (2+6)
 235 2020-09-30 20:55:07.875 [2] cur two: L=4, R=8 with 1 pending node(s): (2+6)
 236 2020-09-30 20:55:07.875 [2] Dealing: (2+6) (4+8)
 237 2020-09-30 20:55:07.875 [2] cur two: L=(2+6), R=(4+8) with no pending nodes
 238 2020-09-30 20:55:07.875 [2] base curbed: L=(2+6), R=(4+8), Op=1.
 239 2020-09-30 20:55:07.875 [2] Dealing: (2+6) (4*8)
 240 2020-09-30 20:55:07.875 [2] cur two: L=(2+6), R=(4*8) with no pending nodes
 241 2020-09-30 20:55:07.875 [2] ex curbed: L=(2+6), R=(4*8), Op=1.
 242 2020-09-30 20:55:07.875 [2] ex curbed: L=(2+6), R=(4*8), Op=3.
 243 2020-09-30 20:55:07.875 [2] solution: L=(2+6),R=(4*8),op=2 => 4*8-(2+6)

由匹配的第243行日志，往前找到根任务当时对应的水位是 L=2, R=6，在这个水位，先对 2 和 6 做加法运算，得到 (2+6)；然后对剩余的 4 和 8 做乘法运算，得到 (4*8)；最后再对 (2+6) 和 (4*8) 做反减运算，得到 4*8-(2+6) 这个解。

继续在日志文件里往后查找 4*8-(2+6)：

1053 2020-09-30 20:55:07.899 [2] solution: L=(2+6),R=(4*8),op=2 => 4*8-(2+6)
1054 2020-09-30 20:55:07.899 [2] solution: met a repeated solution 4*8-(2+6)

在日志文件里往前查找 with 2 pending：

986 2020-09-30 20:55:07.897 [2] cur two: L=4, R=8 with 2 pending node(s): 2 6

这说明第二次求得 4*8-(2+6) 这个解时，当时根任务所在的水位是 L=4, R=8，在这个水位，先对 4 和 8 做乘法运算，得到 (4*8)；然后对剩余的 2 和 6 做加法运算，得到 (2+6)；最后再对 (2+6) 和 (4*8) 做反减运算，再一次得到 4*8-(2+6) 这个解。

日志记录相关代码实现

头文件log.h

 1 #ifndef LOG_MGR_H
 2 #define LOG_MGR_H
 3 
 4 #include "common.h"
 5 #include <stdio.h>
 6 
 7 enum EnumLogLevel
 8 {
 9     LOG_ERR = 0,
10     LOG_WRN = 1,
11     LOG_DBG = 2
12 };
13 
14 class CLog
15 {
16 public:
17     void setLogPathAndName(const char* pPath, const char* pszName);
18     static void LogMsg(u8 ucLevel, char* pszFmt, ...);
19     static void LogMsgS(u8 ucLevel, const char* pszMsg);
20     u8 getLogLevel()
21     {
22         return m_ucLevel;
23     }
24     void setLogLevel(u8 ucLevel)
25     {
26         if (ucLevel >= LOG_ERR && ucLevel <= LOG_DBG)
27             m_ucLevel = ucLevel;
28     }
29     bool meetLogCond(u8 ucLevel)
30     {
31         return (NULL != m_pFile && ucLevel <= m_ucLevel);
32     }
33 
34     static CLog* instance()
35     {
36         if (NULL == sm_poInstance)
37             sm_poInstance = new CLog();
38         return sm_poInstance;
39     }
40 
41 private:
42     CLog()
43     {
44         m_pFile = NULL;
45         m_ucLevel = LOG_ERR;
46     }
47     void LogMsgInner(u8 ucLevel, const char* pszMsg);
48 
49 private:
50     std::string m_strAbsFile;
51     u8 m_ucLevel;
52     FILE* m_pFile;
53 
54     static CLog* sm_poInstance;
55 };
56 
57 #endif

实现文件log.cpp

 1 #include "common.h"
 2 #include "log.h"
 3 #include <stdarg.h>
 4 #include <ctime>
 5 #include <sys/timeb.h>
 6 using namespace std;
 7 
 8 CLog* CLog::sm_poInstance = NULL;
 9 
10 void CLog::setLogPathAndName(const char* pPath, const char* pszName)
11 {
12     m_strAbsFile = std::string(pPath) + pszName;
13     m_pFile = fopen(m_strAbsFile.c_str(), "a+");
14 }
15 
16 void CLog::LogMsg(u8 ucLevel, char* pszFmt, ...)
17 {
18     if (!CLog::instance()->meetLogCond(ucLevel))
19         return;
20 
21     std::string strMsg;
22     size_t uiLen = 0;
23     {
24         va_list va;
25         va_start(va, pszFmt);
26 #ifdef _WINDOWS
27         uiLen = _vsnprintf(NULL, 0, pszFmt, va);
28 #else
29         uiLen = vsnprintf(NULL, 0, pszFmt, va);
30 #endif
31         va_end(va);
32     }
33 
34     if (uiLen > 0)
35     {
36         strMsg.resize(uiLen);
37 
38         va_list va;
39         va_start(va, pszFmt);
40 #ifdef _WINDOWS
41         _vsnprintf(((char*)strMsg.c_str()), uiLen + 1, pszFmt, va);
42 #else
43         vsnprintf(((char*)strMsg.c_str()), uiLen + 1, pszFmt, va);
44 #endif
45         va_end(va);
46     }
47     sm_poInstance->LogMsgInner(ucLevel, strMsg.c_str());
48 }
49 
50 void CLog::LogMsgS(u8 ucLevel, const char* pszMsg)
51 {
52     if (CLog::instance()->meetLogCond(ucLevel))
53         sm_poInstance->LogMsgInner(ucLevel, pszMsg);
54 }
55 
56 void getCurrentTimeString(char* pszOut)
57 {
58     tm* pTm;
59     timeb oTimeb;
60     ftime(&oTimeb);
61     pTm = localtime(&oTimeb.time);
62     sprintf(pszOut, "%04d-%02d-%02d %02d:%02d:%02d.%03d",  
63         pTm->tm_year + 1900, pTm->tm_mon + 1, pTm->tm_mday, pTm->tm_hour, pTm->tm_min, pTm->tm_sec, oTimeb.millitm);  
64 }
65 
66 void CLog::LogMsgInner(u8 ucLevel, const char* pszMsg)
67 {
68     char szDateTime[64];
69     getCurrentTimeString(szDateTime);
70     char szLogLevel[6] = " [2] ";
71     if (ucLevel != 2)
72         szLogLevel[2] = '0' + ucLevel;
73     strcat(szDateTime, szLogLevel);
74     fprintf(m_pFile, szDateTime);
75     fprintf(m_pFile, pszMsg);
76     fprintf(m_pFile, "\n");
77     fflush(m_pFile);
78 }

公共基础函数实现

common.h

 1 #ifndef CMN_H
 2 #define CMN_H
 3 
 4 #include <stdint.h>
 5 #include <string>
 6 #include <vector>
 7 #ifdef _LINUX
 8 #include <string.h>
 9 #endif
10 using namespace std;
11 
12 #ifdef _WINDOWS
13 #define DIR_SLASH       '\\'
14 #define DIR_SLASH_STR   "\\"
15 #else
16 #define DIR_SLASH       '/'
17 #define DIR_SLASH_STR   "/"
18 #endif
19 
20 typedef uint64_t u64;
21 typedef uint32_t u32;
22 typedef uint8_t u8;
23 
24 void trimString(std::string& strTrim);
25 bool separateString(const std::string& strSrc, const char* pszSep, std::string& strHead, std::string& strTail, bool bFromLeft);
26 void divideString2Vec(const std::string& strInput, const char* pszSep, std::vector<std::string>& vecOut);
27 bool shiftToU32(std::string& strVal, u32& uiVal);
28 bool isIntStrVec(std::vector<std::string>& vecVal);
29 std::string u32ToStr(u32 uiVal);
30 #ifdef _LINUX
31 u32 GetTickCount();
32 #endif
33 
34 std::string getMainPath();
35 
36 #endif

common.cpp

  1 #include "common.h"
  2 #ifdef _WINDOWS
  3 #include <direct.h>
  4 #include <windows.h>
  5 #else
  6 #include <stdio.h>
  7 #include <stdlib.h>
  8 #include <unistd.h>
  9 #include <time.h>
 10 #include <sys/time.h>
 11 u32 GetTickCount()
 12 {
 13     timespec ts;
 14     clock_gettime(CLOCK_MONOTONIC, &ts);
 15     return (u32)(ts.tv_sec * 1000 + ts.tv_nsec / 1000000);
 16 }
 17 #endif
 18 
 19 void trimString(std::string& strTrim)
 20 {
 21     size_t iHeadPos = strTrim.find_first_not_of(" \t");
 22     if (iHeadPos == std::string::npos)
 23     {
 24         strTrim = "";
 25         return;
 26     }
 27     size_t iTailPos = strTrim.find_last_not_of(" \t");
 28     if (strTrim.length() != iTailPos + 1)
 29         strTrim.erase(iTailPos + 1);
 30     if (0 != iHeadPos)
 31         strTrim.erase(0, iHeadPos);
 32 }
 33 
 34 bool separateString(const std::string& strSrc, const char* pszSep, std::string& strHead, std::string& strTail, bool bFromLeft)
 35 {
 36     std::string::size_type iPos = (bFromLeft ? strSrc.find(pszSep) : strSrc.rfind(pszSep));
 37     if (iPos == std::string::npos)
 38     {
 39         strHead = strSrc;
 40         trimString(strHead);
 41         strTail = "";
 42         return false;
 43     }
 44 
 45     if (0 == iPos)
 46         strHead = "";
 47     else
 48     {
 49         strHead = strSrc.substr(0, iPos);
 50         trimString(strHead);
 51     }
 52     if (strSrc.length() == iPos + strlen(pszSep))
 53         strTail = "";
 54     else
 55     {
 56         strTail = strSrc.substr(iPos + strlen(pszSep));
 57         trimString(strTail);
 58     }
 59     return true;
 60 }
 61 
 62 void divideString2Vec(const std::string& strInput, const char* pszSep, std::vector<std::string>& vecOut)
 63 {
 64     std::string strHead, strTail;
 65     std::string strRights = strInput;
 66     while (!strRights.empty())
 67     {
 68         separateString(strRights, pszSep, strHead, strTail, true);
 69         trimString(strHead);
 70         if (!strHead.empty())
 71             vecOut.push_back(strHead);
 72         trimString(strTail);
 73         strRights = strTail;
 74     }
 75 }
 76 
 77 bool isIntStr(const std::string& strVal)
 78 {
 79     if (strVal.empty())
 80         return false;
 81     size_t len = strVal.length();
 82     if (len >= 10)
 83         return false;
 84     for (size_t idx = 0; idx < len; ++idx)
 85     {
 86         if (strVal[idx] < '0' || strVal[idx] > '9')
 87             return false;
 88     }
 89     return true;
 90 }
 91 
 92 bool shiftToU32(std::string& strVal, u32& uiVal)
 93 {
 94     trimString(strVal);
 95     if (strVal.empty())
 96     {
 97         uiVal = 24;
 98         return true;
 99     }
100     if (!isIntStr(strVal))
101         return false;
102     uiVal = strtoul(strVal.c_str(), 0, 10);
103     return true;
104 }
105 
106 std::string u32ToStr(u32 uiVal)
107 {
108     char szBuf[128];
109     sprintf(szBuf, "%u", uiVal);
110     return szBuf;
111 }
112 
113 bool isIntStrVec(std::vector<std::string>& vecVal)
114 {
115     if (vecVal.empty())
116         return false;
117     for (size_t idx = 0; idx < vecVal.size(); ++idx)
118     {
119         if (!isIntStr(vecVal[idx]))
120             return false;
121     }
122     return true;
123 }
124 
125 static std::string s_strMainPath;
126 std::string getMainPath()
127 {
128     if (!s_strMainPath.empty())
129         return s_strMainPath;
130 
131     char szBuff[512];
132 #ifdef _WINDOWS
133     GetModuleFileName(NULL, szBuff, 512);
134     std::string strAbsFile = szBuff;
135     size_t iPos = strAbsFile.rfind(DIR_SLASH);
136     s_strMainPath = strAbsFile.substr(0, iPos + 1);
137 #else
138     getcwd(szBuff, 512);
139     s_strMainPath = std::string(szBuff) + "/";
140 #endif
141     return s_strMainPath;
142 }

关于处理性能

本程序处理由5个以及少于5个非负整数反求 24（或其它非负整数）是非常快的，如：

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:8,3,3,3
1. (3+3-3)*8
2. 3*(3+8-3)
3. 3*3*8/3
4. 3+3*8-3
Used time(ms): 0.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:8,45,34,23,67
1. 34-((23+67)/45+8)
2. 45+67-8*(34-23)
Used time(ms): 63.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:65,67,33,245,27
1. 33-(65+245-67)/27
Used time(ms): 78.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:89,67,34,5
From 89,67,34,5, there is no solution to make 24 by using +-*/ and ().
Used time(ms): 0.

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:89,67,34,5,6
1. (34+5*(89-67))/6
2. 6*(67+89)/(5+34)
Used time(ms): 47.

但是参与运算的非负整数总数增加到6或更高时，由于完全求解所涉及的运算量呈指数级增长，所需的时间也呈指数级增长，6个数的求解时长已经达到了秒级，如：

Please input several (at most 6) non-negative integers separated by comma to make 24 or q to quit:89,67,34,5,6,87
1. (34+67-5)/(6+87-89)
2. (5+67-(89-87)*34)*6
3. 34+67+5*89-6*87
4. 34+89-((5+67)/6+87)
5. 34-((5+6)*87-67)/89
6. 34-(67+87-(5+89))/6
7. 5*34-(89-87)*(6+67)
8. 5+(6+34*87)/(67+89)
9. 6*(34-5)/87+89-67
10. 6*89-(87-(5+67))*34
11. 6+5*34/(89-87)-67
12. 67+89-(5+6+34+87)
Used time(ms): 3110.

也因为这个原因，本程序设置了最多6个数的限制。

目前是单线程实现的，可以考虑用多线程并发处理，即对根任务按水位分解成多个子任务交给多个处理线程并发处理。但如果参与运算的数太多的话，多线程机制也作用不大，应该还是要从算法上想更好的办法。

完整代码文件

完整代码文件可以从如下位置提取：

https://github.com/readalps/24GamePro

其中 prj 目录下为 Windows 平台使用的工程文件；makefile 用于 Linux 平台；src 目录下为代码文件，7个文件总体代码约850行。

posted on 2020-10-01 23:47 readalps 阅读(1329) 评论(0) 编辑收藏举报

刷新页面返回顶部