线性代数-二次型-坐标变换笔记

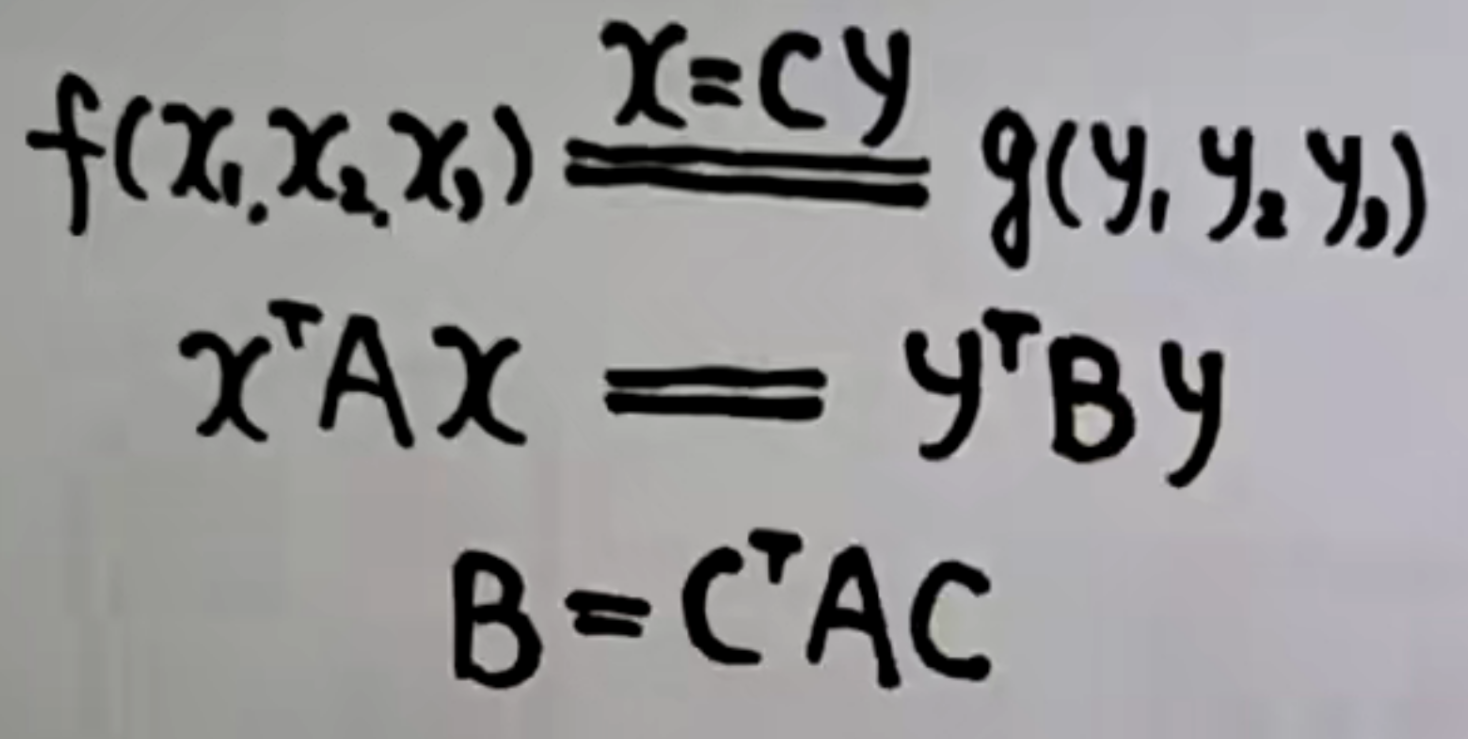
原来的二次型\(f\left ( x_{1},x_{2},x_{3} \right )\)经过坐标变换变成了\(g\left ( y_{1},y_{2},y_{3} \right )\)这个新的二次型

$x^{\mathrm{T}}Ax $ 经过坐标变换变成 $y^{\mathrm{T}}By $ 原来的二次型矩阵\(A\)变成了\(B\) (也是实对称矩阵)

\(A\)和\(B\)之间的之间的关系是\(B = C^{\mathrm{T}}AC\) 其中\(C\)为坐标变换里的可逆矩阵(\(|C| ≠ 0\))

注: 经过坐标变换的二次型的正(负)惯性指数不变