多重背包III

多重背包III(单调队列优化)

原题链接：https://www.acwing.com/problem/content/6/

回忆一下完全背包优化

多重背包III思路

彩色铅笔大佬的题解

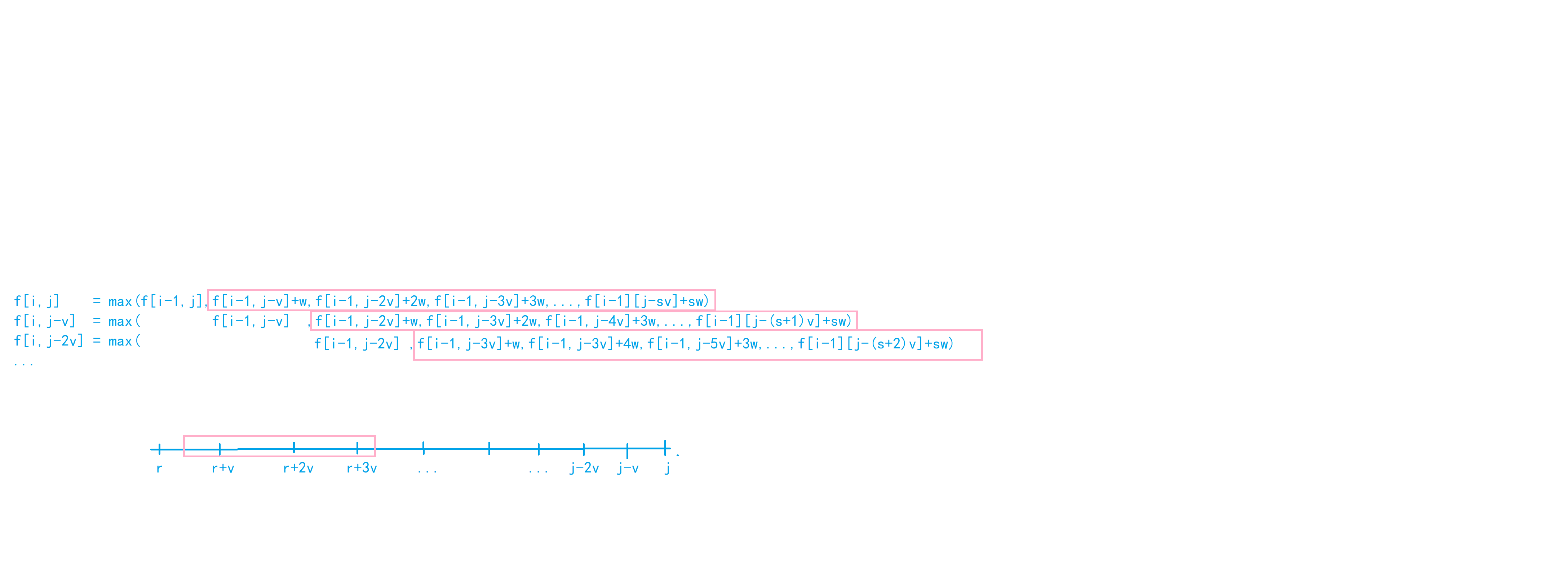
补充：

while(head <= tail && f[i-1][q[tail]]+(j-q[tail])/v[i]*w[i] <= f[i-1][j]) tail --;是为了保证单调队列严格单调下降(队头为最大值)，
f[i-1][q[tail]]是刚才的队尾(当前其实已经是j，但j还未加进去，现在正在保证队列单调性),
(j-q[tail])/v[i]是统计队尾和j之间差了k个数，乘w[i]是因为实际上队尾和j之间还差了k个w[i]

代码

二维

#include<iostream>

using namespace std;

const int N = 1010,M = 20010;

int n,m;
int v[N],w[N],s[N];
int f[N][M];
int q[M]; // 数组模拟队列

int main()
{
    cin >> n >> m ; 
    for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1;i <= n;i ++)
    {
        for(int r = 0; r < v[i]; r ++)
        {
            int head = 0,tail = -1;
            for(int j = r; j <= m;j += v[i])
            {
                // 判断队头是否滑出
                if(head <= tail && q[head] < j-s[i]*v[i]) head ++;
                // 保证模拟队列递减(队头为最大值)
                while(head <= tail && f[i-1][q[tail]]+(j-q[tail])/v[i]*w[i] <= f[i-1][j]) tail --;
                q[++ tail] = j;
                f[i][j] = max(f[i][j],f[i-1][q[head]] + (j-q[head])/v[i]*w[i]);
            }
        }
    }
    cout << f[n][m];
    return 0;
}

一维

#include<iostream>
#include<cstring>

using namespace std;

const int N = 1010,M = 20010;

int n,m;
int v[N],w[N],s[N];
int f[M],g[M];
int q[M]; // 数组模拟队列

int main()
{
    cin >> n >> m ; 
    for(int i = 1;i <= n;i ++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1;i <= n;i ++)
    {
        memcpy(g,f,sizeof g);
        for(int r = 0; r < v[i]; r ++)
        {
            int head = 0,tail = -1;
            for(int j = r; j <= m;j += v[i])
            {
                // 判断队头是否滑出
                if(head <= tail && q[head] < j-s[i]*v[i]) head ++;
                // 保证模拟队列递减(队头为最大值)
                while(head <= tail && g[q[tail]]+(j-q[tail])/v[i]*w[i] <= g[j]) tail --;
                q[++ tail] = j;
                f[j] = max(f[j],g[q[head]] + (j-q[head])/v[i]*w[i]);
            }
        }
    }
    cout << f[m];
    return 0;
}