最长上升子序列模型
最长上升子序列模型
裸模板题：https://www.acwing.com/problem/content/897/
优化版：https://www.acwing.com/problem/content/898/
AcWing 1017. 怪盗基德的滑翔翼
原题链接:https://www.acwing.com/problem/content/1019/
思路：
先审题，确定一个起点，一个方向。求下降最长距离方案。
其实就是求每个点向左向右两个方向的最长下降子序列咯
那么正着来一遍线性dp求最长上升子序列，反着来一遍求最长上升子序列，找出最大值即可。
线性DP：
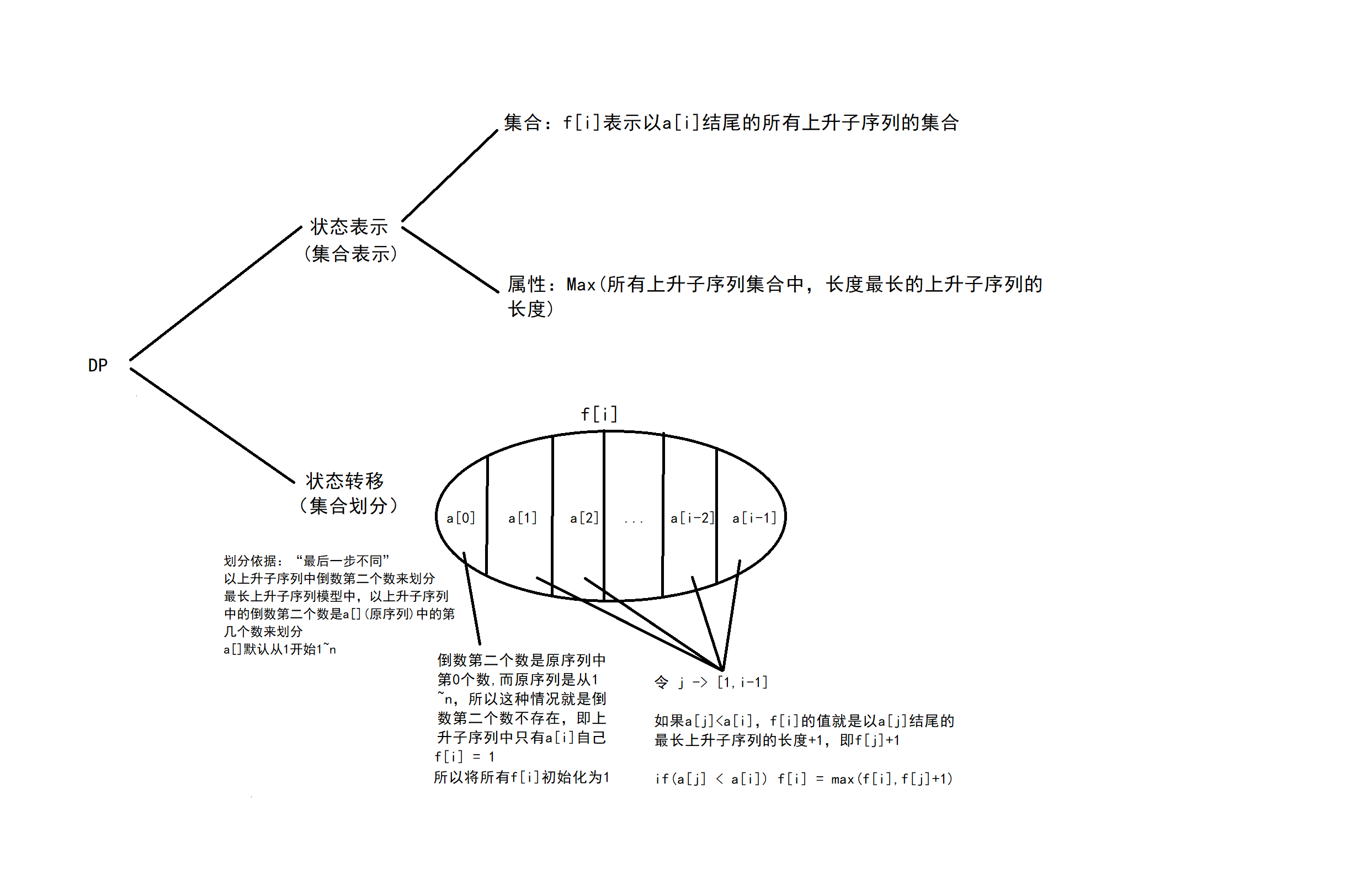
代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int n,k,a[N],f[N];
int main()
{
cin >> k;
while(k --)
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> a[i];
int res = 0;
for(int i = 1; i <= n; i ++) f[i] = 1;
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j < i; j ++)
{
if(a[j] < a[i]) f[i] = max(f[i],f[j] + 1);
}
res = max(res,f[i]);
}
for(int i = 1; i <= n; i ++) f[i] = 1;
for(int i = n; i >= 1; i --)
{
for(int j = n; j > i ; j --)
{
if(a[j] < a[i]) f[i] = max(f[i],f[j] + 1);
}
res = max(res,f[i]);
}
cout << res << endl;
}
return 0;
}
AcWing 1014. 登山
原题链接:https://www.acwing.com/problem/content/1016/
解剖题目
每次所浏览景点的编号都要大于前一个浏览景点的编号，说明是一个严格的子序列。
另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。，说明大家登山，先是一个上升序列，然后到达某个点，接着一个下降序列。
思路
和怪盗基德这个题一样，求一遍最长上升子序列，再反着求一遍最长上升子序列
即每一个点，都求得了以该点结尾的最长上升子序列和以该点开始的最长下降子序列
然后枚举每一个点，求最大值更新答案res = max(f[i]+g[i]-1,res)
DP分析同怪盗基德的滑翔翼
代码
#include<iostream>
using namespace std;
const int N = 1010;
int n,a[N],f[N],g[N];
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i ++) scanf("%d",&a[i]);
for(int i = 1; i <= n; i ++) f[i] = 1,g[i] = 1;
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j < i; j ++)
if(a[j] < a[i]) f[i] = max(f[i],f[j] + 1);
}
for(int i = n ; i >= 1; i --)
{
for(int j = n; j > i; j --)
if(a[j] < a[i]) g[i] = max(g[i],g[j] + 1);
}
int res = 0;
for(int i = 1; i <= n; i ++) res = max(res,f[i]+g[i]-1);
printf("%d",res);
return 0;
}
AcWing 482. 合唱队形
原题链接：https://www.acwing.com/problem/content/484/
解剖题目
出列$ n-k $个同学，剩下 $ k $ 个同学的身高满足上升后有下降。
求最少出列的同学是多少，就是让k最大，就是让这个最长上升下降子序列最长。
即同登山问题
代码
#include<iostream>
using namespace std;
const int N = 110 ;
int n,a[N];
int f[N],g[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> a[i];
for(int i = 1; i <= n; i ++) f[i] = 1,g[i] = 1;
for(int i = 1; i <= n ;i ++)
{
for(int j = 1; j < i ; j ++)
if(a[j] < a[i]) f[i] = max(f[i],f[j] + 1);
}
for(int i = n; i >= 1; i --)
{
for(int j = n; j > i; j --)
if(a[j] < a[i]) g[i] = max(g[i],g[j] + 1);
}
int k = 0;
for(int i = 1; i <= n; i ++) k = max(k,f[i]+g[i]-1);
cout << n-k << endl;
return 0;
}
AcWing 1012. 友好城市
原题链接：https://www.acwing.com/problem/content/1014/
解剖题目(转换成模型)
南北两岸岸上都有位置不同的N个城市，北岸的每个城市都有且只有一个友好城市在南安，不同城市的友好城市不同。
可以看成给了一个边集合，集合中每条边的两个端点都没有重合。
现在要求从中选出尽可能多的边，并且不会出现相交的情况。
做法：
先按照边集的左顶点排序，然后看两个集合：
左端点集合找：符合不相交条件的城市集合，
右端点集合找：上升子序列集合。
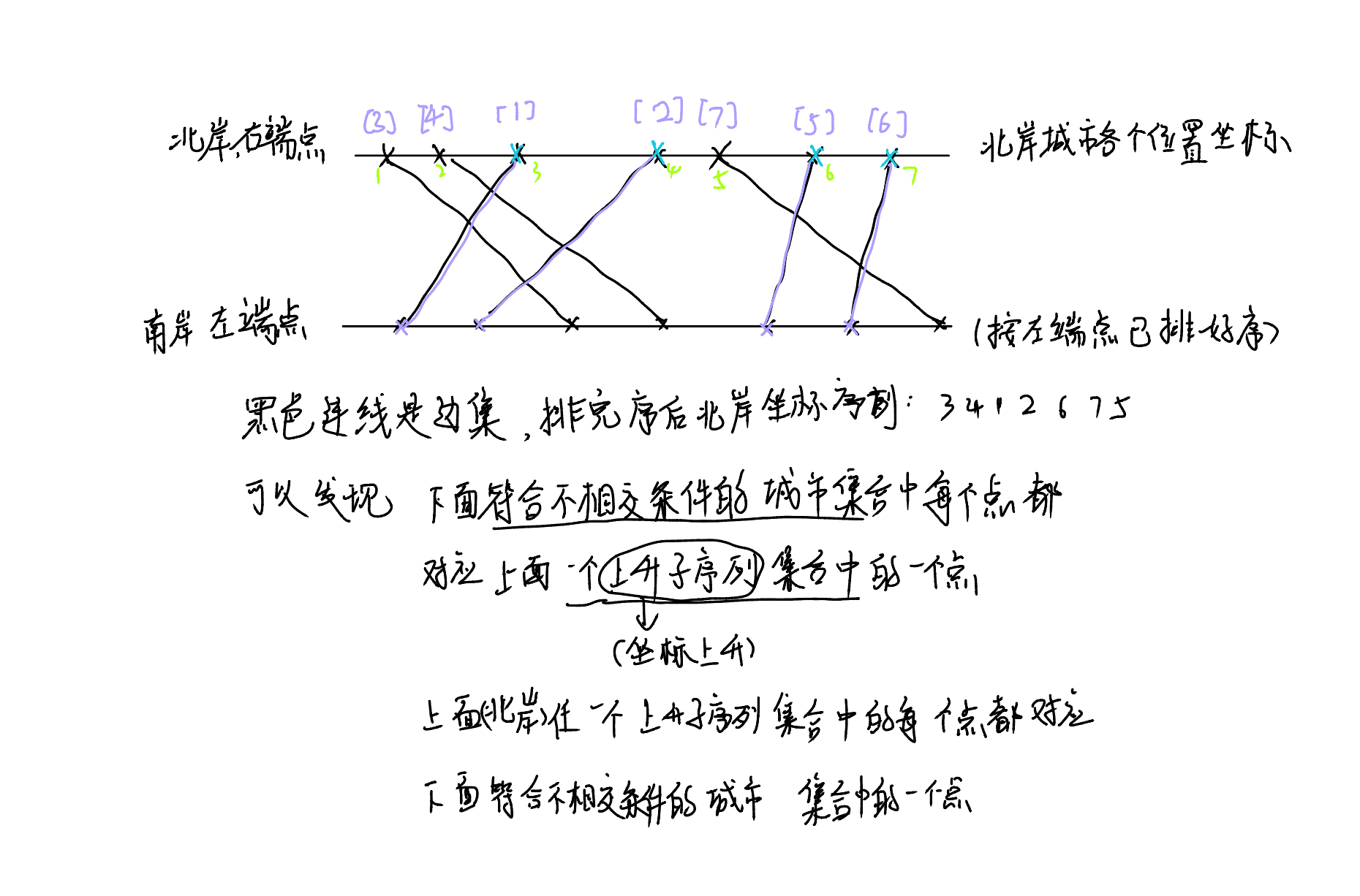
因此两个集合的元素是一一对应，具有映射关系的。
我们就直接去求排完序之后北岸的最长上升子序列即可。
代码
#include<iostream>
#include<algorithm>
using namespace std;
typedef pair<int ,int> PII;
const int N = 5010;
int n;
PII city[N];
int f[N];
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i ++) scanf("%d%d",&city[i].first,&city[i].second);
sort(city,city+n);
int res = 0;
for(int i = 1; i <= n;i ++)
{
f[i] = 1;
for(int j = 1; j < i; j ++)
if(city[j].second < city[i].second) f[i] = max(f[i],f[j] + 1);
res = max(res,f[i]);
}
printf("%d",res);
return 0;
}
AcWing 1016. 最大上升子序列和
原题链接：https://www.acwing.com/problem/content/1018/
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n,a[N];
int f[N];
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i ++) scanf("%d",&a[i]);
int ans = 0;
for(int i = 1; i <= n; i ++)
{
f[i] = a[i];
for(int j = 1; j < i; j ++)
if(a[j] < a[i]) f[i] = max(f[i],f[j] + a[i]);
ans = max(ans,f[i]);
}
printf("%d",ans);
return 0;
}
AcWing 1010. 拦截导弹
原题链接：https://www.acwing.com/problem/content/1012/
题目解剖
第一问是一个最长上升子序列问题
主要看第二问，让求这样最长上升子序列的个数。
贪心写：
贪心做法流程：
从前往后扫描每个数，对于每个数有两种情况：
1.如果现有的子序列的结尾都小于当前数，则创建新的子序列
2.将当前数放到结尾大于等于它的最小的子序列的后面
做法的证明:
设A为贪心得到的答案，B为最优解
证明 A = B就要证明 B<=A , A<=B
证明：
1.B<=A
B是答案的一种，所以B<=A
2.A<=B(调整法)
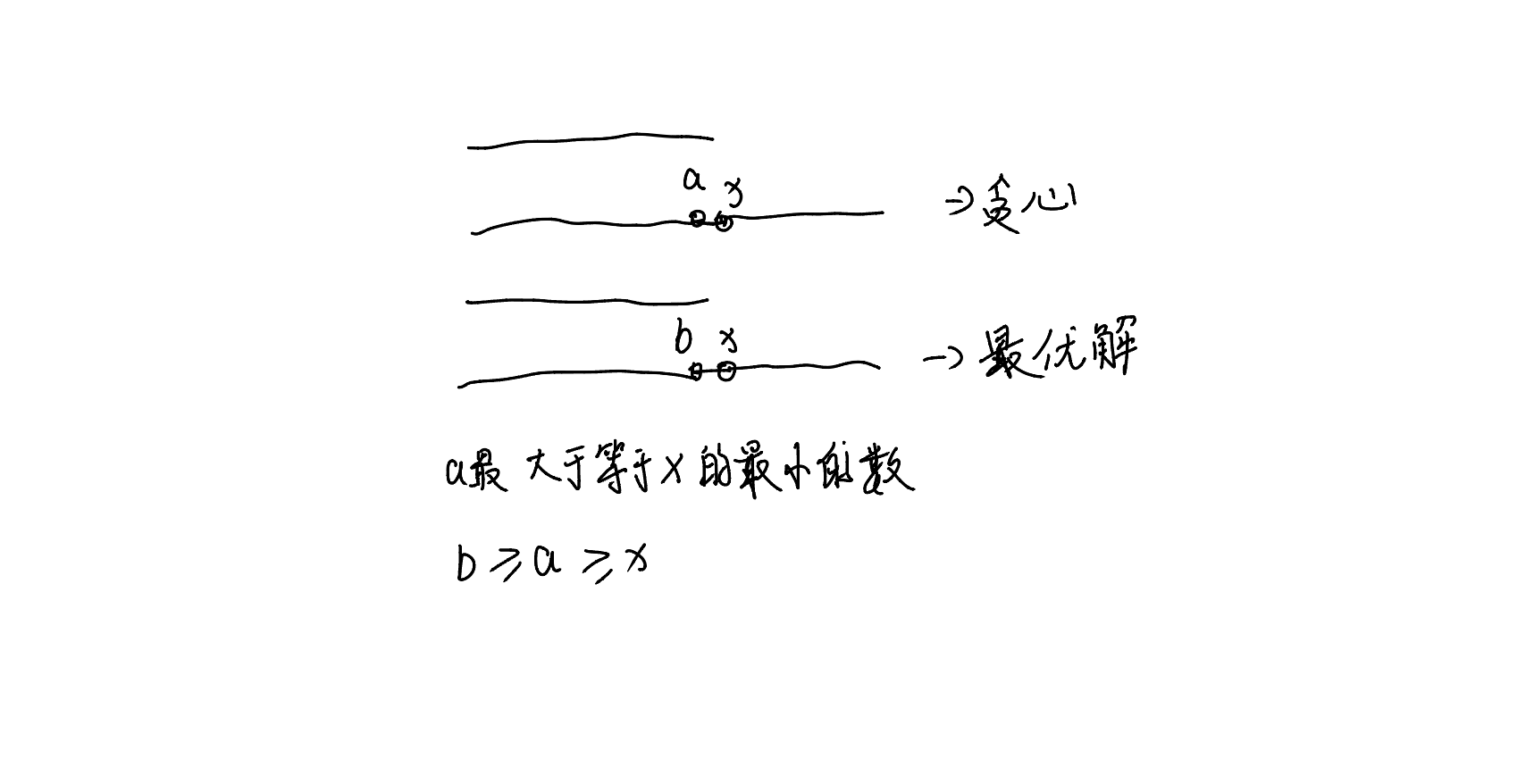
假设找到的最优解方案和贪心的方案不同，如上图，贪心方案是把x加到以a结尾的子序列的后面，最优解是把x加到以b结尾的子序列的后面
a >= b，所以x以及之后的数加到a后面或者b后面都是合法的且子序列个数不变。
因此贪心方案可以和最优解方案相互转换，贪心方案可以转换成最优解，即最优解包括贪心方案，所以A<=B
贪心做法实现：
开一个g[]数组，保存所有已经开好的子序列结尾的数
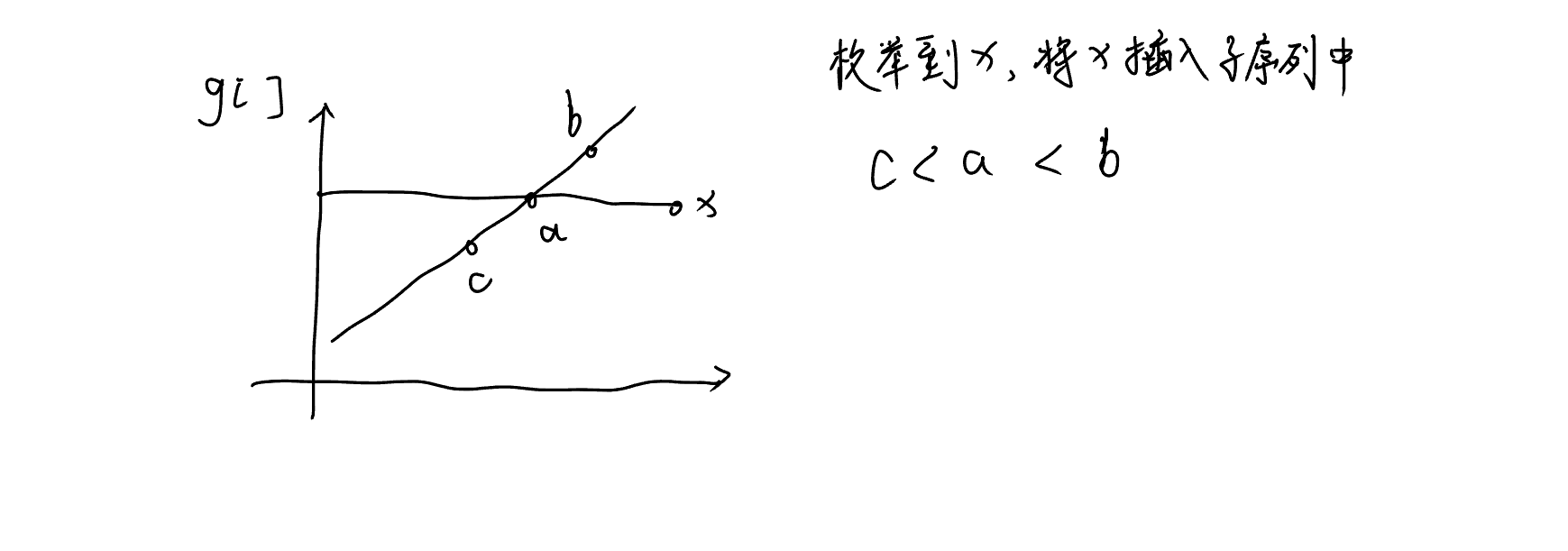
现在枚举到x，要将根据贪心做法插入到某个子序列的结尾，假设找到的大于等于x的最小的数是a，所以x <= a，且c < x
那么让x作为以a结尾的子序列的结尾，体现在图中(g[]中)就是把a替换掉。
c < a < b，所以 c < x <= a <= b ，将a替换掉 c < x <= b。并且可以看到g[]一定是单调递增的.
单调递增(或者说单调不减，这具有二分性) => 直接从小到大枚举判断就行($ O(n^2) $),因为是单调递增的，也所以也可以使用二分来做( $ O(nlogn) $ )。
代码
\(O(n^2)\)做法：
#include<iostream>
#include<algorithm>
#include<sstream> // 数据量过大的时候用
using namespace std;
const int N = 1010;
int n,f[N],a[N],g[N];
int main()
{
string line;
getline(cin,line);
stringstream ssin(line);
while(ssin >> a[n]) n ++;
// 求最长不升子序列
int res = 0;
for(int i = n-1; i >= 0; i --)
{
f[i] = 1;
for(int j = n-1; j > i;j --)
if(a[j] <= a[i]) f[i] = max(f[i],f[j] + 1);
res = max(f[i],res);
}
cout << res << endl;
// 求最长不升子序列个数
int cnt = 0; // 保存子序列的个数
for(int i = 0; i < n; i ++)
{
// 枚举到的子序列
int k = 0;
while(k < cnt && g[k] < a[i]) k ++;
g[k] = a[i]; // 替换
if(k >= cnt) cnt ++; // 如果都小于a[i]，重新开一个子序列
}
cout << cnt << endl;
return 0;
}
\(O(nlogn)\)做法：
#include<iostream>
#include<algorithm>
#include<sstream> // 数据量过大的时候用
using namespace std;
const int N = 1010;
int n,f[N],a[N],g[N];
int main()
{
string line;
getline(cin,line);
stringstream ssin(line);
while(ssin >> a[n]) n ++;
// 求最长不升子序列
int res = 0;
for(int i = n-1; i >= 0; i --)
{
f[i] = 1;
for(int j = n-1; j > i;j --)
if(a[j] <= a[i]) f[i] = max(f[i],f[j] + 1);
res = max(f[i],res);
}
cout << res << endl;
// 求最长不升子序列个数
int cnt = 0; // 保存子序列的个数
for(int i = 0; i < n; i ++)
{
// 二分找到替换的位置
int l = 0, r = cnt - 1;
while(l < r)
{
int mid = l + r >> 1;
if(g[mid] >= a[i]) r = mid;
else l = mid + 1;
}
if(g[l] < a[i]) g[cnt ++] = a[i]; // 如果没有二分出来大于当前数a[i]的答案，就再开一个子序列
else g[l] = a[i]; // 二分出答案就替换
}
cout << cnt << endl;
return 0;
}
AcWing 187. 导弹防御系统
原题链接：https://www.acwing.com/problem/content/189/
解剖题目
可以发现是让我们同时求最长上升子序列和最长下降子序列的个数，每一个数只能属于一个子序列中。
所以就不能先求最长上升子序列个数再求最长下降子序列个数。
再看用拦截导弹这一题的贪心能否解决这一题，贪心每次贪心都是有确定情况的，要么加入到某个上升子序列中，要么重新开一个上升子序列。而这个题还需要去考虑下降子序列，只能dfs爆搜+剪枝
如果能退出确定的公式或者递推关系，那么就去dp(等)写，否则就dfs爆搜+剪枝
代码
#include<iostream>
using namespace std;
const int N = 55;
int n,a[N],up[N],down[N];
int ans;
void dfs(int u,int su,int sd) // u枚举到哪个数，su上升子序列的个数，sd下降子序列的个数
{
if(su + sd >= ans) return; // 如果su+sd已经大于ans，那么答案不能再更新变小就直接return
if(u == n)
{
// 枚举到n(结束了)，返回答案=>总子序列个数=su+sd
ans = su + sd;
return;
}
// dfs所有情况
// 情况1:插入到最长不升子序列中去
int k = 0;
while(k < su && up[k] <= a[u]) k ++;
int t = up[k];
up[k] = a[u]; // 替换
if(k >= su) dfs(u+1,su+1,sd); // 如果都小于a[u]就重新开一个子序列
else dfs(u+1,su,sd);
// 恢复现场
up[k] = t;
// 情况2：插入到最长不降子序列中
k = 0;
while(k < sd && down[k] >= a[u]) k ++;
t = down[k];
down[k] = a[u];
if(k >= sd) dfs(u+1,su,sd+1);
else dfs(u+1,su,sd);
down[k] = t;
}
int main()
{
while(cin >> n,n)
{
for(int i = 0; i < n; i ++) cin >> a[i];
ans = n;
dfs(0,0,0);
cout << ans << endl;
}
}
AcWing 272. 最长公共上升子序列
原题链接:https://www.acwing.com/problem/content/274/
解题思路 dp分析
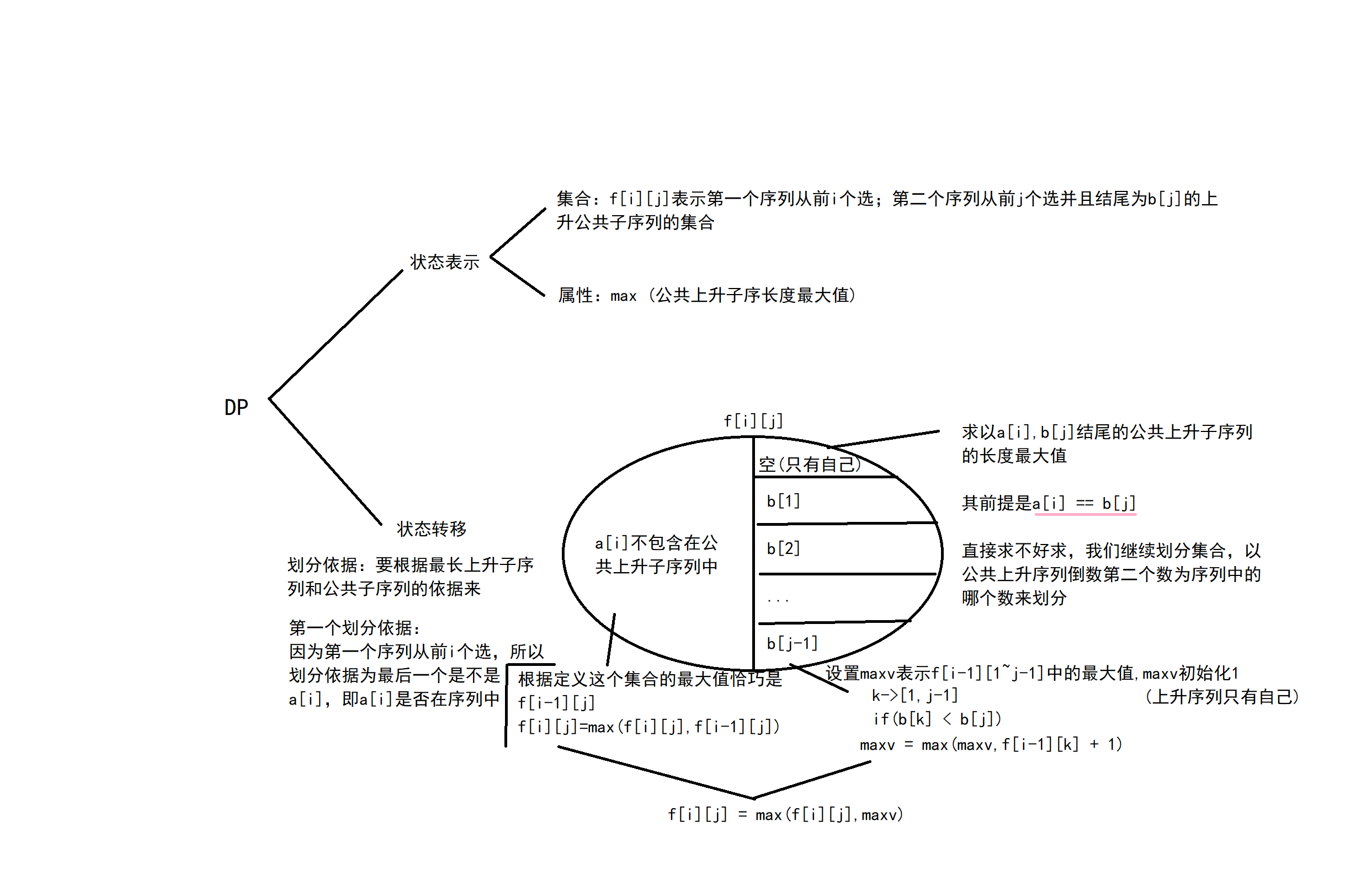
代码 + 优化(保存前缀最大值)
$ O(n^3) $ ，会超时，需要优化
#include<iostream>
using namespace std;
const int N = 3010;
int f[N][N];
int a[N],b[N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n;i ++) cin >> a[i];
for(int i = 1; i <= n;i ++) cin >> b[i];
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n; j ++)
{
f[i][j] = max(f[i][j],f[i-1][j]);
if(a[i] == b[j])
{
int maxv = 1;
for(int k = 1; k < j; k ++)
{
if(b[k] < b[j]) maxv = max(maxv,f[i-1][k]+1);
}
f[i][j] = max(f[i][j],maxv);
}
}
}
int res = 0;
for(int i = 1; i <= n; i ++) res = max(res,f[n][i]);
cout << res;
return 0;
}
a[i] == b[j],第三层循环中每次都计算(b[j] < a[i]) f[i-1][1j]+1的最大值，可以让maxv来保存一个前缀最大值(比如这次j=4,算f[i-1][14]+1的最大值，而maxv已经保存的是f[i-1][1~3]+1的最大值了)，将第三个for(k)循环去掉，减少重复计算。
$ O(n^2) $ 代码
#include<iostream>
using namespace std;
const int N = 3010;
int f[N][N];
int a[N],b[N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n;i ++) cin >> a[i];
for(int i = 1; i <= n;i ++) cin >> b[i];
for(int i = 1; i <= n; i ++)
{
int maxv = 1; // 记录b[1~j]中满足b[j]<a[i]最大值
for(int j = 1; j <= n; j ++)
{
f[i][j] = max(f[i][j],f[i-1][j]);
if(b[j] < a[i]) maxv = max(maxv,f[i-1][j]+1); // b[j]<a[i]时更新f[i-1][1~j]中前缀最大值
if(a[i] == b[j]) f[i][j] = max(f[i][j],maxv); // 当a[i]==b[j]的时候更新f[i][j]
}
}
int res = 0;
for(int i = 1; i <= n; i ++) res = max(res,f[n][i]);
cout << res;
return 0;
}
