acwing240. 食物链 (带权并查集)

acwing240. 食物链

原题链接：https://www.acwing.com/problem/content/242/

带权并查集

思路

维护一个并查集
这个并查集中的每个结点都和根节点有关系(可以吃根节点，与被根节点吃)，因此任意两个结点都可以通过它与根节点的关系而推出这两个结点的关系。

可以用到达根节点的距离来表示和根节点的关系。

结点到达根节点的距离mod3的结果：
余1 ： 可以吃根节点
余2 ： 可以被根节点吃
余0 ： 和根节点同类

此题为了得到结点之间的关系，需要额外维护一个d[x]数组来表示结点x到达其父节点p[x]的距离。(在路径压缩的时候，x的父节点就变成了根节点，d[x]也需要更新成到达根节点的距离)

问题：集合合并的时候(路径压缩，将a集合插入到b集合)，d怎么更新

比如find函数

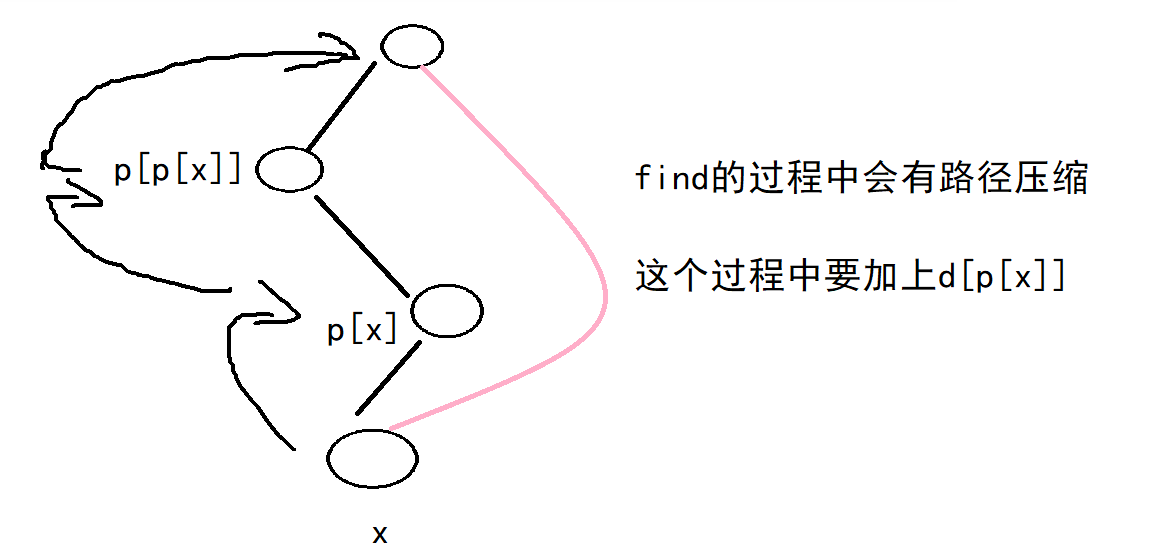
int t = find(p[x]); // 先将祖宗结点保存，find过程中 p[x]已经指向了祖宗结点
d[x] += d[p[x]]; // 他到祖宗结点的距离为它到父节点的距离+父节点到祖宗结点的距离
p[x] = t;

比如x，y是同类，则x、y到达根节点的值是相同的。如果未在同一个集合中
先将px插入到py的节点下

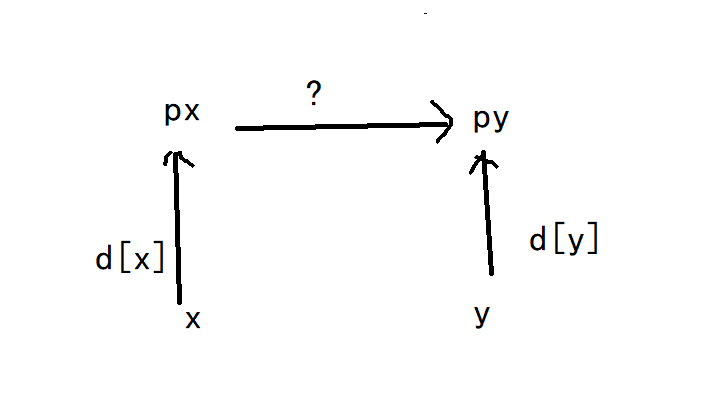
d[x] + ? 同d[y]
所以d[px] = ? = d[y] - d[x]

比如x吃y，则x到达根节点的距离比y到达根节点的距离大1。如果未在同一个集合中就先将px插入到py的下。
d[x] + ? = d[y] + 1
d[px] = ? = d[y] - d[x] + 1

代码

#include<iostream>

using namespace std;

const int N = 50010;

int n,m;
int p[N],d[N];

int find(int x)
{
    if(p[x] != x) // 在路径压缩的时候，要更新d[x]
    {
        int t = find(p[x]); // 先记录成t,然后去d[x]加上d[px]的距离，每一段都要加上
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d %d",&n,&m);
    
    for(int i = 1; i <= n; i ++) p[i] = i;
    
    int res = 0;
    while(m --)
    {
        int t,x,y;
        scanf("%d%d%d",&t,&x,&y);
        
        if(x > n || y > n) res ++;
        else
        {
            int px = find(x),py = find(y); // 先找到x,y的祖宗结点(此时，x，y已经路径压缩，指向了根节点)
            if(t == 1) // 判断xy是否是同类
            {
                if(px == py && (d[x] - d[y]) % 3) res ++; // 在同一个集合里，但是到达根节点距离不同就不是同类
                else if(px != py) // 未在一个集合中，就更新到一个集合里去
                {
                    p[px] = p[py]; // 把x插入的y的集合中去,让px成为py的儿子即可     
                    d[px] = d[y] - d[x];
                }
            }
            else // x 吃 y
            {
                if(px == py && (d[x] - d[y] - 1) % 3) res ++;
                else if(px != py)
                {
                    p[px] = p[y];
                    d[px] = d[y] - d[x] + 1;
                }
            }
        }
        
    }
    
    printf("%d",res);
    
    return 0;
}