容斥原理-acwing890.能被整除的数
学完只想说,实在是妙蛙~
容斥原理
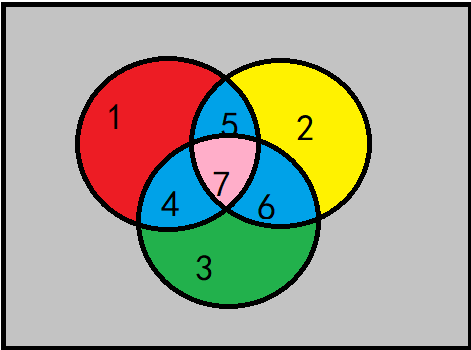
容斥原理:
求并集
如果是两个集合相交的话
可以发现规律 加上一个的,减去两个相交的,加上三个相交的,减去四个相交的,加上五个相交的...
容斥原理时间复杂度
选一个集合的时间(\(S_{1}、S_{2}...\)=>\(C_{n}^{1}\))+选两个集合的时间(\(S_{1}\cap S_{2}\)=>\(C_{n}^{2}\))+选三个集合的时间(\(S_{1}\cap S_{2}\cap S_{3}\)=>\(C_{n}^{3}\))...
即:\(C_{n}^{1}+C_{n}^{2}+C_{n}^{3}+...+C_{n}^{n}\)
不妨添加一个\(C_{n}^{0}\) => \(C_{n}^{0} + C_{n}^{1}+C_{n}^{2}+C_{n}^{3}+...+C_{n}^{n} = 2^n\)(相当于从n个数中挑任意多个数出来,相当于每一个数挑或者不挑)
因此其时间复杂度为\(O(2^n)\)
acwing890.能被整除的数
原题链接:https://www.acwing.com/problem/content/892/
样例解释
n = 10,\(p_1 = 2\),\(p_2 = 3\),求1~10中能满足整除\(p_1\)或\(p_2\)的个数即
2,3,4,6,8,9,10,共7个,即求能整除2的集合\(S_1\)和能整除3的集合\(S_2\)的并集
思路
记\(S_i\)为1~n中能整除\(p_i\)的集合,答案即为所有集合的并集
然后用容斥原理求并集
并不需要求出每个集合具体是什么,我们可以求出每个集合的大小,然后根据容斥原理去做
集合\(S_i\)的大小怎么确定呢?
\(\left \lfloor \frac{n}{p_i} \right \rfloor\) 即为1~n中能整除\(p_i\)的元素的个数
即$\left | S_i \right | = \frac{n}{p_i} $
交集的大小如何确定?
因为所有的\(p_i\)都为质数,因此所有任意两数的乘积就是两数的最小公倍数,因此同理$\left | S_i \bigcap S_j \right |= \frac{n}{p_i * p_j} $
如何使用代码表示每一个集合的状态?
二进制枚举(有点状态压缩的味道),把某些集合选与不选的情况看做一个二进制数,然后枚举所有情况(枚举所有二进制数),m的大小就是集合数量的大小,就是二进制数位数的多少。
然后使用容斥原理。
比如\(m=4\),那么就有情况1101,即选中了集合\(S_1,S_2,S_4\),那么\(S_1 \bigcup S_2 \bigcup S_4\)的大小,即\(\frac{n}{p_1*p_2*p_4}\),选了3个而\((-1)^{3-1} = 1\),因此到这一步应该是res += \(\frac{n}{p_1*p_2*p_4}\)。
ps:这种二进制枚举很常用!~
代码 O(\(m*2^m\))
#include<iostream>
using namespace std;
const int N = 20;
typedef long long LL;
int p[N];
int main()
{
int n,m;
cin >> n >> m;
for(int i = 0; i < m; i ++) cin >> p[i]; // 将m个素数读进来
int res = 0;
for(int i = 1; i < 1 << m; i ++) // 二进制枚举每一种选某些集合不选某些集合的情况
{
int mul = 1,cnt = 0; // mul记录最小公倍数 cnt记录正负号
for(int j = 0; j < m; j ++) // 枚举二进制数的每一位
{
if(i >> j & 1) // 该集合选中
{
if((LL)mul * p[j] > n) // p[j]的范围是1e9,多个p[j]相乘有可能爆int
{
mul = -1;
break;
}
mul *= p[j];
cnt ++;
}
}
if(mul != -1)
{
if(cnt % 2) res += n/mul; // 奇数+,偶数- n/最小公倍数
else res -= n/mul;
}
}
cout << res << endl;
return 0;
}


