acwing889. 满足条件的01序列

acwing889. 满足条件的01序列

原题链接：https://www.acwing.com/problem/content/891/

求组合数
卡特兰数
逆元
快速幂
费马小定理

思路

题目要求一个01串，其任何一个前缀都要保证0的数量不小于1的数量

可以将这个排列转化成一个路径。1表示向上走，0表示向右走

符合排列要求的路径就一定是在x = y这条直线之下(可以到达这条线),即符合要求的路径就一定在y = x + 1这条直线之下

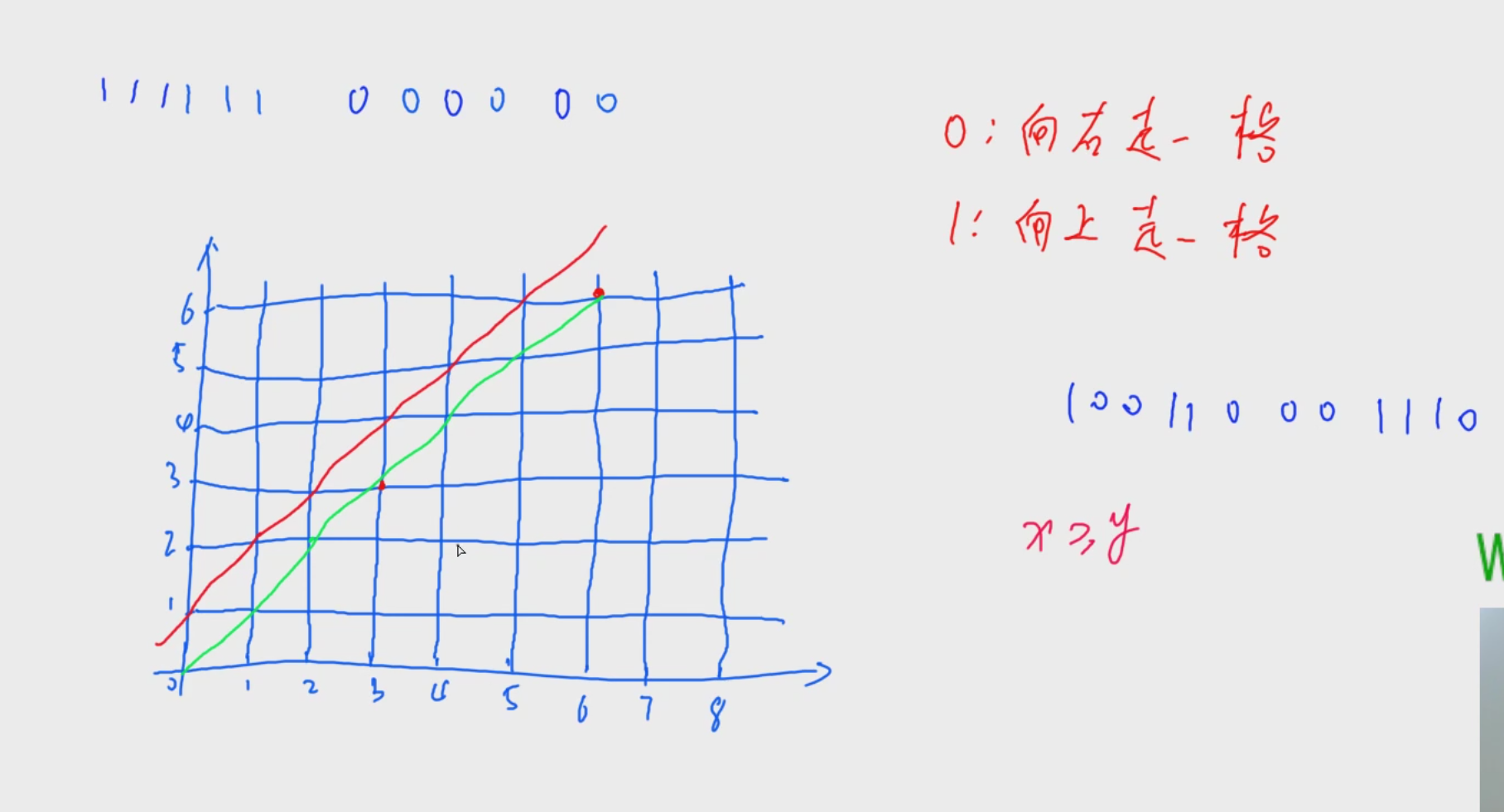
比如样例6个0,6个1

那么答案就是从[0,0]到达[6,6]的路径减去从经过红线的路径\(C_{12}^{6} - 经过红线的路径\)

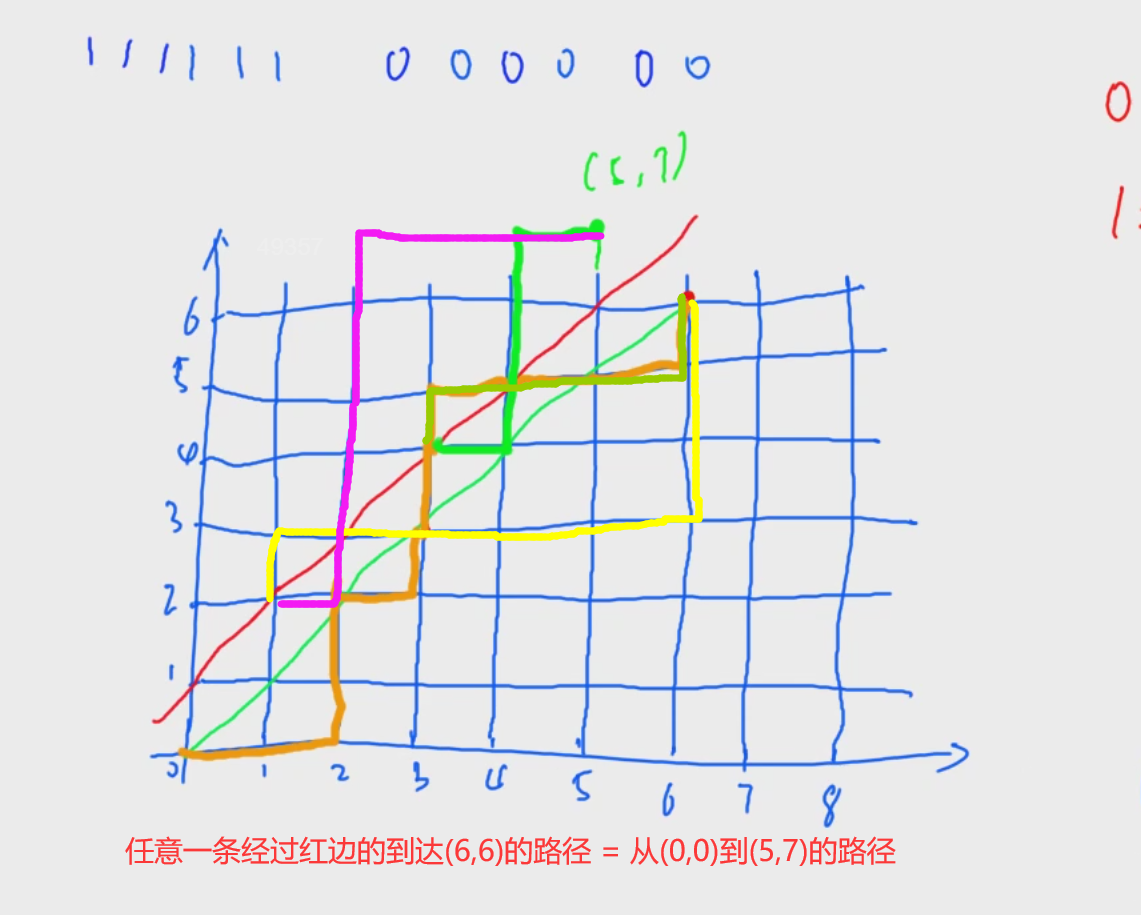
而所有经过红线的路径我们都可以把这个路径以红线做一个轴对称，发现到达[6,6]就是到达[5,7]所有经过红线的路径就是从[0,0]走到[5,7]的所有路径([n,n]经过y=x+1对称得到[n-1,n+1])

所以最后的答案就是\(C_{12}^{6} - C_{12}^{5}\)

即答案为\(C_{2n}^{n} - C_{2n}^{n-1}\)

化简后最终结果为\(\frac{C_{2n}^{n}}{n+1}\)

需要注意的是最后不是直接除以\(n+1\)而是要乘以\(n+1\)模p的逆元：因为是要对最后的结果取模，a / b 是同余 a%p * b的逆元%p 的; 但是不同余 a % p / b %p； 所以需要取模的时候，如果有乘法都要转换成乘法。

代码

#include<iostream>
#include<algorithm>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;// 是质数，求逆元直接用费马小定理

int n;

int qmi(int a,int k,int p)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL) res * a % p;
        a = (LL) a * a % p;
        k >>= 1;
    }
    return res;
}

int main()
{
    cin >> n;
    
    int a = 2 * n,b = n;
    int res = 1;
    for(int i = a; i > a - b; i --) res = (LL) res * i % mod;
    
    for(int i = b; i > 0; i --) res = (LL) res * qmi(i,mod - 2,mod) % mod;
    
    res = (LL) res * qmi(n+1,mod - 2,mod) % mod;
    
    cout << res;
    
    return 0;
}