高斯消元解线性方程组

高斯消元解线性方程

原题链接：https://www.acwing.com/problem/content/885/

初等行列变换操作

\[\left\{\begin{matrix} a_{11}x_{1}+a_{12}x_{2} +...+a_{1n}x_{n} = b_{1} \\ a_{21}x_{1}+a_{22}x_{2} +...+a_{2n}x_{n} = b_{2} \\ . \\ . \\ a_{n1}x_{1}+a_{n2}x_{2} +...+a_{nn}x_{n} = b_{n} \end{matrix}\right. \]

对于一个含n个未知数的方程组，它的解有三种情况：唯一解、无穷多解、无解

将未知数系数和常数项拿出来组成一个矩阵

a11 a12 a13 ... a1n b1
a21 a22 a23 ... a2n b2
...
a31 a32 a33 ... a3n b3

基本的初等行列变换操作有三个：
1.将某一行乘以一个非0的数
2.交换某两行
3.把某一行若干倍加到另一行上去

而经过三种初等行列变换操作之后的结果有三种:
1.完美阶梯型矩阵 唯一解
2.0 = 0 无穷解
3.0 = 非零 无解

高斯消元基本原理$ O(n^3) $

枚举每一列c：
	1.找到这一列中绝对值最大的数所在的行
	2.将该行放到最上面(不是第一行)
	3.将该行的第一个数变成1
	4.将该行下面所有行的第c列数变成0

经过以上变化之后就会得到三种结果(完美阶梯矩阵、0 = 0、0 = 非零)

如果是得到了完美阶梯型矩阵，就求出每一个未知数的值。

回推求值

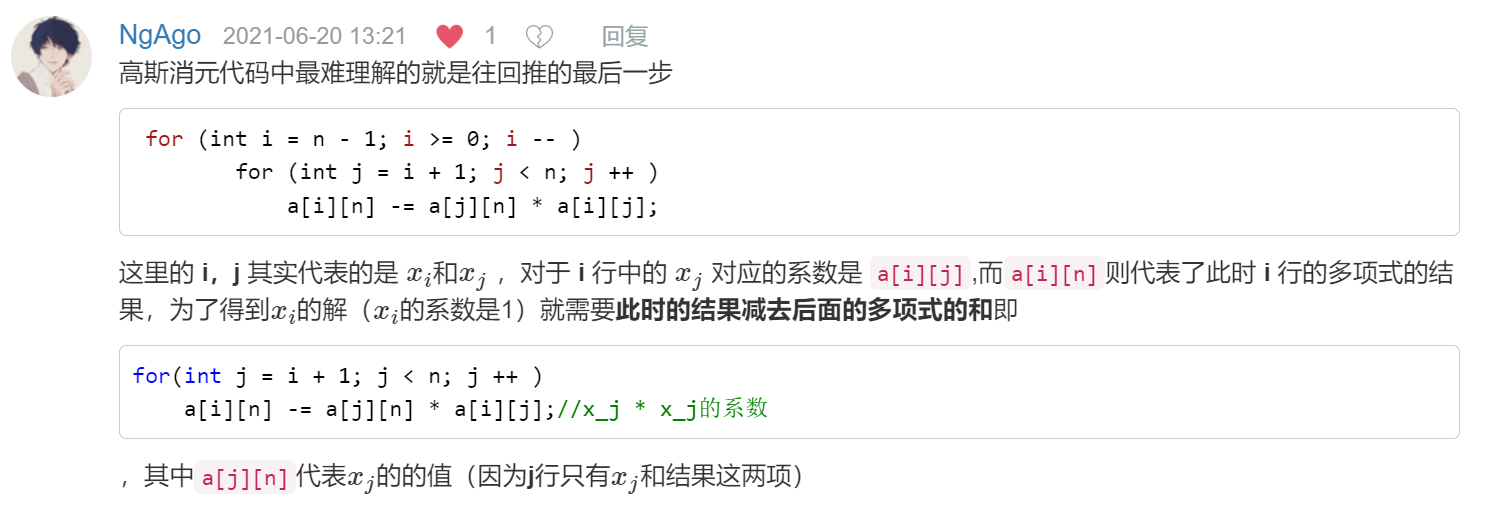
代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>

using namespace std;

const int N = 110;
const double eps = 1e-8;

int n;
double a[N][N];

// void print()
// {
//     for(int i = 0; i < n; i ++)
//     {
//         for(int j = 0; j <= n; j ++)
//         {
//             printf("%.2lf ",a[i][j]);
//         }
//         printf("\n");
//     }
//     printf("\n");
// }

int guass()
{
    int c,r;
    for(c = 0,r = 0; c < n; c ++)
    {
        int t = r;
        for(int i = r; i < n; i ++)
        {
            if(fabs(a[i][c]) > fabs(a[t][c]))t = i;
        }
        
        if(fabs(a[t][c]) < eps) continue; // 如果此列r下都为0就下一列
        
        for(int i = c; i <= n; i ++) swap(a[t][i],a[r][i]); // 将此列绝对值最大所在的行的放到最上面
        
        // print();
        
        // 此时,第r行就是最顶端
        for(int i = n; i >= c; i --) a[r][i] /= a[r][c]; // 将最顶端行首位变成1
        
        // print();
        
        // 此行此列下面的所有数都变成0(用1消)
        for(int i = r + 1; i <n; i ++)
        {
            if(fabs(a[i][c]) > eps) // 如果非0就变成0
            {
                // 第c列减去a[i][c]倍的a[r][c]，后面的也要减去a[i][c]倍的a[r][j]
                for(int j = n; j >= c; j --) a[i][j] -= a[i][c] * a[r][j];
            }
        }
        
        r ++; // 下一行
    }
    
    if(r < n) // 说明不是完美阶梯型
    {
        for(int i = r; i < n; i ++)
        {
            if(fabs(a[i][n]) > eps) return 2; // 如果存在0 = 非零,就返回无解
        }
        return 1; // 否则说明是 0 = 0 返回有无穷解
    }
    
    // 有唯一解就将唯一解保存在a[i][n]中
    for(int i = n - 1; i >= 0; i --) // 完美阶梯型，第i行就会含有i-1个0，即求x[i]就从x[i+1]开始减去
    {
        for(int j = i + 1; j < n; j ++) a[i][n] -= a[i][j] * a[j][n]; // a[i][j]是x[i+1]的系数,a[j][n]是未知数x[i+1]
    }
    
    return 0;
}

int main()
{
    scanf("%d",&n);
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n + 1; j ++)
            scanf("%lf",&a[i][j]);
    
    int t = guass();
    if(t == 2) puts("No solution");
    else if(t == 1) puts("Infinite group solutions");
    else
    {
        for(int i = 0; i < n; i ++)
        {
            if(fabs(a[i][n]) < eps) a[i][n] = 0;
            printf("%.2lf\n",a[i][n]);
        }
    }
    
    return 0;
}