欧拉函数

欧拉函数

acwing873.欧拉函数

定义

欧拉函数\(\varphi (n)\)表示1~n中互质的数的个数

(若n为质数，这\(\varphi (n)\) = n-1)

互质：如果两个数的公约数只有1，则这两个数互质

欧拉函数公式

已知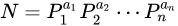

则欧拉函数的公式：

\[\varphi (n) = N(1-\frac{1}{p_1}) (1-\frac{1}{p_2})... (1-\frac{1}{p_k}) \]

证明使用容斥原理，让N减去质数的倍数最后剩下的就是互质的数.

代码

先分解质因数，再用公式求即可

使用公式求的时候不用res*(1 - 1/p)而要使用res / p * (p - 1)，因为c++中是整除 1/p 的结果就会是0

#include<iostream>

using namespace std;

int phi(int x)
{
    int res = x;
    // 试除法分解质因数
    for(int i = 2; i <= x/ i; i ++)
    {
        if(x % i == 0) 
        {
            res = res / i * (i - 1) ;
            while(x % i == 0) x /= i;
        }
    }
    if(x > 1) res = res / x * (x - 1); // 不要忘记漏乘，因为x有可能存在一个大于sqrt(x)的质因子
    
    return res ;
}


int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int x;
        cin >> x;
        cout << phi(x) << endl;
    }
    
    return 0;
}

线性筛法求欧拉函数

acwing874.线性筛法求欧拉函数

这种一般都是求1~n中所有数的欧拉函数值的和

这时我们要使用线性筛法筛质数去改写求欧拉函数，这样时间复杂度为O(n)

质数i的欧拉函数即为phi[i] = i - 1：1 ~ i−1 中i−1均与i互质，共i−1个。

phi[primes[j] * i]分为两种情况：
① i % primes[j] == 0时：
	primes[j]是i的最小质因子，也是primes[j] * i的最小质因子，因此
	1 - 1 / primes[j]这一项在phi[i]中计算过了，只需将基数N修正为p
	rimes[j]倍，最终结果为phi[i] * primes[j]。
② i % primes[j] != 0：
	primes[j]不是i的质因子，只是primes[j] * i的最小质因子，因此不
	仅需要将基数N修正为primes[j]倍，还需要补上1 - 1 / primes[j]这
	一项，因此最终结果phi[i] * (primes[j] - 1)。
	
	也可以这么想，primes[j]为质数，因此它有primes[j]-1个互质的数，
	而i有phis[i]个，并且primes[j]不是i的质因子，所以结果就相乘，是
	phi[i] * (primes[j] - 1)

代码

#include<iostream>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int primes[N],cnt;
int phis[N];
bool st[N];

void get_phis(int n)
{
    phis[1] = 1;
    for(int i = 2; i <= n; i ++)
    {
        if(!st[i])
        {
            phis[i] = i - 1; // i为最小质因子，phi[i] = i - 1
            primes[cnt ++] = i;
        }
        for(int j = 0; primes[j] * i <= n; j ++)
        {
            st[primes[j] * i] = true; // 将这个合数筛去
            if(i % primes[j] == 0) 
            {
                phis[primes[j] * i] = phis[i] * primes[j]; // primes[j]为i最小质因子，也为primes[j]*i的最小质因子，phis[i]中已经包括了(1-1/primes[j])，只需将N修正为原来的primes[j]倍即可
                break;
            }
            phis[primes[j] * i] = phis[i] * (primes[j] - 1); // primes[j]不是i质因子,不仅要将基数N改为原来的primes[j]倍，还要乘上(1 - 1/primes[j])，最终结果为phis[i] * (primes[j] - 1)
        }
    }
}

int main()
{
    int n;
    cin >> n;
    
    get_phis(n);
    
    LL res = 0;
    for(int i = 1; i <= n; i ++) res += phis[i];
    
    cout << res << endl;
    
    return 0;
}